改訂新版 世界大百科事典 「非線形力学」の意味・わかりやすい解説
非線形力学 (ひせんけいりきがく)
nonlinear dynamics
一般に,事象が一定の法則に従って時間的に推移するとき,これを定量的に時間の関数として表す課題を広い意味で力学と呼ぶことにし,その法則が,事象を表す変数x(一つとは限らないのでベクトルで表す)の時間tに関する常微分方程式,

の形で示される場合を考える。fの添字μは外的な条件によって変化しうるパラメーターを意味し,方程式(1)の解がその変化によって受ける変動のようすを調べるのに用いられる。fμ(x)がxの一次関数ならばこの力学系は線形であるといい,その解は簡単に求まるが,結果は力学系の示す性質として内容に乏しい。このような線形力学系の枠をはずした非線形方程式(1)の研究は,1930年代以後しだいに活発となり,70年代に入って応用数学,物理学,工学,生物学などの各分野にわたり世界的な規模で発展を見るに至ったのである。したがって,初めに用いた〈事象〉の語も,自然現象のみならず,社会・経済現象をも含むものである。また,時間を表すtが連続変数でない場合,差分型の方程式,
xn+1=fμ(xn) (n=1,2,3,……) ……(2)
も興味ある事象の説明に役だつことが明らかとなり,このような不連続な事象の推移(写像と呼ばれる)も広い意味での力学とみなされている。したがって以上を総称し,非線形関数fにより,法則が(1),(2)の形で示される事象の推移を一般に非線形力学と呼ぶ。
線形・非線形力学の代表例
以下,実例によって特徴を示そう。最初のものは線形の代表,次の三つは保存型(ハミルトン系)非線形力学の例,最後の三つは散逸型を含むそれ以外の例である。また以下では,例えばẋとかけば,これは時間微分dx/dtを表すことにする(ẍ=d2x/dt2)。
調和振動子
ẋ=p,ṗ=-ω2x
質点の静止点からの変位x(t)がつねにxに比例する力によって引き戻される場合,質点は理想的な振動,すなわちAcosωt+Bsinωtのように表される運動を行う。これはニュートンの運動方程式mẍ=-Fx(mは質量Fは力で定数;ω=\(\sqrt{F/m}\))がxに関し線形で,調和振動と呼ばれるものである。これを上掲の形に表すためにはハミルトン関数H(p,x)=p2/2+ω2x2/2(簡単のためm=1とする。またpは運動量)から導かれるハミルトンの運動方程式に従えばよい。二次元相平面(p,x)上で運動を表現するならば,図1のように原点を中心とする楕円群(異なる楕円は異なるエネルギー値Eに対応)によって表され,相平面はすべてこの型の周期運動を表す楕円によりうずめつくされる。すなわち,1回の調和振動は点(p(t),x(t))が一つの楕円を一周する周期運動に相当し,その周期Tは,作用積分,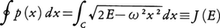 より,
より,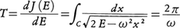 のように計算され,すべての楕円について共通である。
のように計算され,すべての楕円について共通である。
重力振子
θ=p,ṗ=-ω2sinθ
長さlの糸の一端におもりをつけ他の一端を固定して重力下で振らせるときの運動は,糸が垂直に静止した状態から測った角度θに対するニュートン方程式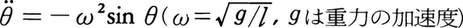 から求められる。これをハミルトン関数H=p2/2+ω2(1-cosθ)から導いたものが上掲の正準運動方程式であり,調和振動子と比較してもっとも簡単な非線形性を備えた振動子とみることができる。その特徴は同様に相平面(p,θ)上での等エネルギー線(図2)の構造から調べることができる。調和振動子と同様原点θ=0,p=0は振子の静止状態(E=0)に相当するが,今度の場合すべての等エネルギー線は正準座標θの2πを周期とする周期関数であり,運動は2種類に分類される。すなわち,エネルギーEを0から増大させるとき,Eの小さな範囲では相平面上軌道は閉じていて調和振動に近い運動を表すのに対し,十分大きいEに対しては等エネルギー線は-∞から∞まで伸びた閉じない軌道による周期運動を表す。この後者の運動は糸の固定位置を中心とする振子の回転運動に相当している。この2種類の運動は他のもう1組の静止の点H(θ=±π,±3π,……;p=0)を通る2本の線によって分離されているので,この2線は分離帯と呼ばれている。また,点Hは振子のおもりが直上に静止した状態であって,不安定平衡点または振動の安定平衡点である原点の楕円点elliptic pointに対して双曲点と呼ばれている。運動の周期はEの関数として一定ではない。
から求められる。これをハミルトン関数H=p2/2+ω2(1-cosθ)から導いたものが上掲の正準運動方程式であり,調和振動子と比較してもっとも簡単な非線形性を備えた振動子とみることができる。その特徴は同様に相平面(p,θ)上での等エネルギー線(図2)の構造から調べることができる。調和振動子と同様原点θ=0,p=0は振子の静止状態(E=0)に相当するが,今度の場合すべての等エネルギー線は正準座標θの2πを周期とする周期関数であり,運動は2種類に分類される。すなわち,エネルギーEを0から増大させるとき,Eの小さな範囲では相平面上軌道は閉じていて調和振動に近い運動を表すのに対し,十分大きいEに対しては等エネルギー線は-∞から∞まで伸びた閉じない軌道による周期運動を表す。この後者の運動は糸の固定位置を中心とする振子の回転運動に相当している。この2種類の運動は他のもう1組の静止の点H(θ=±π,±3π,……;p=0)を通る2本の線によって分離されているので,この2線は分離帯と呼ばれている。また,点Hは振子のおもりが直上に静止した状態であって,不安定平衡点または振動の安定平衡点である原点の楕円点elliptic pointに対して双曲点と呼ばれている。運動の周期はEの関数として一定ではない。
ケプラー運動
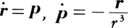
惑星運動やクーロン力によって束縛された荷電粒子(電子)の運動として古くからその解が知られた基本的な非線形力学系であり,ハミルトン関数H=p2/2-1/rから導かれる自由度3の系である。ポテンシャルが座標ベクトルrの絶対値 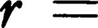
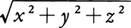 だけの関数であるため,エネルギー積分H=E以外に角運動量の積分(r×p)2=L2およびr×pの一成分(r×p)z=Lzが独立な運動の定数を形成している。さらにポテンシャルU(r)=-1/rの特殊性から,次のように定義されるベクトルA=p×L-r/rが運動の定数であることが知られていて,レンツベクトルと呼ばれている。軌道r(t)はLに垂直な平面内で円錐曲線を描き,レンツベクトルAの大きさがこの円錐曲線の離心率をきめている。
だけの関数であるため,エネルギー積分H=E以外に角運動量の積分(r×p)2=L2およびr×pの一成分(r×p)z=Lzが独立な運動の定数を形成している。さらにポテンシャルU(r)=-1/rの特殊性から,次のように定義されるベクトルA=p×L-r/rが運動の定数であることが知られていて,レンツベクトルと呼ばれている。軌道r(t)はLに垂直な平面内で円錐曲線を描き,レンツベクトルAの大きさがこの円錐曲線の離心率をきめている。
すなわち,
|A|=1 放物線軌道(E=0,すい星の運動)
|A|>1 双曲線軌道(E>0,ラザフォード散乱)
楕円軌道の場合,軌道を一周する運動の周期は,
T=2πL3(1-|A|2)⁻3/2=2π(-2E)3/2
で与えられ,惑星運動に関するケプラーの第3法則を表すものである。
非線形結合振動子
さまざまな実例中以下の2例がよく知られている。
(1)ヘノン=ハイレス系
q1=p1,ṗ1=-q1-2q1q2
q2=p2,ṗ2=-q2-q12+q22 ……(3)
(2)戸田格子
qn=pn,ṗn=exp{-(qn-qn-1)}-exp{-(qn+1-qn)} (n=1,2,……,N;N+i≡i) ……(4)
これまでの例は運動方程式の解が求積法によって求まる場合(可積分系と呼ばれる)であった。自由度が2以上のハミルトン力学系ではいつでもそのように解けるとは限らない。例えば三次元空間内で回転対称性をもつ物体の運動(自由度3)では,エネルギー積分と角運動量積分という二つの運動の定数(積分)があり,もう一つそのような定数が見つかれば求積法により解かれるので,多くの例でこの積分,すなわち第三積分が探し求められた。ケプラー運動のように球対称のポテンシャル運動はその典型である。もし第三積分が存在しない場合には,四次元相空間内で一つの初期値から出発する軌道は,相空間を密にうずめることが予想され,したがってそのような軌道のふるまいを調べることにより第三積分の存否を確かめることができると予想された。ヘノン=ハイレス系は銀河のモデルをたてるのにこの予想を確かめる必要性から考えられたもので(1964),右辺の二次の力がない場合は単純な線形振動子となって第三積分が存在するのに対し,この非線形項のためにそれは失われることになる。ヘノンとハイレスはこのことを示すのに(3)の解を数値的に求め,ポアンカレ写像の方法(後述)を初めて適用したのである。その結果わかったたいせつな事実は,どんなエネルギー値に対しても第三積分が存在しないのではなく,低エネルギーの一定範囲では第三積分を示す規則性が確かめられたことで,その後の非線形力学系研究の重要な端緒となった。
これに対し,戸田格子は求積法によって解が求められる非線形結合振動子の顕著な例であって,1967年戸田盛和によって発見された。運動方程式(4)の右辺の力は,隣接振動子の変位差を指数関数的に含む非線形性を示し,これを展開して最低次の項を残したものは一次元調和格子振動となる。これはもちろん可積分系であり,各振動子の変位のフーリエ分解によって固有モードが得られ,さらに波数の連続体近似によって線形波動方程式,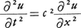 で表されることになる。
で表されることになる。
一方,一次元非線形波動を示す典型として古くからKdV(コルトベーグ=ド・フリース)方程式,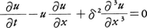 が知られていたが,やはり1960年代の終りにその局在進行波解が発見され,ソリトンsolitonと名づけられた。戸田は(4)を展開せずに連続体近似するとそれがKdV方程式となることを示し,また(4)の素解の中にソリトンに相当するものを発見した。これらの結果,戸田格子は非線形力学の一大研究分野となった。
が知られていたが,やはり1960年代の終りにその局在進行波解が発見され,ソリトンsolitonと名づけられた。戸田は(4)を展開せずに連続体近似するとそれがKdV方程式となることを示し,また(4)の素解の中にソリトンに相当するものを発見した。これらの結果,戸田格子は非線形力学の一大研究分野となった。
ローレンツ系
Ẋ=-σX+σY
Ẏ=-XZ+rX-Y
Ż=XY-bZ
ハミルトン力学系が相空間の体積保存性を示すのに対し,力学変数の空間の任意領域の体積が時間とともにしだいに0に収縮する力学系を一般に散逸系と呼び,その代表例として1963年にE.N.ローレンツによって提案された上掲の運動方程式(ローレンツ方程式)を考える。この右辺は,変数X,Y,Zについて二次の非線形項を含む点でヘノン=ハイレス系と似ているが,一次の部分に以下のような意味での体積収縮性が含まれている点で異なる。すなわち時間とともに変化する軌道x(t)を一般に〈流れ〉と呼ぶならば,ẋ(t)は流れの速度場であり,変数空間の体積変化率は,速度場ẋ(t)の発散∇ẋ(t)で与えられるので,∇ẋ(t)<0が散逸性の条件を表す。ローレンツ方程式は,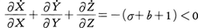 で,確かにこの条件を満たしている。ただし,σ,bは正の定数である。ほかにもう一つの定数rが含まれているが,これは可変であって,方程式(1)のx(t)に付す添字μに相当している。これを正の範囲で変化させると方程式の解の漸近的性質にきわめて顕著な特徴が現れ,乱流現象を説明する一つのモデルとなることをローレンツが初めて指摘した(1963)。すなわち,上下2層の平板に収められた流体を下部から熱し,上下層間の温度こう配を高めていくときに熱対流が生じ,さらに高めると乱流状態が発生するが,このことを記述するのは流体物理学の重要課題の一つである。ローレンツは無限自由度の基本方程式を扱う困難を避けて,速度ポテンシャルと温度差とをフーリエ分解して得られる最重要な3成分だけを取り,他を捨てる近似の結果,上掲の方程式に到達した。一般に散逸系では速度場の各成分をすべて0とする点(不動点と呼ばれる)がいくつかあり,解の漸近的挙動は各不動点における解の安定性に支配される。線形散逸系ではただ一つの安定な不動点があって,解はつねにこの不動点に向かい,最後に静止するわけであるが,非線形性が入ると,漸近解として定常的な周期運動や非周期運動が現れうることをローレンツが初めて指摘した。ローレンツ方程式の非線形性はごく簡単なものであるが,それにもかかわらず可変パラメーターr(レーリー数に相当)を正の小さな値から増大させていくと,不動点(X=Y=Z=0)が不安定となり,ついには非周期運動が現れることを見いだし,ローレンツはこれをもって乱流状態を説明するものとしたのである。のち,このような解はカオスchaosと呼ばれて非線形力学系に普遍的な現象であることがわかってきた。
で,確かにこの条件を満たしている。ただし,σ,bは正の定数である。ほかにもう一つの定数rが含まれているが,これは可変であって,方程式(1)のx(t)に付す添字μに相当している。これを正の範囲で変化させると方程式の解の漸近的性質にきわめて顕著な特徴が現れ,乱流現象を説明する一つのモデルとなることをローレンツが初めて指摘した(1963)。すなわち,上下2層の平板に収められた流体を下部から熱し,上下層間の温度こう配を高めていくときに熱対流が生じ,さらに高めると乱流状態が発生するが,このことを記述するのは流体物理学の重要課題の一つである。ローレンツは無限自由度の基本方程式を扱う困難を避けて,速度ポテンシャルと温度差とをフーリエ分解して得られる最重要な3成分だけを取り,他を捨てる近似の結果,上掲の方程式に到達した。一般に散逸系では速度場の各成分をすべて0とする点(不動点と呼ばれる)がいくつかあり,解の漸近的挙動は各不動点における解の安定性に支配される。線形散逸系ではただ一つの安定な不動点があって,解はつねにこの不動点に向かい,最後に静止するわけであるが,非線形性が入ると,漸近解として定常的な周期運動や非周期運動が現れうることをローレンツが初めて指摘した。ローレンツ方程式の非線形性はごく簡単なものであるが,それにもかかわらず可変パラメーターr(レーリー数に相当)を正の小さな値から増大させていくと,不動点(X=Y=Z=0)が不安定となり,ついには非周期運動が現れることを見いだし,ローレンツはこれをもって乱流状態を説明するものとしたのである。のち,このような解はカオスchaosと呼ばれて非線形力学系に普遍的な現象であることがわかってきた。
ポピュレーション・ダイナミクスpopulation dynamics
一種または数種の集団X,Y,……において,各集団を構成する個体の数が環境の作用や集団相互の交渉により変化する場合,そのような個体数の消長を調べる方程式は非線形力学方程式となり,化学反応論,集団生物学,社会学などに役だっている。代表例として二つあげる。
(1)ロジスティック方程式
(2)ボルテラ=ロトカ方程式
ẋ=(-α+λy)x
ẏ=(β-μx)y ……(6)
なお,この方程式においてx,y,t以外の文字はすべて正の定数を表す。一般にこれらの方程式は個体数の増殖を表すためにたてられたものであり,線形方程式を考察すると,例えばẋ=εxからただちにわかるとおり,増殖は指数関数的(x(t)∝eεt)であり,散逸の逆現象を示す。多くの場合,時間の経過とともに増殖は頭うちとなり,個体の無限の増加は起こらないのがふつうであるから,そのような抑制効果を生ずる原因としての非線形項が不可欠である。1種類の集団に関するモデル(5)の場合では,二次の非線形項-εx2/Kが抑制効果(密度効果と呼ばれる)を与えていて,t→∞で個体数xは一定値Kに飽和する。この値は(5)の右辺が0となる不動点の一つであり,安定な不動点である。2種類以上の集団の場合にも,このような安定な不動点に向かって解が接近していくケースがもっともふつうにみられるポピュレーション・ダイナミクスの型であり,図3-aに示す。これに対し,ある種のポピュレーション・ダイナミクスでは,解の描く曲線がt→∞で1点に収束せず,一定の閉曲線に向かい,このまわりを定常的にめぐる場合が生ずる。この閉曲線は極限サイクルと呼ばれ,光の発振現象や化学反応などに例をみることができる。
次の方程式は三次の非線形性によって極限サイクルが生ずる例である。
ẋ=-y+x(1-x2-y2)
ẏ=x+y(1-x2-y2)
それは,x=rcosφ,y=rsinφという極座標表示で調べれば容易にわかるとおり,x-y平面上の単位円が極限サイクルとなって,この円の内部の任意の点から出発した解は,角速度1で回転しながらついにはこの円周上を定常的に回転するようになる(図3-b)。これはレーザー発振のモデルであって,r2が発振光のフォトン数,φ=ωtのω(上の方程式ではω=1)が発振周波数に相当している。図3-cはボルテラ=ロトカ方程式の解が描く閉曲線であるが,これは極限サイクルではない。元来このモデルは2種の生物X,Yがあって,YはXの餌であり,XがいなければYは増殖するがXのために食われて頭うちとなるという状況を説明するために考えられた。Xを捕食者という。Xは捕食によってのみ増殖するので,Yが減少するとXもまた増殖できなくなり,おくれて減少を示すが,その結果は再びYの増大となるので,X(t),Y(t)は位相がずれた周期的曲線となり,X-Y平面上閉曲線を描くことになる。しかし時間によらない運動の定数があるため,閉曲線は初期値に依存して定まるのである。
ロジスティック定差方程式
Xn+1=aXn(1-Xn) (n=0,1,2,……)
前出のロジスティック方程式(5)において,時間tが連続ではない変数の場合,すなわち区間⊿tで⊿t,2⊿t,……,n⊿tのような離散値を取るものとするなら,それに対する変数xnの時間微分ẋを差分(xn+1-xn)/⊿tで置き換えて,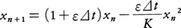 を得る。そこでXn≡ε⊿txn/K(1+ε⊿t),a=1+ε⊿tとして上掲の方程式に達する。このような差分方程式を用いるポピュレーション・ダイナミクスは,例えばセミのように一世代と次の世代との間に空白期間があるような生物の個体数消長をモデル化する必要性から生まれた。微分型の場合のロジスティック方程式は単純であるから,そこから導かれる結論はひととおりでしかない。それが差分型で見直すことにより,パラメーターaの値の変化に対しきわめて多様な解が得られることがわかって注目され,新しい研究に発展したものである。1変数の場合,一般的に,
を得る。そこでXn≡ε⊿txn/K(1+ε⊿t),a=1+ε⊿tとして上掲の方程式に達する。このような差分方程式を用いるポピュレーション・ダイナミクスは,例えばセミのように一世代と次の世代との間に空白期間があるような生物の個体数消長をモデル化する必要性から生まれた。微分型の場合のロジスティック方程式は単純であるから,そこから導かれる結論はひととおりでしかない。それが差分型で見直すことにより,パラメーターaの値の変化に対しきわめて多様な解が得られることがわかって注目され,新しい研究に発展したものである。1変数の場合,一般的に,
Xn+1=fa(Xn)
と書かれるが(ロジスティック模型ではfa(x)=ax(1-x)),これは連続変数Xnのある区間を他の変数Xn+1の同じ区間に移す写像と理解することができる。そして初期値X0から出発してXnに達するのはこの写像をn回繰り返すことである。このとき,Xnのnに対する変化のようすを調べるのに,しばしば図4で例示する作図法(ロジスティックマップと呼ばれる)が用いられる。これは横軸がXnの区間,縦軸が写像によって得られるXn+1の対応区間を表し,その正方形の内部に写像関数のグラフを描くことにより,Xnの1点がXn+1のどの点に写像されるかを見ることができる。また,この対応点を通って横軸に平行線を引き,45度の直線Xn+1=Xnとの交点をみることにより,繰返しの写像点の値を定めることができるので,この作図を次々と行ってXnのnに対する変化のようすがわかる。ロジスティック模型では写像関数fa(0<a≦4)は下に開いた放物線で,区間[0,1]がそれにより同じ[0,1]に写像され,aが1から増大するとき次のa~dで示すような異なる型の解が得られる。図4において放物線と45度の直線との交点はX=fa(X)を満たし,写像の不動点と呼ばれるが,この点の不安定化によって特殊な解が現れるのである。
a. 1<a≦2 安定不動点に向かう単調増加解(微分型の場合に相当)
b. 2<a≦3 いったん増大した後,安定不動点に向かう単調減少解
c. 3<a≦1+\(\sqrt{6}\) 不安定不動点近傍から出発し周期2で振動する周期解に向かう
d. 区間[0,1]のほとんどの点から出発しても解は収束せず,[0,1]区間の至るところをくまなくめぐる
この最後の型は一次元写像のカオスと呼ばれている。
可積分・非可積分力学系
多自由度のハミルトン運動方程式を解くのに運動の積分定数の存在が役だつことは明らかだが,これに関し次のリウビルの定理がある。すなわち,〈自由度fのハミルトニアンH(p1,……,pf;q1,……,qf)の系において,もしf個の互いに独立で包合の関係にある積分{Fi(p,q)(i=1,……,f)}が存在すれば,解を時間の関数として表すことができる〉というものである。ここで互いに独立で包合の関係にある{Fi}とは,どのFiも他のFによって表されることなく,しかもポアソン括弧{Fi,Fj}=0となることを意味している。あるハミルトン力学系がこの性質を備えているとき,これを可積分系,そうでないときは非可積分系という。例えば三次元空間における質点の中心力による運動(ケプラー運動はその代表例)では,エネルギー積分H(p,q)=E,角運動量Lの一成分,およびL2の3積分がそのような積分に該当するので,可積分系である(Lの2成分は互いに独立であるが包合でない({Li,Lj}≠0)ので該当しない)。このような場合,Pi=Fi(p,q)を新しい正準運動量とする正準変換を行うことができて,Piに対する一般化座標Qiは,Qi=νit(νiは定数)のように積分されるので,Pi=一定とともに逆変換によって元に戻してやれば解が求められたことになる。中心力の場合,このような変換は,直交座標から極座標に移って三つの独立な一自由度系としてから行うことができるので,とくに変数分離系と呼ばれる。したがって変数分離系でなくても可積分系である場合があり,また一般に非可積分系だからといって軌道が求められないわけではない。戸田格子(4)に対し,N個の独立,包合の積分が発見され(1973),その結果,戸田格子は可積分非線形力学系の顕著な例であることが確立した。
ポアンカレ写像
3変数以上の力学系の軌道を調べるためJ.H.ポアンカレによって考案された方法で,一定初期値の軌道が1平面を何回も過ぎる点を記録することにより,その力学系運動の規則性,不規則性が探索される。平面はこの力学系軌道の切断面と呼ばれ,それぞれの場合に適切なものがえらばれる。例として自由度2のハミルトン系を考えると,一般にエネルギー積分のため軌道は四次元相空間(p1,q1,p2,q2)の中の三次超曲面上にあるが,さらにもう一つの積分があれば,そのなすもう一つの曲面との交わりの二次元曲面に収められる。したがって,同一軌道のある平面(例えばq1-p1面)を切断面とするポアンカレ写像は,規則的な閉曲線を形成する。これに反し,他の積分が存在しなければ,写像点は切断面上の一定範囲にきわめて不規則に分布することになるので,この方法により第三積分の存否がテストされるわけである。図5-a,bはヘノンとハイレスによって初めて示された非線形結合振動子(3)の切断面q1=0に関するポアンカレ写像で,すべてのエネルギー値Eに対しては第三積分は存在しないが,Eの十分小さな値に対しては存在していることが実証された。図5-bで見られる部分的に散らばった点が不規則運動を示しており,ここでは第三積分が失われている。Eの値をさらに増加させるとこのような写像点の不規則分布は切断面全体に広がり,運動はカオスとなる。比較のため図5-cに3質点からなる戸田格子(4)のポアンカレ写像を示す。この場合はEをどのように大きくしても写像点の不規則分布は現れず,この力学系が完全な可積分系であることを暗示する(事実,(4)の可積分性の証明はこのような数値実験の結果促進された)。
カオスchaos
前述の例の二,三ですでに見たように,微分方程式(1)や定差方程式(2)の解である非線形力学系の特徴として,個々の軌道を解析的に追跡することが不可能な不規則運動の出現することが明らかとなり,これらを総称してカオスと呼ぶのが例となっている。元来,方程式(1)または(2)ではある時刻における変数xの値が与えられたとき,それ以後の時刻でのxは一義的に定まるはずで,〈決定論的力学〉と呼ばれるものである。これに対し,実在するランダム力(ノイズ)によって駆動される力学系で軌道が確率的にしか定められないものもあり,〈確率過程〉と呼ばれているが,カオスの現象は決定論的力学の中にあたかも外見上確率過程と同じ様相を呈するものがあるということを意味し,自然法則の決定性と蓋然性との橋渡しをしているという意味で,現代非線形力学の一つの中心課題となっている。図5-bに見られるヘノン=ハイレス系のポアンカレ写像の不規則点は保存力学系カオスの典型例である。この例からも知られるとおり,カオスの起因として解軌道のもつ不安定性があげられる。すなわち規則運動の範囲内のポアンカレ写像(図5-a)に見られる一つの交差点には,必ずそれを通る安定な曲線群と不安定な曲線群とが分離帯を境として共存していて,後者に属する2曲線は,初め十分接近していても指数関数的に遠ざかっていくことになり,確率的なふるまいの原因となる。したがってカオスはこの付近から出現するのである。また,方程式(1)が散逸系を表す場合,長時間後の系の状態点 xはアトラクターattractorと呼ばれ,簡単な場合はfμ(x)=0とする不動点または極限サイクルがこれに相当しているが,カオスを呈する散逸系では漸近軌道が一定の領域をくまなくおおうような様相を示すためストレンジ・アトラクターstrange attractorと名づけられた。ローレンツ系はストレンジ・アトラクターをもつ散逸系の典型例であり,fμ(x)の不動点がパラメーターμの変化に対して次々と不安定化することにより発生する。それは分岐bifurcationと呼ばれる。図6では,より明りょうなモデル(レスラー,1976)によってその様相を示す。ストレンジ・アトラクター上のカオス・ダイナミクスは,流体における乱流の発生,化学反応,非線形媒質中の透過レーザー光,非線形核磁気共鳴,強磁性・反強磁性共鳴など多くの自然現象の中から実験結果として観測されるようになった。
執筆者:長谷川 洋
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報

