精選版 日本国語大辞典 「ヒルベルト空間」の意味・読み・例文・類語
日本大百科全書(ニッポニカ) 「ヒルベルト空間」の意味・わかりやすい解説
ヒルベルト空間
ひるべるとくうかん
Hilbert space
1900年ころ、ドイツの数学者ヒルベルトは積分方程式を解くのに、未知関数をフーリエ級数に展開すると、フーリエ係数についての無限連立一次方程式となることから、無限数列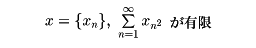
の全体を(l2)で表し、x={xn}∈(l2)とy={yn}∈(l2)との内積を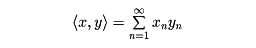
で定義すると、(l2)はp次元ユークリッド空間において次元pを無限大にした極限と考えられるので、幾何学的な直観が使えることに気づき、空間(l2)の性質を調べた。これがのちにヒルベルト空間とよばれるものである(他のヒルベルト空間の例L2(a,b)については「関数解析」の項参照)。
現在ではヒルベルト空間はもっと抽象的に定義される。実数または複素数を係数とするベクトル空間Hで、x,y∈Hに対し、内積として複素数〈x,y〉(実数係数のときは実数)が定義され、a、bを係数とすると、
(1) 〈x,x〉≧0, 〈x,x〉=0ならばx=0
(2) 〈y,x〉=〈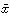 ,
,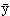 〉 (āはaの共役複素数)
〉 (āはaの共役複素数)
(3) 〈ax+by,z〉=a〈x,z〉+b〈y,z〉
を満足する。このとき、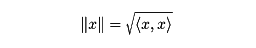
と置くと‖ ‖はHのノルムになる。このノルムから導かれた距離に関し完備となるとき、Hをヒルベルト空間という。明らかにヒルベルト空間はバナッハ空間である。
x,y∈Hに対して〈x,y〉=0ならば、xとyは直交するという。すると、ヒルベルト空間には互いに直交する要素の列{xn;‖xn‖=1}が存在し、Hの任意の要素xは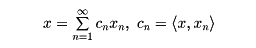
の形に展開できる。このとき、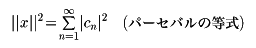
が成立する。
よって、xは{cn}∈(l2)と一対一の対応がつき、しかもノルムを保存するから、Hの代りに(l2)で考えてもよい。
ヒルベルト空間H上の有界線形汎(はん)関数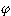 を考えると、Hの要素
を考えると、Hの要素 が決まり、
が決まり、
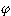 (x)=〈x,
(x)=〈x, 〉
〉
と内積で表される(リースの定理)。よってHの共役空間はH自身であると考えることもできる。このように考えると、Hの有界線形作用素Tの共役作用素T*もHに作用することになり、任意のx,y∈Hに対し、
〈Tx,y〉=〈x,T*y〉
の関係が成り立つものとしてよい。
ヒルベルト空間Hの上の有界線形作用素の全体をMで表すと、T,S∈Mに対し、和S+Tも、スカラー倍aTもMに属し、さらに
(ST)(x)=S(T(x)), x∈H
によって積を定義すると、ST∈Mとなり、
‖ST‖≦‖S‖・‖T‖
となる。また、T*∈Mである。
このMを全作用素環といい、その部分環でノルム位相で閉じているものをC*環、弱位相で閉じているものをノイマン環という。その研究はノイマンに始まり、量子力学などへの応用もあって、第二次世界大戦後急速な発展を遂げた部門である。
有界線形作用素でA*=Aとなるものを自己共役作用素という。これがさらに完全連続ならば、対称行列と同様なスペクトルの定理が成り立つ。すなわち、
Ax=λx, x≠0
となるxが存在するとき、λをAの固有値、xを固有値λに対する固有ベクトルということにすると、次のことが成り立つ。「自己共役、完全連続な作用素Aに対し、固有値の列{λn}:|λ1|≧|λ2|≧……→0と、対応する固有ベクトルの列{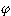 n}が選べて、{
n}が選べて、{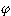 n}は正規直交系(〈
n}は正規直交系(〈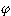 i,
i,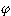 j〉=1,〈
j〉=1,〈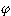 i,
i,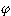 j〉=0,i≠j)となり、
j〉=0,i≠j)となり、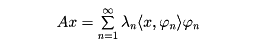
の形に展開できる」
[洲之内治男]
改訂新版 世界大百科事典 「ヒルベルト空間」の意味・わかりやすい解説
ヒルベルト空間 (ヒルベルトくうかん)
Hilbert space
ユークリッド空間の概念を無限次元に拡張した空間。積分方程式の問題に関連してD.ヒルベルトにより導入され,J.フォン・ノイマンによって公理化された。複素ユークリッド空間の二つのベクトルx,yの内積(x,y)は次の性質をもつ。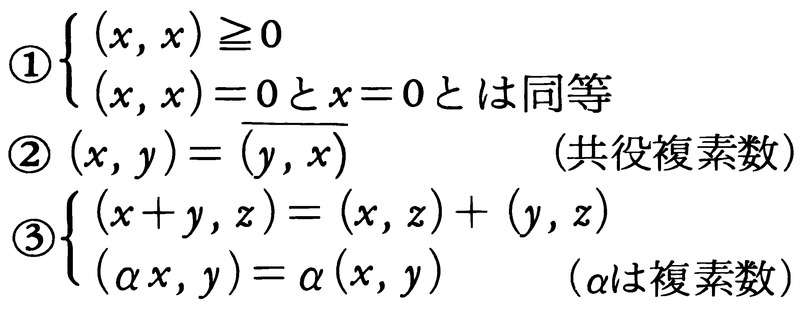
ベクトルxの長さを/x/と書くと, であって,シュワルツの不等式,
であって,シュワルツの不等式,
(5)|(x,y)|≦/x/・/y/
が成立する。一般に,複素数体上のベクトル空間(有限次元とは限らない)Xがあって,任意のx,y∈Xに対してその内積と呼ばれる量(x,y)が定義されて(1),(2),(3)を満たすとき,Xを内積空間という。内積空間において(4)で定義される/x/をxのノルムという。この場合にも有限次元の場合と同様に(5)が成立する。さらにdis(x,y)=/x-y/は距離の性質をもち,Xは距離空間になる。内積空間は,その内積から上のように定義されたノルムによる距離に関して完備なとき( となるxが存在するとき),ヒルベルト空間と呼ばれる。ヒルベルト空間はバナッハ空間でもある。
となるxが存在するとき),ヒルベルト空間と呼ばれる。ヒルベルト空間はバナッハ空間でもある。
ヒルベルト空間の例を二つあげる。
(1)実数の区間(a,b)上の複素数値可測関数x(t)で|x(t)|2が積分可能なものの全体をL2(a,b)とし,内積を, と定義する。
と定義する。
 なる複素数列{ξi}の全体をl2とし,x={ξi},y={ηi}∈l2の内積を,
なる複素数列{ξi}の全体をl2とし,x={ξi},y={ηi}∈l2の内積を, と定義する。L2(a,b),l2はいずれもヒルベルト空間である。
と定義する。L2(a,b),l2はいずれもヒルベルト空間である。
ヒルベルト空間Xの二つの元x,y∈Xは(x,y)=0なるとき直交するという。例えばL2(0,2π)において{sinnx,cosnx;n=0,1,2,……}のどの二つも互いに直交する。
ヒルベルト空間を扱う現代解析学の考え方については,〈関数解析学〉の項目を参照。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「ヒルベルト空間」の意味・わかりやすい解説
ヒルベルト空間
ヒルベルトくうかん
Hilbert space
(1) H の二つの元 f と g に対して,f+g と af(a は複素数)が定義され,これらの演算に関して H は複素数上のベクトル空間である。
(2) H の二つの元 f と g に対して,それらの内積と呼ばれる複素数(f,g)が対応し,次の性質をもつ。
(a) (f+f',g)=(f,g)+(f',g)
(b) (af,g)=a(f,g)
(c)
 (ただし
(ただし  は(f,g)の共役複素数)
は(f,g)の共役複素数)(d) (f,f)≧0 で,(f,f)=0 となるのは f=0 のとき,そしてそのときにかぎる。
(3) ∥f∥=(f,f)1/2 とおき,f と g の距離をρ(f,g)=∥f-g∥で定義すれば,H は完備な距離空間である。
(4) H の次元は有限ではない。
(5) H は可分である。
(4) は無限次元で,(5)はそれが可算ということであるが,今日では一般次元で考えるために,(4)と (5)は仮定しないことが多い。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「ヒルベルト空間」の意味・わかりやすい解説
ヒルベルト空間【ヒルベルトくうかん】
→関連項目空間(数学)
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内のヒルベルト空間の言及
【関数解析学】より
…このようにベクトル算法と収束概念の定義された空間の構造や,その空間における作用素の性質を一般的に調べることにより,従来は別個のものと考えられてそれぞれの方法で取り扱われていたいくつかの理論が,統一された簡単な方法で,より一般的に扱われるようになり,また他方において,多くの新しい事実を導くことができるようになった。こうして現代化された解析学の基礎となる部門が関数解析であり,その理論の代表として,20世紀前期に創始されたヒルベルト空間論,バナッハ空間論,20世紀中期に創始された超関数論があげられる。このうち,バナッハ空間論とヒルベルト空間論の概略について以下に述べるが,〈バナッハ空間〉〈ヒルベルト空間〉の定義や例は,それぞれの項目を参照されたい。…
※「ヒルベルト空間」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
1 食肉目クマ科の哺乳類の総称。全般に大形で、がっしりした体格をし、足の裏をかかとまで地面につけて歩く。ヨーロッパ・アジア・北アメリカおよび南アメリカ北部に分布し、ホッキョクグマ・マレーグマなど7種が...

