日本大百科全書(ニッポニカ) 「三平方の定理」の意味・わかりやすい解説
三平方の定理
さんへいほうのていり
直角三角形ABCが与えられたとき、斜辺BCを1辺とする正方形の面積は、他の2辺AB、ACを1辺とする二つの正方形の面積の和に等しい。すなわち、
BC2=AB2+AC2
が成立する。これを三平方の定理という。紀元前540年ごろギリシアの数学者ピタゴラスが発見したものといわれ、ピタゴラスの定理として知られている。日本では三平方の定理という呼び方が第二次世界大戦中に考案され、以後通称となった。この定理の逆も成り立つ。すなわち、三角形の1辺の平方が他の2辺の平方の和に等しければ、始めの辺に対する頂角は直角である。この逆定理の成立によって、たとえば、辺の長さが3、4、5である三角形は32+42=52であるから、直角三角形となる。この3、4、5の関係を用いて直角をつくる方法は、古代エジプトや古代中国においても土地の区画などに用いられたという。和算(江戸時代の数学)においても、三平方の定理は勾股弦(こうこげん)という呼び名で知られていた。弦とは直角三角形の斜辺のことで、勾と股は残りの2辺の短いほうと長いほうのことを表している。
等辺を1とする直角二等辺三角形の斜辺の長さが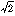 になることは、無理数というまだ知られていなかった数の発見のきっかけとなった。一方、3、4、5のような三平方の関係を満足する整数の組をピタゴラス数という。mとnを正の整数とすると(m>n)、
になることは、無理数というまだ知られていなかった数の発見のきっかけとなった。一方、3、4、5のような三平方の関係を満足する整数の組をピタゴラス数という。mとnを正の整数とすると(m>n)、
m2-n2, 2mn, m2+n2
はピタゴラス数になる。三平方の定理は平面や空間の2点間の距離の公式の基礎でもある。
[柴田敏男]
『大矢真一著『ピタゴラスの定理』(1975・東海大学出版会)』
改訂新版 世界大百科事典 「三平方の定理」の意味・わかりやすい解説
三平方の定理 (さんへいほうのていり)
∠Aが直角である△ABCの3辺BC,CA,ABの長さをa,b,cとするとき,a2=b2+c2という関係が成り立つ(図1)。すなわち,直角三角形ABCの斜辺BCを1辺とする正方形の面積は,辺CAを1辺とする正方形の面積と辺AB上に作った正方形の面積の和に等しい(図1)。これはユークリッド幾何学におけるもっとも重要な定理の一つで,三平方の定理と呼ばれている。この定理は古代ギリシアの哲学者ピタゴラスによって発見されたといわれ,ピタゴラスの定理とも呼ばれているが真偽のほどは定かでない。三平方の定理の逆も成り立つ。すなわち,△ABCの3辺BC,CA,ABの長さa,b,cの間にa2=b2+c2という関係が成り立てば,∠Aは直角である。この特別の場合として,3辺の長さの比が3:4:5である三角形は直角三角形となるが,この事実は古くからエジプト,バビロニア,インドなどで知られ,直角を作るのに利用された。三平方の定理は次のように拡張される。直角三角形の3辺の上に相似形をこれらの3辺が対応するように作れば,斜辺の上の図形の面積は直角をはさむ2辺の上の図形の面積の和に等しい(図2)。西洋でも東洋でも古くから三平方の定理のいろいろの証明法が考案された。代表的な方法を三つ(図3,4,5)あげておいたが,図3に示したものはもっとも有名なもので,ユークリッドの《ストイケイア》に書かれている図形的に証明する方法である。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「三平方の定理」の意味・わかりやすい解説
三平方の定理【さんへいほうのていり】
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「三平方の定理」の意味・わかりやすい解説
三平方の定理
さんへいほうのていり
「ピタゴラスの定理」のページをご覧ください。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
関連語をあわせて調べる
ローマ法王ともいう。ラテン語 Papaの称号はカトリック教会首長としてのローマ司教 (教皇) 以外の司教らにも適用されていたが,1073年以後教皇専用となった。使徒ペテロの後継者としてキリスト自身の定...





