円周率（読み）エンシュウリツ

デジタル大辞泉

えんしゅう‐りつ〔ヱンシウ‐〕【円周率】

円周の、直径に対する比。記号はπパイで表し、値は3.14159…で、ふつう3.14として計算する。

出典　小学館

精選版 日本国語大辞典

えんしゅう‐りつヱンシウ‥【円周率】

1. 〘 名詞 〙 円周の、直径に対する比率。π(パイ)であらわす。値は、三・一四一五九二…。〔暦象新書（1798‐1802）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

円周率 (えんしゅうりつ)

どのような円をとっても，円周の長さの直径に対する比は一定である。この比の値を円周率といい，周を意味するギリシア語perimetrosの頭文字をとってπで表す。西欧語には円周率に相応する術語はなく，それは単に数πとか，あるいはアルキメデスの数と呼ばれている（ドイツではしばしばπをルドルフの数と呼ぶ）。

　πは無理数で，その第50位までの小数は3.14159265358979323846264338327950288419716939937510であるが，実用的計算では3.14，少し精密な計算でも3.1416でまにあう。πの近似値としては3が古くから用いられ，古代エジプトでは（4/3）⁴も用いられていた。アルキメデスは円に内接および外接する正96角形の周を計算してを示し，πの小数点以下第2位までの正確な値を理論的に導いた。5世紀ころには，πの近似値としてインドのアールヤバタĀryabhaṭaは3.1416を，中国の祖沖之はやを得ている。16世紀には，ルドルフS.von Rudorff（1540-1610）はπの近似値を小数点以下第35位まで計算し，フランスのF.ビエトは図に示すような公式を得た17世紀に入って微積分が発見されてからは，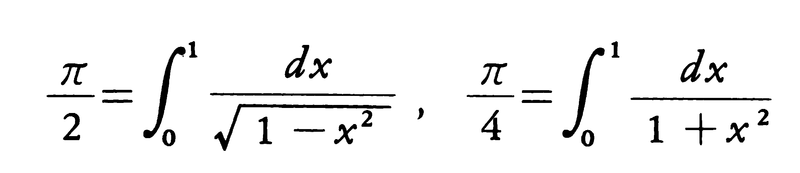

のようなπを定積分に結びつける式が得られ，これらを用いて，πを無限級数の和，あるいは種々の形の極限値として表示する式が得られ，πの近似値も精密に計算できるようになった。例えば無限級数で表す公式に，

があり，無限積に表す公式に，がある。さらに，連分数で表すものに，

がある。πの近似値としては1873年にシャンクスW.Shanksが小数点以下第707位まで算出したのがながく記録とされていたが，その値の小数点以下第528位に誤りがあることが1946年に発見された。17～18世紀の和算家たちもπの値を第50位まで計算していた。現在では電子計算機の発達により100万桁以上でも容易に求められるようになった。πが無理数であることは1761年ランバートJ.H.Lambertにより証明されたが，さらに，1882年リンデマンC.L.F.Lindemannはπが超越数，すなわち整数を係数とする代数方程式の根とならない数であることを証明した。
執筆者：中岡 稔

コラム－円周率の覚え方

図－ビエトの公式

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

円周率
えんしゅうりつ

円の直径の長さに対する円周の長さの比は一定で、この比の値を円周率という。円周率をギリシア文字π(パイ)で表す。πの値は大型コンピュータにより小数点以下数千億桁(けた)以上も計算されており、2002年（平成14）には1兆2411億桁が記録されている（東京大学情報基盤センター、日立製作所）。半径rの円の周の長さは2πr、面積はπr²である。πの近似値を小数点以下14桁まで示すと、3.14159265358979である。これを覚えるのに「身一つ世人行くに無意味違約なく」「産医師異国に向かう。産後やくなく」など、いろいろな語呂(ごろ)合せが知られている。紀元前1550年ころエジプトの数学書として有名なアーメスのパピルスには、半径1の円の面積、すなわち、円周率の近似値として3.1605が記録されている。ギリシアの時代には有名な三つの作図問題の一つとして、円と等面積の正方形の作図が研究された。そのころ「円の面積は直径の2乗に比例する」ことが知られており、その比例定数はπ／4であるから、円周率というより円積率として考えられたのが始まりであろう。アルキメデスは円に内接および外接する正九十六角形の面積を求め、円周率の値が3.140と3.142の間にあることを示した。円周率の近似値として22／7すなわち3.1428……がアルキメデスをはじめ古代インド、中国でも用いられた。円周率を表す記号πはオイラーが1737年に採用して以来一般に使用されている。微積分の発展以降πの値を表す級数がいろいろと示されている。πが超越数（整係数あるいは有理数係数の代数方程式の根(こん)とならない数）であることはリンデマンC. L. F. Lindemannが1882年に証明し、円と等積な正方形を定規(じょうぎ)とコンパスで作図することは不可能であることが示された。

［柴田敏男］

『村田全著『日本の数学　西洋の数学』（中公新書）』

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

円周率
えんしゅうりつ
pi

平面上の円の円周と直径との比の値。すべての円で等しい。3.14のほか 22/7という数値がよく用いられる。小数点以下 31桁までの値は，3.1415926535897932384626433832795。この値を示すのに記号π（パイ）を用いるようになったのはレオンハルト・オイラーの著作による。πは無理数であり，超越数である。前2000年頃のバビロニア人（→バビロニア）は，円に内接する六角形から 3.125という円周率を算出しており，古代エジプト人は約 3.16045という数値を用いていたことが前1650年頃のパピルスから明らかになっている。アルキメデスは円に内接および外接する正多角形（→多角形）から，円周率は 223/71より大きく，22/7より小さいことを導き出した。今日ではスーパーコンピュータを使って計算されるが，2010年にフランスで通常のコンピュータを使用して計算した約 2兆7000億桁の数値が発表された。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

円周率【えんしゅうりつ】

円周の長さを直径で割った比の値で無理数。記号π。3.141592653589……で，3.14，22/7，333/106，355/113等を近似値に用いる。πの近似値としては1873年にW.シャンクスが小数点以下第707位まで算出したが，その第528位に誤りがあることが1946年に発見された。現在ではコンピューターの発達により，πの近似値は10兆桁以上でも求められるようになった。2013年12月現在小数点以下12.1兆桁という報告がある。→円／円理／円積問題
→関連項目アールヤバタ｜近似値｜祖沖之｜超越数

出典　株式会社平凡社

知恵蔵

円周率

円の周囲の長さと直径の比として与えられる数。3.14……。紀元前2000年のバビロニア、古代エジプトでは少数点以下1位まで、紀元前1200年の中国では整数部分の3が正しく計算されていた。また、紀元前250年、アルキメデスは3.14までの正確な値を得ていた。2005年末現在のπの値計算の世界記録は、東京大学情報基盤センターの金田康正教授のグループが得た1兆2411億桁。

(桂利行 東京大学大学院教授 ／ 2007年)

出典　(株)朝日新聞出版発行「知恵蔵」

世界大百科事典（旧版）内の円周率の言及

【アルキメデス】より

…それが《球と円柱について》や《円錐状体(回転放物線体，回転双曲線体)と球状体(回転楕円体)について》など多くの著作であるが，それらを現在われわれは，ハイベルクJ.L.Heibergの編纂したギリシア語テキスト(《アルキメデス全集》3巻，1910‐15)で読むことができる。またアルキメデスの学問の性格を知る上で忘れてはならないのが，有名な円周率の数値による近似計算であろう。ユークリッド《ストイケイア》では，〈円は互いに直径上の正方形に比例する〉と書かれているのみであって，円の面積や円周率にはいっさいふれられていない。…

【遺題継承】より

…なかには，前者の解答だけを示して出版された数学書もあり，また，数学の解説書から離れて，前者の解答と自己の出題だけの数学書も刊行されるようになった。遺題継承の間に従来不統一であった円周率の値が問題となった。すなわち，3.16と3.162その他である。…

【円】より

…このため古くから円の大きさは半径よりもむしろ直径と結びつけて考えられ，円周の長さの直径の長さに対する比が考察された。この比の値は円の大きさによらない一定の数で，円周率と呼ばれ，ふつうπという文字で表される。πは無理数で，実用的な計算ではその近似値3.14または3.1416が用いられる。…

【祖沖之】より

…南朝の宋の時代(420‐479)に歳差の効果を考慮して新暦を作ったが，この暦法は息子の祖（そけん）の努力によって梁の時代に大明暦として官暦に採用された(510)。また円周率の値を335/113(密率)と決め，近似値を22/7(約率)とした。指南車，千里船，水碓磨などの機械を設計した技術者でもあり，また斉(479‐502)のときには〈安辺論〉を書いて屯田，農殖を勧めた。…

【中国数学】より

…また約分についてはユークリッドの方法が述べられている。3世紀半ばの魏の劉徽はこの書に対しすぐれた注釈を書いたが，その中で円周率の計算を論じ，近似値として3.1416を得ている。漢･唐の間の数学書としては《九章算術》を含む〈十部算経〉《算経十書》があるが，この中の《綴術》を書いた劉宋(420‐479)の祖沖之は円周率を研究し，密率として355/113，約率として22/7を求めた。…

【張衡】より

…候風地動儀とよばれた世界最古の地震計の製作のほかに記里鼓車(里程計)あるいは指南車の設計者としても知られている。彼は数学者としても優れ，円周率の値として，3.16＜π＜3.18を算出した。【橋本 敬造】。…

【劉徽】より

…《重差》は唐代に《海島算経》と称された。《九章算術》の注には多くの創見が見られるが，割円術によって円周率を求める算法には極限の考えが用いられ，円に内接する正192角形の面積によってπ＝3.14という近似値を決定し，正3072角形の面積によって3.1416を求めた。【橋本 敬造】。…

※「円周率」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」