平行線公理（読み）へいこうせんこうり

日本大百科全書(ニッポニカ)

平行線公理
へいこうせんこうり

平面上の二直線が交点をもつかどうかを規定する公理をいう。次の三通りの平行線公理が考えられる。（P）平面上で直線外の1点を通って、この直線と交わらない直線がただ1本存在する。（H）平面上で直線外の1点を通って、この直線と交わらない直線が少なくとも2本存在する。（E）平面上の二直線はかならず交わる。公理（P）がユークリッド幾何学を、公理（H）が双曲幾何学を、また、公理（E）が楕円(だえん)幾何学（球面幾何学）を規定する。

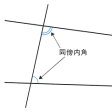
　ユークリッドの『幾何学原本』Stoikheiaにおける第五公準「二直線に第三の直線が交わり、その一方の側にできる二つの角（いわゆる同傍内角、図参照）の和が二直角より小さいときは、その二直線はその側において交わる」は、他の公準の下では平行線の一意性と同等である。また、ヒルベルトの公理系は結合、順序、合同、平行線、連続性の五群からなるが、そのなかの平行線公理は平行線の一意性を保証している。ユークリッドの『幾何学原本』の場合も、ヒルベルトの公理系の場合も、平行線の存在は他の公理から証明される。歴史的には、ユークリッドの第五公準の独立性に疑問がもたれたことによっていわゆる非ユークリッド幾何学が誕生した。

［荻上紘一］

[参照項目] | 幾何学基礎論 | 非ユークリッド幾何学

同傍内角〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

平行線公理【へいこうせんこうり】

ユークリッドの《幾何学原本》にある５番目の公準をいう。これは〈一直線外の一点を通ってこの直線に平行な直線は一つあり，ただ一つに限る〉と同値。他の公準より形が複雑なため，他の公理・公準から証明する試みが繰り返されたがすべて失敗。これを他の公理でおきかえても矛盾のない非ユークリッド幾何学が成立することから，独立の公理であることが証明された。
→関連項目公理｜ユークリッド幾何学

出典　株式会社平凡社