精選版 日本国語大辞典 「微分方程式」の意味・読み・例文・類語
びぶん‐ほうていしき‥ハウテイシキ【微分方程式】
- 〘 名詞 〙 数学で、未知関数の導関数を含む方程式のこと。未知関数が一変数のとき常微分方程式、多変数のとき偏微分方程式と呼ばれる。〔工学字彙(1886)〕
改訂新版 世界大百科事典 「微分方程式」の意味・わかりやすい解説
微分方程式 (びぶんほうていしき)
differential equation
独立変数とその関数およびそれの導関数を含む方程式を微分方程式,その方程式を満足させる関数をその解と呼ぶ。微分方程式にあらわれる未知関数が1変数の関数であるとき,それを常微分方程式,多変数の関数であるとき偏微分方程式という。ここでは常微分方程式に話を限る。
tを独立変数,x1,……,xnをtの未知関数とするとき,微分方程式,
を正規形,あるいは標準形の微分方程式という。多くの常微分方程式がこの形に帰着される。例えばxを未知関数とする微分方程式,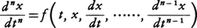
は,x=x1,dx/dt=x2,……,dn⁻1x/dtn⁻1=xnとおくことにより,正規形の方程式,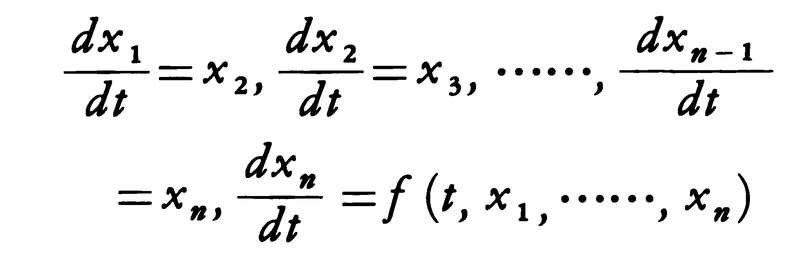
に直すことができる。したがって常微分方程式に関する定理の多くは正規形の方程式に対して述べられている。
正規形の方程式(1)において,条件,
t=t0においてx1=x10,x2=x20,……,xn=xn0 ……(2)
を満たす解を求める問題を初期値問題,(2)を初期条件という。
f1,……,fnが(t,x1,……,xn)を座標とするn+1次元空間内の開集合Gにおいて定義され,そこで連続なときには,任意の(t0,x10,……,xn0)∈Gに対し(2)を満たす解x1=x1(t),x2=x2(t),……,xn=xn(t)はつねに存在する。さらにf1,……,fnがGにおいて局所リプシッツ条件,すなわち〈KをG内の任意の有界閉集合とするとき,定数Lk>0が存在して(t,x1,……,xn)∈K,(t,x1′,……,xn′)∈Kならば,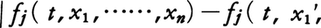
 が成り立つ〉ならばそのような解はただ一つに限る。解は開区間(α,ω)で定義されるが,その定義域は一般に初期条件に依存する。
が成り立つ〉ならばそのような解はただ一つに限る。解は開区間(α,ω)で定義されるが,その定義域は一般に初期条件に依存する。
f1,……,fnがx1,……,xnの一次式であるとき,すなわち微分方程式が,
のような形であるとき,それを線形微分方程式という。ajk(t),bj(t)がすべてある開区間Iで連続とし,t0∈Iとすれば任意のx10,……,xn0に対し初期条件(2)を満たす解はただ一つ存在し,それはつねにI全体で定義される。
x1,……,xnおよびb1(t),……,bn(t)を成分とするn次元列ベクトルをそれぞれx,b(t)と書き,ajk(t)を要素とするn次正方行列をA(t)と書けば,(3)は,
と書かれる。b(t)≡0のとき(4)(したがって(3))は斉次,そうでないときは非斉次とよばれる。斉次方程式,
はつねに一次独立なn組の解をもち,任意の解はそれの線形結合となる。したがって一次独立なn組の解を列とする行列をΦ(t)で表せば,(5)の一般解はx=Φ(t)c(cは定数ベクトル),t=t0でx=x0となる解はx=Φ(t)Φ⁻1(t0)x0と表される。Φ(t)を(5)の基本行列,解の基本系,基本解などとよぶ。(5)の基本解Φ(t)がわかれば,(4)のt=t0でx=x0となる解は,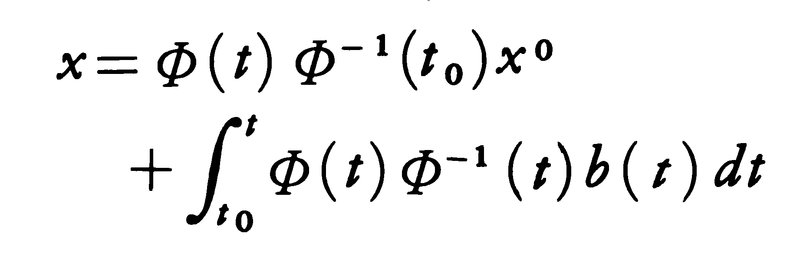
となることがわかっている。(5)の基本解を求める一般的方法は知られていないが,A(t)がとくに定数行列Aであるときはetaが(5)の基本解になる。ただしetaは行列の無限級数,
によって定義される行列である。Aが与えられたときこの無限級数の和を具体的に計算する方法もわかっている。線形方程式についてはこのほかにもいろいろな結果が得られている。また境界値問題についても多くのことが知られている。
非線形方程式の研究は線形の場合に比べて多くの困難を伴う。正規形の非線形方程式(1)の解が一つ求められたとし,それをxj=φj(t)(j=1,……,n)とするとき,この解の近傍にある他の解を調べるには,ふつう変数変換xj=φj(t)+yjを行って(1)を,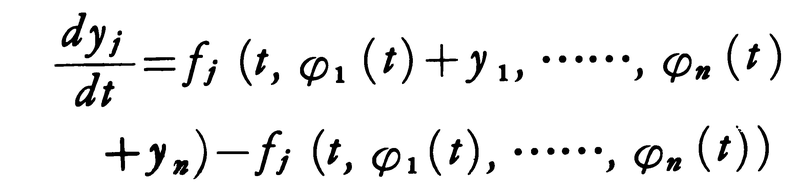
と変形する。この右辺のテーラー展開の第1項のみをとって得られる線形方程式,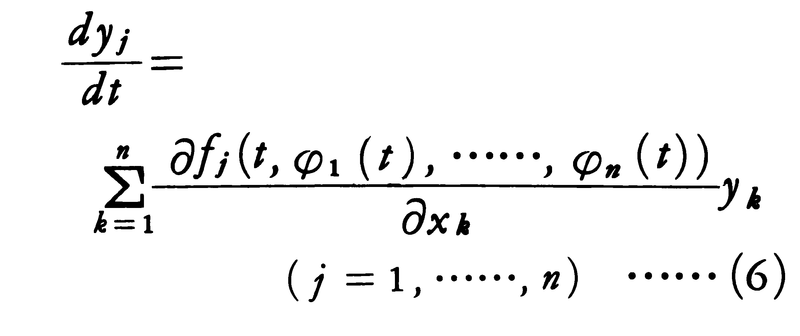
を(1)の変分方程式variational equationとよぶ。(6)の解の性質を利用して(1)の解の性質を調べるのがいわゆる線形化の方法で,一つの解の近傍の状況を調べる局所的研究の大部分はこの線形化の方法に依存している。その典型的なものの一つとして解の安定性の研究がある。
非線形方程式の解の大域的研究は非常に困難であるが,(1)の右辺がtを陽に含まない場合,いわゆる自律系(自励系)autonomous systemの場合には位相的方法がかなり有効である。H.ポアンカレはn=2の場合に対してこのことを示した。現在,ポアンカレ=ベンディクソンの理論とよばれているのがそれである。この位相的研究はその後多くの学者によって続けられ力学系の理論へと発展した。
t,x1,……,xnを複素変数とみなしたとき,(1)の右辺が複素解析的である場合には解xj(t)を複素変数tの複素解析関数とみなす立場で微分方程式を取り扱うことができる。このとき,各fj(t,x1,……,xn)がt=t0,xj=xj0(j=1,……,n)において正則ならば,初期条件(2)を満たす解はただ一つ存在してt=t0において正則である。したがってt=t0の近傍でt-t0の収束べき級数によって表される。これを複素t平面上で可能な限り解析接続することによって大域的解が得られるが,fjがすべて1価解析関数であっても,解は一般に多価関数であって,しかもそれの分岐点の位置は初期値に依存するのがふつうである。このように初期値に依存する解の分岐点を動く分岐点という。ただし方程式が線形,すなわち(3)のような形であるときには,解の分岐点は係数の特異点にのみあらわれ,したがって動く分岐点は存在しない。複素領域における斉次線形微分方程式,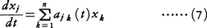
あるいは,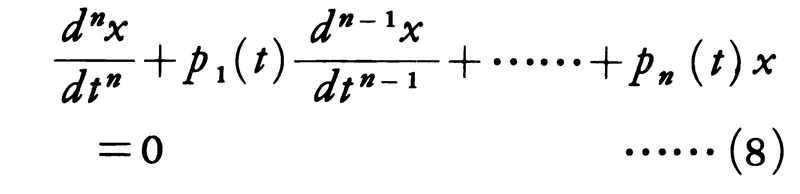
の理論はG.F.B.リーマンおよびフックスL.Fuchs(1833-1902)によって展開された。それの重要な部分はajk(t),あるいはpk(t)がt=t0において極をもつ場合に,解がそこでどのような特異性を示すかについての研究であって,例えば(8)の場合には,微分方程式のn個の一次独立な解として, (j=1,……,n)のような形のものをとることができる。ここにλjは複素定数で,φj(t)は領域0<|t-t0|<r(rはある正の数)で1価正則な関数である(例外的にはlog(t-t0)を含む項があらわれることもある)。φj(t)がt0でたかだか極しかもたないときt0を(8)の確定特異点,t0に真性特異点をもつときt0を(8)の不確定特異点という。t0が確定特異点のときには定数λjおよびφj(t)のt0におけるローラン展開の係数をすべて計算できる。
(j=1,……,n)のような形のものをとることができる。ここにλjは複素定数で,φj(t)は領域0<|t-t0|<r(rはある正の数)で1価正則な関数である(例外的にはlog(t-t0)を含む項があらわれることもある)。φj(t)がt0でたかだか極しかもたないときt0を(8)の確定特異点,t0に真性特異点をもつときt0を(8)の不確定特異点という。t0が確定特異点のときには定数λjおよびφj(t)のt0におけるローラン展開の係数をすべて計算できる。
特異点がすべて確定特異点であるような線形微分方程式をフックス型微分方程式とよぶ。
2階のフックス型微分方程式,
においては,特異点の数が2以下のものはすべて求積法で解くことができる。特異点の数が3の場合,その解全体のつくる関数族はリーマンのP関数とよばれ,その性質が非常にくわしく調べられている。なおこの場合には,適当な変数変換を行うことによって,(9)をガウスの微分方程式,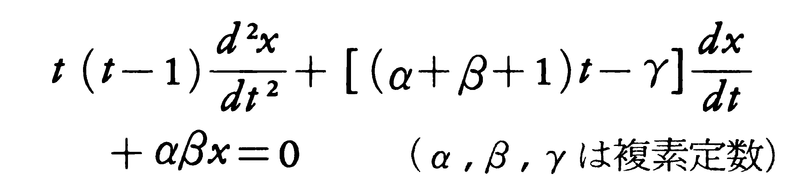
に変換することができる。したがって3個の特異点をもつ2階フックス型微分方程式の研究はガウスの微分方程式の研究に帰着される。
t0が不確定特異点である場合には,λjやφj(t)を具体的に計算することはできない。しかしこの場合には,これとはまったく異なった形の形式解が存在することがトメR.W.Thoméによって示された。この形式解は実際に計算可能である。ただしその中にあらわれるべき級数はたいていの場合発散してしまうので,そのままではこの形式解は意味をもたないが,ポアンカレは解析関数の漸近展開という概念を導入することにより,この形式解に解析的意味付けをすることに成功した。
非線形微分方程式においては,すでに述べたように動く分岐点があらわれるので解の性質の研究はきわめてむずかしくなる。これについてパンルベPaul Painlevé(1863-1933)は,(1)1階微分方程式の動く分岐点はすべて代数分岐点である,(2)動く分岐点をもたない1階微分方程式はすべてリッカティ型の微分方程式に帰着できる,という二つの重要な結果を証明した。さらに彼は2階の微分方程式が動く分岐点をもたない条件を研究し,そのようなものは本質的に6個の標準形に帰着できることを示した。しかし3階以上の方程式に対してはこのような有力な結果は得られていない。
非線形方程式の解は,その動かない特異点,すなわちすべての解に共通な(したがって初期条件に依存しない)特異点においては,一般に複雑な特異性を示す。これについては,ブリオC.A.A.BriotおよびブーケJ.C.Bouquetをはじめとして,多くの学者たちの研究があり,動かない特異点の近傍における解の展開式についてかなり豊富な成果が得られている。
常微分方程式の理論は1階偏微分方程式とも密接な関係がある。また,制御関数を含む微分方程式についての,いわゆる制御系の理論や,解の挙動が初期条件のみならず,解の過去の挙動に依存する微分差分方程式や積分微分方程式などの関数微分方程式,あるいは微分方程式が確率空間上のパラメーターを含む確率微分方程式など,近年になって登場したいろいろな関数方程式の研究において,常微分方程式の理論はその基本的なモデルとして重要な役割を果たしている。
→境界条件 →初期条件
執筆者:斎藤 利弥
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「微分方程式」の意味・わかりやすい解説
微分方程式
びぶんほうていしき
differential equation
変数xと、その関数yとの関係を、x、yやその導関数を含む方程式の形で表したものを微分方程式という。微分方程式は、独立変数が一つの常微分方程式と、独立変数が2個以上で偏導関数を含む偏微分方程式とに分けられる。ここでは、微分方程式の理論の歴史的形成について述べる。
ガリレオが落体の運動を研究していて、時間tの間に落下する距離をx(t)とすると、加速度
x″(t)=g(一定)
であることを発見し、その解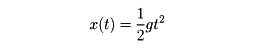
を得たのが、微分方程式が解かれた最初であるといわれている。これはニュートンやライプニッツの微分積分の始まる50年も前(1680ころ)である。微分方程式が本格的に研究されるのはニュートン以後で、まず18世紀前半は、特殊な方程式をそれ特有の方法で解いていた(求積法)が、後半には級数による解法が用いられるようになる。1820年ごろコーシーが、微分方程式の解の存在を調べる必要があることを強調して、理論的な研究が始まり、さらに、ポアンカレの漸近級数による解法などから、常微分方程式の解の定性的な研究が始まった。
偏微分方程式は18世紀の中ごろまでは現れない。ダランベールが、x軸上の区間[0,1]に張られた弦の振動の方程式は、時間t、場所xにおける変位をu(t,x)とすると、
で表されることを示し、その解は
u(t,x)=f(x-ct)+g(x+ct)
(f,gは任意の関数)
となることを示している。さらに、ベルヌーイなどにより、ポテンシャルの方程式や熱伝導の方程式などが導入され、フーリエになって、フーリエ級数による解法が応用上成功し、フーリエ級数論の発端となった。
[洲之内治男]
物理現象と微分方程式
ほとんどすべての物理法則は、これを微分方程式の形に表現することができる。たとえば、運動の法則は、質点の座標の時間に関する二階微分方程式として表され、電磁場に関する法則は、電場と磁場の時間と空間に関する一階の連立偏微分方程式、すなわちマクスウェル方程式の形をとっている。これらの法則に基づいて物理現象を量的に理解するためには、法則を数学的に表現した微分方程式を解かなければならない。
微分方程式の一般解は任意定数または任意関数を含んでいる。これらの任意定数または任意関数を決定するには、対象とする物理現象の物理的条件を用いればよい。ニュートンの運動の法則は、力の作用のもとで速度がどのように変化するかを与えているにすぎないため、運動法則に対応する微分方程式の解には、速度の変化が同じであっても位置や速度のさまざまな運動に対応するものが含まれている。この解の多様性が一般解の2個の積分定数である。したがって微分方程式の解は、任意の時刻の質点の位置や速度を物理条件として与えることによって初めて一義的に定まる。
偏微分方程式の一般解に含まれている任意関数は、ある特定の領域における解の値を与えることによって定まる場合が多い。このような条件を与えられて解かれる微分方程式を境界値問題という。この場合、物理的条件は特定領域の関数値すなわち境界値によって与えられる。
[田中 一]
ブリタニカ国際大百科事典 小項目事典 「微分方程式」の意味・わかりやすい解説
微分方程式
びぶんほうていしき
differential equation
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「微分方程式」の意味・わかりやすい解説
微分方程式【びぶんほうていしき】
→関連項目解析学|カルタン|求積法|コーシー|差分法|三体問題|ピカール|微分解析機|方程式|ラプラス|リウビル
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の微分方程式の言及
【数値解析】より
…数値計算法とか実用解析などの名まえでも呼ばれており,行列の計算や微分方程式の解法など広く科学の諸分野に現れる問題を数値的に取り扱うことを目標とする。そこでは数学における古典解析学が主要な手段を提供しているが,最近は各種の計算機を用いた機械計算の飛躍的発展に伴い,それに応じた種々の技法が開発されている。…
【微積分学】より
…微積分の数学的な内容については,〈微分〉〈積分〉などの項目を参照されたい。未知関数の導関数を含む方程式を微分方程式というが,微分方程式を解くことは微積分の直接の応用であって,現在では微積分学という名称の中に微分方程式の初等的理論や解き方を含めることもある。自然現象や自然の法則は微分方程式で記述されるものがきわめて多い。…
※「微分方程式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
目次 飼養文化 北アメリカ 北方ユーラシア偶蹄目シカ科の哺乳類。北アメリカでは野生種はカリブーcaribouと呼ばれる。角が雄だけでなく雌にもふつうある。体長130~220cm,尾長7~20cm,...

