振動（読み）シンドウ（その他表記）oscillation
vibration

デジタル大辞泉

しん‐どう【振動】

［名］(スル)
１ 揺れ動くこと。「爆音でガラス戸が振動する」
２ ある量が、一つの状態を中心に周期的に変動すること。振り子・ばねの運動や電気振動など。
３ 数学で、無限に続く数列・関数列の極限が不定で、収束せず、また極限値が無限大でもないこと。
[類語]震動・動揺・激動・震撼・動く・振れる・揺れる・揺らぐ・上下する・微動する・ぐらつく・動かす・揺らす・揺する・揺さぶる・揺すぶる・揺り動かす・揺り返す・揺る・揺るがす・揺れ・縦揺れ・横揺れ

出典　小学館

精選版 日本国語大辞典

しん‐どう【振動】

1. 〘 名詞 〙
2. ① ゆれ動くこと。動揺すること。また、ゆり動かすこと。
   1. [初出の実例]「敏達天皇のみ代、和泉の国の海中に楽器の音声あり、笛箏琴箜篌(くご)等の声の如く、或るは雷の振動するが如し」(出典：日本霊異記（810‐824）上)
   2. [その他の文献]〔春秋左伝‐襄公四年〕
3. ② ほぼ一定の周期をもって繰り返される運動。単振動、周期的振動など。
   1. [初出の実例]「是れ擺の振動(シンドウ)（〈注〉フリ）を助け、其快慢の度を節する者にして」(出典：造化妙々奇談（1879‐80）〈宮崎柳条〉八)
4. ③ 電磁場や電流の強さなどが、ある波形で繰り返しの時間的変化をすること。
5. ④ ＝ひょうどう（秤動）
   1. [初出の実例]「太陰は、其一周天の間に一自転をなして、其一方常に地球に向ふと雖ども、微く東西に転ずることあり。これを振動と云ふ」(出典：遠西観象図説（1823）中)
6. ⑤ 数学で、数列や関数が上下に変動し、極限がなく、無限大にもならないこと。
7. ⑥ 中国古代の礼拝法。周代の九拝の一つ。手の平を打ち合わせるもの。かしわで。振動拝。
   1. [初出の実例]「日本に周礼にまのあたり残りたるは、九拝の中の振動ぞかし、珍らしき事也」(出典：随筆・文会雑記（1782）附録)
   2. [その他の文献]〔周礼‐春官・太祝〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

振動 (しんどう)
oscillation
vibration

糸の一端におもりを結びつけ，他の端を支えて振子を作り，静かにつるすと，おもりは支点の鉛直下方に静止する。この状態でおもりを水平方向に軽くはじくと，おもりは支点を中心として糸の長さを半径とする鉛直面内の円周に沿って，その最下点の付近で往復運動を繰り返す。この運動が振動の典型的な例である。このような振動は日常われわれの身の回りで数多く見ることができる。例えば天井からつり下げた電灯，電車のつり皮，クレーンの腕の先端からつり下げられた滑車などが揺れ動くのはすべて振動である。振動にはこのほかに，ばねやゴムひもでつるしたおもりの上下の振動，逆に下からばねで支えられている物体，例えば電車や自動車の車体の上下，左右への振動のように，弾性の力によって起こるものもある。またバイオリンなどの弦を弾いたり太鼓をたたいたりすると，弦や太鼓の膜が細かく震え動いているのが見える。これは弦や膜の各部分が，互いに隣接する部分に弾性の力を及ぼし合いながら振動して，全体としてある規則的な運動をしているのであるが，これを連続体の振動という。振動の特徴は，後で述べるように，物体が，それに働く力がつり合って静止する位置を中心として，その位置からずれるとそこへ戻そうとする力を受けて，周期的な往復運動を行う点である。ただし，物体が周期的に往復運動をしていても，振動とは呼ばない場合もある。例えば1台の電車が一定区間の線路の上で始発駅から終着駅までの間を繰り返し往復しても，その電車が振動しているとはいわない。一方，波動は振動と密接な関係をもつ。連続している物体の一部分に生じた振動が隣接している部分に次々に伝わっていく現象が波動である。以上では物体の運動の一形式としての振動について述べたが，もっと一般的に，ある量が一定の値を中心として，それより増えれば減らすように，またそれより減れば増やすような作用を受けて周期的に増減を繰り返すとき，これを振動と呼ぶ。振動は自然の中でしばしば見られる基本的な現象の型であり，その理論は種々の現象を理論的に解明する一つの重要な手法ともなっている。
→波動

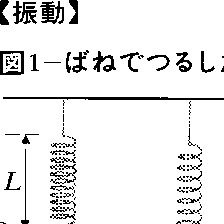
単振動

さまざまな振動の中でもっとも単純でしかも基本的なものが単振動である。具体的な例として，つる巻きばねでつるしたおもりの上下の振動を考えよう。図1のように自然の長さがLのつる巻きばねに質量mのおもりを静かにつるしたとき，ばねがx₀だけ伸びてつり合ったとする。x₀はフックの法則に従うばねの弾性の力kx₀（kはばねの定数）と，おもりに働く重力mgとのつり合いの条件，

　kx₀＝mg

から定まる。おもりをこの位置よりさらに引き下げて静かに放すと，上下の方向に振動を始める。ばねの伸びがxのとき，ばねに働く力は，上向きにばねの弾性の力f＝kx，下向きに重力mgである。図1のOの位置を原点とし，鉛直下向きを正の向きとしておもりの運動方程式を書くと，

となる。mg＝kx₀の関係を用い，またξ＝x－x₀と置くと方程式（1）は，

と書くことができる。ξはつり合いの位置O′を原点に選び直した場合のおもりの変位である。方程式（2）は，おもりに対してつねにつり合いの位置へ引き戻す向きに力が働き，その大きさはつり合いの位置からの変位ξに比例して大きくなることを示している。このような性質の力を受けて起こる振動を単振動，または調和振動といい，調和振動をしている物体を調和振動子と呼ぶ。

　さて方程式（2）に従う運動は時間tの関数，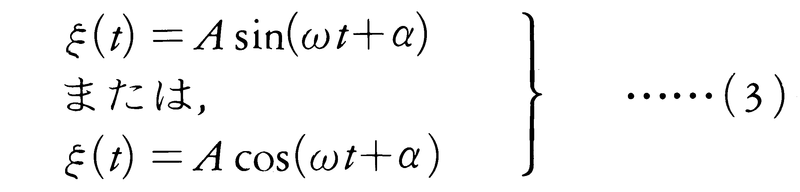

によって表される（）。このことは（3）を（2）に代入してみれば確かめることができる。正弦関数，余弦関数の周期性から，ξ（t）は時間がT＝2π/ωだけ経過するごとに同じ状態を繰り返す。Tを単振動の周期という。またν＝1/T＝ω/（2π）は1秒間に振動が何回繰り返されるかを示す量で，振動数と呼ばれる。Aはつり合いの位置からの変位ξの最大値を示すもので，振幅と呼ばれる。αはt＝0のときのξの値をきめる因子で，その値はおもりがどの位置にあったときから振動が始まったかによって定まる。αを初相という。なお，（ωt＋α）を振動の位相と呼ぶ。ω，T，νは働いている力の性質で決定されるが，Aとαは運動がどのように開始されたかによって決定される。

　方程式（2）に従う調和振動子は，運動エネルギーと，原点へ引き戻そうとする力による位置エネルギーをもっているが，その二つの和はつねに1/2kA²であるという性質をもっている。つまり調和振動子は一定のエネルギーを蓄えている。そのエネルギーは振動を開始させるときにおもりを弾いたり，ばねを引き伸ばしたことによって与えられる。

　単振動のもう一つの重要な点は，（3）では表せない周期的な運動を，（3）と同じ形でAやωの異なる式を数多く加え合わせることによって表すことができる点である。例えば図2のような関数f（x）は，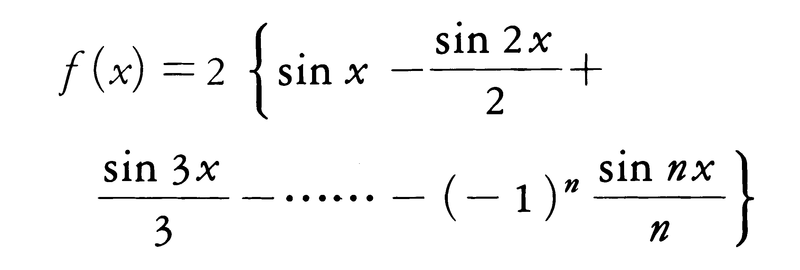

によって表すことができる。これをフーリエ展開という（フーリエ解析）。つまり複雑な周期的運動をいくつかの振幅・周期の異なる単振動を重ね合わせたものとして理解することができるのである。同様に，互いに直角な方向の単振動を重ね合わせると，平面上でさまざまな閉じた曲線を描く周期的な運動となる（リサジュー図形）。

　方程式（2）は右辺がξに比例する項だけを含んでいるが，自然現象の中には，右辺にξ²，ξ³などに比例する項も現れる方程式によって表され，単振動とは異なる特徴を示す振動の生ずる場合も少なくない。これを非線形振動，または非調和振動という。

電気振動

前にも述べたとおり，物体の運動以外にも振動の現れる現象は多く存在する。その中でもとくに電気回路に起こる電気振動は，通信機やラジオ・テレビの受信機などに利用され，技術的応用の面で日常生活に欠くことのできないものとなっている。電気振動の中でもっとも基本的なものは（2）式と同じ形の方程式で表されて調和振動を行う現象である。図3の回路で，電気容量Cのコンデンサーを充電したのちスイッチを閉じると，コンデンサーの極板上の電荷qに対して（2）とまったく同じ形の方程式，

が成り立ち（Lはコイルのインダクタンス），qは時間とともに，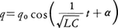

に従って変化する。このとき回路には周期的に変化する振動電流，

が流れる。

減衰振動

調和振動は，いったん振動を開始すると理論上はそれが永久に続くはずである。しかし実際に振子を振らせると，しだいに振れが小さくなって，やがて静止してしまう。これは方程式（2）の右辺に書かれている力のほか，振子に対して支点の摩擦や空気の抵抗など，運動を妨げる力が働くためである。電気振動の場合にも，方程式（4）では考慮に入れてない電気抵抗のために，振動電流はしだいに減衰する。いずれの場合も，抵抗に対して仕事をするために振動子のもっているエネルギーがしだいに失われていくのである。このようにエネルギーを失ってしだいに振幅が減少していく振動を一般に減衰振動という。減衰振動の中でもっとも簡単なものは，速さに比例する抵抗力を受ける場合で，運動方程式が，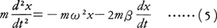

の形になるものである。右辺の第1項は（2）の右辺と同じで，もとに戻そうとする力，第2項が抵抗力である。ここでω²＞β²の場合，（5）の解は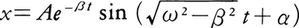，となり，振幅が指数関数的に減少する（図4）。ω²≦β²の場合は抵抗力の効果が大きく，運動は振動的にならない。

強制振動

減衰振動の場合とは逆に，振子に対して外から仕事をしてエネルギーを与えれば，振動はしだいに大きくなる。実際，静止している振子に周期的な力を加えると，たとえその力の大きさが小さくても，振子はしだいに振動を始め，振幅がだんだん大きくなっていく。これを強制振動という。とくにその振子の周期と等しい周期の力を加えると，もっとも効果的にエネルギーを与えて振動を大きくすることができる。この現象を共振という。外から加える力が周期的でなくても，エネルギーが供給されて振動が大きくなる場合もある。例えばバイオリンの弦は弓で一方向にこすることによって振動を起こす。このような現象を自励振動という。電気振動における自励振動は発振回路に利用されている。またぶらんこをこぐ動作は，外から力を加えずに振動を大きくしていく。この場合，ぶらんこに乗っている人が振動に合わせて足を伸縮させて重心を上下に移動させる動作が，単純化すれば振子の長さを周期的に変化させていることに相当し，重心を上下させるために人間は仕事をしなければならず，結局それが振子に与えられて振幅が大きくなっていく。このような現象をパラメーター励振という。

連成振動

図5のように振子のおもりを互いに弱いばねで連結したものや，振子のおもりにまた振子をつるしたものなど，二つ以上の振動系が相互に作用を及ぼし合いながら結合されているときの振動を連成振動という。図の例ではそれぞれの振子は互いに影響を与えながら複雑な振動をする。しかし特別な場合には，二つの振子がつねに同じ向きに，またはつねに逆の向きに運動するような振動が起こる。この場合，個々の振子の振動は簡単に（3）の形の式で表され，二つの振子の振動数も等しくなる（ただし，同じ向きの場合と逆の向きの場合とでは振動数が違う）。この振動を基準振動という。一般の場合にはこの二つの基準振動が重なり合って複雑な振動が起きるが，基準振動の考え方を用いるとその複雑な振動を明快に説明できる。振子の数が増えてn個になると，基準振動の数もn個になる。

連続体の振動

弾性体で作られた弦，棒，膜，板などの振動は，無数に多くの振子の連成振動と考えることもできる。すなわち弾性体の各微小部分が隣接する微小部分との間で互いに弾性の力を及ぼし合いながら振動をしているのである。またこれは弾性体内を伝わる波の定常波が成立している状態と考えることもできる。

　一例として，両端を固定し張力Tを加えて張った弦の振動を考えよう。この場合，弦に定常波ができているとすれば，両端は固定されているから必ず節となり，中間に腹が一つの場合，二つの場合，……が可能である（図6）。弦の長さをL，定常波の波長をλ₁，λ₂，λ₃，……とすると，

　λ₁＝2L，λ₂＝L，λ₃＝2/3L，……

で，一般には，

と書くことができる。弦の単位長さあたりの質量をσとすると，弦を伝わる波の速さvはで与えられることがわかっており，これと定常波の波長λ_n，振動数ν_nとの関係ν_n＝v/λ_nを用いると，

である。これらをこの弦の固有振動といい，とくにν₁を基本振動，ν₂以上を倍振動という。これらは先に述べた基準振動に対応するものである。例えば固有振動数ν₂の固有振動では，弦の各部分は弦と垂直の方向にそれぞれ振動数ν₂でいっせいに振動し，それぞれの振幅は図6のn＝2の場合の曲線で示されるように場所によって異なる。実際にはこれらの固有振動がいろいろの割合で重なり合った振動が起こる。

　管の中の気柱の振動，棒，板，膜などの面の振動も，同様の考え方で取り扱うことができる。板や膜の場合，定常波の節にあたる部分は面上の線となる。これを節線という。板の上に細かい砂などをまいておいて振動させると，砂が節線の部分に集まってその形を観察することができる。これはドイツの物理学者クラードニErnst Florens Friedrich Chladni（1756-1827）によって発見されたことからクラードニ図形と呼ばれている。
執筆者：有山 正孝

図1～図6

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

振動
しんどう
oscillation
vibration

糸でおもりを吊(つ)るした振り子が左右に揺れる運動や、つるまきばねの下端につけたおもりが上下に動く運動のように、位置や量が、ある時間ごとに繰り返し変化する現象。

［飼沼芳郎］

単振動

1直線上を運動する質量mの質点が、その直線上の原点からの変位xに比例する復元力F(x)＝－kx(k＞0)で原点に引かれる場合には、この質点の時刻tにおける変位x(t)はx(t)＝asin(ω₀t＋δ)で、質点は単振動をする（図A）。ここに、aは振幅、位相角(ω₀t＋δ)のω₀は角振動数で、ω₀＝2πν₀＝2π/Tである。ν₀は振動数、Tは周期である。このような復元力の場では、質点は位置のエネルギー(1/2)kx²をもつ。

［飼沼芳郎］

電気振動

コンデンサー（蓄電器）CとソレノイドLの両端を接続したLC回路に生ずる電気振動は、力学的な単振動に類似した現象である。ソレノイドの自己誘導係数Lは質点の質量mに、コンデンサーの容量Cの逆数は復元力の係数kに、コンデンサーの両極板の電荷、プラスQ、マイナスQのQは質点の変位xに、電流Iは質点の速度vに、それぞれ対応する（図B）。また、コンデンサーの両極板間に生ずる電場のエネルギーは質点の位置エネルギーに、ソレノイドに流れる電流のつくる磁場のエネルギーは質点の運動エネルギーに対応する。このような対応関係をみれば、LC回路に電気振動が生ずるのは当然のことであると理解できるであろう。

［飼沼芳郎］

減衰振動

実際には、質点に抵抗力が働き、振動はしだいに減衰して、ついには静止する。抵抗力が質点の速度に比例する場合には、振動を繰り返すたびに、振幅が指数関数的に減少する。このような振動を減衰振動という。電気振動においても、回路に電気抵抗Rが直列に接続されたLCR回路では、減衰振動がおこる。

［飼沼芳郎］

強制振動

外力が質点に働かぬ場合の振動を自由振動という。自由振動としては減衰振動をする質点に、時間とともに振動的に変化する外力が働き、押したり引いたりを繰り返す場合には、最初の過渡的な振動が減衰したのち、質点は外力と同じ振動数で振動する。これを強制振動という。強制振動において、外力が質点に単位時間にする仕事、すなわち質点が単位時間に吸収するエネルギーの平均値は、外力の振動数が質点の固有振動数（抵抗力ゼロのときの単振動の振動数）に等しいときに最大になる。これを共鳴、または共振という。直列のLCR回路を交流電源に接続した場合にも、電気振動の強制振動がおこる。

［飼沼芳郎］

連成振動、連続物体の振動

水平に張った糸に、おもりの質量も糸の長さも等しい二つの振り子をつけて振動させる。二つの振り子の間には相互作用があり、各振り子の振動は独立ではない。このような種類の振動を一般に連成振動という。この二つの振り子が同一方向に振れるような型、および反対方向に振れる型の振動は互いに独立であり、時間が経過しても振動の様態に変化がない。このような振動を基準振動または固有振動といい、その振動数は基準振動数または固有振動数とよばれる。

　連続物体の振動には、支持方法などによって規定される境界条件を満たすような基準振動の型が無数に現れる。この基準振動は連続物体を伝わる波の重ね合わせによって生ずる定在波の振動ともみなされる。基準振動をしている連続物体には振幅最大の腹(はら)の場所と、振幅ゼロの節(ふし)、節線、節面がみられる。連続物体の振動の例としては、ピアノや琴の弦のような両端を固定した弦の横振動、太鼓やドラムの皮のような周囲を枠に固定した膜の振動、木琴のように両端が自由な棒の曲げ振動、つるまきばねの縦振動、オルガンのように一端が閉じ他端が開いた管内の空気柱の振動、クラードニの方法（板の中央とへりの1点を固定し、板のへりをバイオリンの弓でこする方法）による板の振動、音叉(おんさ)の共鳴箱の中の空気の振動、空洞共振器内におけるマイクロ波領域の電磁波の振動などがある。音叉は曲げた棒のような振動をし、その下部は振動の腹になる。鐘は曲げて絞った板のような振動をし、振動の節線が鐘の頂点を通る鉛直面上に現れる。

　上端を固定して吊るした針金の軸の周りのねじれ変形の振動、すなわちねじれ振動は、たとえば金属の剛性率（ねじれの弾性率）の測定に用いられる。針金のねじれを利用して微小な力を測定するねじれ秤(ばかり)が、キャベンディッシュの万有引力法則の実験や電気のクーロンの法則の実験に用いられたことはよく知られている。ねじれ秤の針金に働く偶力のモーメントとねじれ角の比の決定にもねじれ振動が用いられた。

［飼沼芳郎］

非線形振動

振動の運動方程式が、変位、速度、加速度などの一次式では表すことができぬ場合の振動を非線形振動という。振り子の振れ角が大きい場合には、復元力が振れ角に比例するという近似を使用することができなくなる。この場合には、振り子の振動の周期は振幅とともに増大し、単振り子の等時性が失われる。ぶらんこの振動は、これに乗ってぶらんこをこぐ人の重心が周期的に上下することによって励起される。これは振り子の糸の長さが周期的に変化することに相当する。糸の長さのように振動を決定するパラメーターを時間的に変化させることによって振動をおこすことをパラメーター励振という。弦の横振動には、弦の張力を周期的に変化させて振動を励起するメルデの実験がよく知られているが、これもパラメーター励振である。バイオリンの弦に弓を押し付けて引くと弦が振動する。チョークで乾いた黒板に線を引くとき、きしんで点線が描かれることがある。これらは、それ自身は振動的でない原因によって持続的な振動がおこるものであり、自励振動とよばれる。いずれの場合にも、二つの物体の相対速度が大きくなると摩擦力が減るという乾性摩擦の性質に関係する。このような摩擦力は負抵抗として働く。普通の正の抵抗が働くと、振動の力学的エネルギーは失われるが、負の抵抗が働くと、力学的エネルギーが外部から供給されて、たとえば図Cに示すように振動が成長し振幅が大きくなる。九州の大分県日田(ひた)市の小鹿田(おんだ)焼の陶器にとびがんなの刻み目をつけるときにも、ろくろの上で回転する生乾きの皿などに金鋸(かねのこぎり)の刃のような薄く弾力的な金属板（かんな）を押し付けたときにおこる自励振動が用いられている。日本式庭園などにみられるししおどし、添水(そうず)は、竹筒の一端を斜めに切り、筒の中央を水平な軸で支え、懸樋(かけひ)の水を竹筒に受け、水がたまると重心が移動して竹筒が傾いて水を吐き出し、元の位置に戻るとき、竹筒の底が石を打って鋭い音を発するものであり、以後このような振動が繰り返される。このような振動は緩和振動とよばれる。ネオン放電管とコンデンサーCを並列につなぎ、これを抵抗Rを通して直流電源につないだ回路では、緩和振動がおき、時間とともに鋸歯状に変化する電圧が発生する（図D）。ネオン管の放電が停止している間は、コンデンサーに充電が続けられ、その両極板間の電圧がネオン管の放電電圧に到達すると、ネオン管が放電して、電圧が一挙に低下し、放電が停止する。以後これが繰り返される。

　連続物体の振動においても、その振幅が十分に小さくないときには、しばしば非線形振動がおき、物体のさまざまな基準振動は互いに独立ではなくなり、それらの基準振動の間に相互作用が生ずる。

［飼沼芳郎］

[参照項目] | 共振 | 減衰振動

質点の単振動〔図A〕

LC回路に生ずる電気振動〔図B〕

振動の成長〔図C〕

緩和振動〔図D〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

振動
しんどう
oscillation; vibration

振り子のふれ，おもりをつるしたゴム紐の伸縮運動のように，安定な平衡点をはさんで周期的に位置が変化する運動。振動は，平衡点の正負どちらへ位置をずらせても平衡点に向って戻る復元力が働く系に変位 (位置のずれ) を与えたときに起る。空間を伝わる振動を波または波動という。最も基本的な振動は変位の時間変化が正弦関数で表わされる単振動であって，一般の周期的振動はフーリエ分解によっていくつかの単振動の重ね合せで表わされる。
振動系はその構造によって定まった固有振動をもつ。振動系に復元力だけが働くときには自由振動，抵抗などのように振幅を減少させる制動力も働くときには減衰振動が起る。さらに周期的な強制力が加わると強制振動が起り，強制力と固有振動との振動数が一致すれば共振 (→共鳴 ) が生じる。また，2個以上の振動系を結合させれば連成振動を生じる。弦，膜，板，棒などの物体は無限に多数の質点の集合体であるから，その弾性振動は個々の質点の振動が連成して生じた複雑な振動である。この振動の様子の違いが種々の楽器の音色の違いを生じる。複雑な周期振動はフーリエ分解して，ある振動数の基本振動とその倍振動との和の形に表わせる。これを振動の調和解析という。さらに拡張して，任意の物理量が周期的に変動する現象を一般に振動という。電気振動などはその例である。
力学系の振動，弾性振動，音響振動，電気振動などは類推によって統一的に理解できる。たとえば，弾性振動する弦や膜から音波が放射されるように，振動する電荷から電磁波が放射される。また，音波が共鳴箱に共振してとらえられるように，電波はアンテナ回路に共振して受信される。分子や結晶などの内部の熱運動は大部分が構成原子やイオンの平衡位置近くで行う振動であって，熱振動と呼ばれる。熱振動を量子力学で扱うことによって，比熱などの物質の性質が理解される。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

振動【しんどう】

物体の位置，電流の強さなどの物理量が一定時間（周期）ごとに一定の（減衰振動などではほぼ一定の）値をとるよう，規則正しく変動すること。振動するものを振動体といい，その種類により弾性振動，電気振動などがある。振動はふつう外からの物理的刺激によって起こるが，その刺激がなくなった後も続くものを自由振動または固有振動，周期的な外力の作用の下で続くものを強制振動という。最も簡単な振動は単振動で，一般の振動は幾つかの単振動の組合せとして表現でき，周期または振動数，振幅などの量で特徴づけられる。→振動計
→関連項目環境破壊｜共鳴｜公害｜公害対策基本法｜公害病｜産業公害｜チリ地震｜都市公害

出典　株式会社平凡社

普及版 字通

【振動】しんどう

振るい動かす。〔墨子、尚同中〕數千里の外も、不善を爲す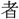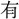らば、～天子得て之れを罰す。是(ここ)を以て、天下の人を擧げて皆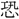懼し、振動し、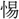慄(てきりつ)し、敢て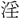暴を爲さず。

字通「振」の項目を見る。

出典　平凡社「普及版 字通」

知恵蔵

振動

「騒音」のページをご覧ください。

出典　(株)朝日新聞出版発行「知恵蔵」

世界大百科事典（旧版）内の振動の言及

【極限】より

…(2)同様に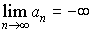の場合が定義される。(3)その他の場合，その数列は振動すると呼ばれることがある。実数列が収束するために必要十分な条件は，それが基本列をなすことである。…

【数列】より

…もしも，nが限りなく大きくなるとき，a_nが限りなく大きくなるか，または－a_nが限りなく大きくなるならば，この数列はそれぞれ正の無限大に定発散する，または負の無限大に定発散するといい，このことを，それぞれ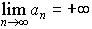または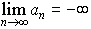と書く。その他の場合は，数列は不定発散する，または振動するという。定発散と不定発散とを合わせて単に発散という。…

【発散】より

…収束と定発散の場合は，極限があるという。極限がない数列は不定発散する，または振動するという。例えば数列｛n｝，｛－n｝は定発散であり，数列｛(－1)ⁿ｝，｛(－1)ⁿn｝は不定発散である。…

【触覚】より

…19世紀に触，温，冷，痛覚に対応する感覚点sense spotが発見され，以来触覚が温，冷，痛の諸感覚からより明確に分離されるようになった。
［触覚と刺激］
　変形が1回かぎりであればそれは軽い一過性の接触の感じをおこすが，これがある頻度(10回/秒以上)で繰り返されると振動感覚vibrationを生じ，変形が一定時間以上持続するときには圧覚pressureを生じる。接触の感じは，局所的な圧迫によって皮膚がへこんだときおこるほか，たとえば皮膚に接着した物体を介して皮膚が軽くひっぱり上げられても生じる。…

【地下鉄道】より

…　軌道は，運転頻度の高い列車を対象に，建設費の節減と保守作業の軽減を図るために，軌道構造の強化，簡素化が行われており，道床をコンクリートでつくったり，あるいはレールを道床に直接締結する方式などを採用している場合が多い。また後述するが，電車通過時の騒音，振動対策もとられている。日本の地下鉄の軌間は，狭軌(1067mm)と標準軌(1435mm)がほとんどであるが，東京都営新宿線の1372mmや札幌のゴムタイヤ軌道(南北線，ゴムタイヤ中心間隔2300mm)もある。…

※「振動」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」