翻訳|mathematics
精選版 日本国語大辞典 「数学」の意味・読み・例文・類語
すう‐がく【数学】
- 〘 名詞 〙
- ① 天文・暦法を含めた陰陽・五行・卜占の術の総称。術数の学。
- [初出の実例]「附下之好二陰陽数学一者上可。非二儒者之先務一」(出典:童子問(1707)下)
- [その他の文献]〔
 文豹‐吹剣四録〕
文豹‐吹剣四録〕
- ② 主として、数量および空間の性質について研究する学問。算術・代数学、幾何学、解析学、ならびにそれらの応用の総称。
- [初出の実例]「所詮は楽二数学一永々繁昌」(出典:算爼(1663)四)
- 「字を書くのと数学(スウガク)を覚ゑるのは孰(いづ)れが難いか」(出典:花間鶯(1887‐88)〈末広鉄腸〉緒言)
- ③ =すうがくか(数学科)①
- [初出の実例]「譬へば爰に数学の教師あらん」(出典:文明論之概略(1875)〈福沢諭吉〉三)
- ④ =すうがくか(数学科)②
- [初出の実例]「長兄繁(二四)は現に理科大学に通学して数学を専攻し」(出典:都新聞‐明治三九年(1906)一一月一四日)
数学の語誌
一九世紀に入って中国の洋学書などで mathematics の訳語として用いられた。明治初期に算数、幾何学、代数などの総称として次第に「算数」と使い分けられるようになり、数多く出版された漢字字書や外国語辞書にも採用され、一般化した。
改訂新版 世界大百科事典 「数学」の意味・わかりやすい解説
数学 (すうがく)
mathematics
今日の先進文化圏の日常生活は本質的に科学技術に依存している。それをさほど目だたぬところで背後から支えているのが数学である。例えば都市生活の基盤となっている電気,ガス,水道,道路,あるいは鉄道,自動車,航空機などの交通機関,電話,テレビなどの通信機関,人工衛星やコンピューターなど,いずれも数学を用いずに設計製作することはできない。数学はこのように文化生活の基礎をなすものであるが,それ自身高度な学問として研究され,世界の数学者の協力により絶えず進歩を続けている。どのような歴史を経てこの学問がつくられ,どのような性格のものに今日なっているかを以下に概観しよう。
数学の発祥--ギリシアの数学
エジプトやバビロニア,あるいはインド,中国など,古くから文化の進んだところでは,行政上の必要などから数や図形に関する知識が得られ,それ自身の興味のためにも研究された跡がある。ことにバビロニアの知識は進んだものであったことが,1930年代からの研究で明らかにされた。しかし学問としての数学が初めてつくられたのは古代ギリシアにおいてである。古代ギリシアの文化は前十数世紀から後6世紀ころまで続き,地域的にも地中海沿岸の全域にわたっていた。前4世紀のプラトン,アリストテレスの時代,それに続くアレクサンドロス大王の時代に,それぞれ文化的,政治的な頂点をもつ。数学に関しては前6世紀のタレス,ピタゴラスに始まる多くの名が挙げられるが,そのうちでも前3世紀のユークリッド(エウクレイデス)およびアルキメデスは重要である。
ユークリッドの主著《ストイケイア(原論)》(13巻)は,幾何学に関する内容が多いので,《幾何学原本》とも呼ばれているが,数論や実数論をも扱っており,それまでに得られていたギリシア数学の成果を体系的に集大成したものである。当時の文化の中心地であったアレクサンドリアの学問の殿堂ムセイオンで教科書のようにして用いられたようで,多くの写本が残され,19世紀の数学史家によってほとんど完全と思われるテキストが復元された。開巻第1ページには〈点は部分のないものである〉というような定義があり,〈要請〉(あるいは公準)と〈共通概念〉が続く。要請のうちには〈一つの直線が二つの直線と交わり,その一方の側にできる二つの角の和が2直角より小さいときは,その側に二つの直線を限りなく延長すれば,必ず交わる〉というのがある。これは1直線外の1点を通って,それに平行な直線は一つしかないという命題(いわゆる平行線の公理)と同値であり,後に問題となるものである。共通概念は〈同じものに等しいいくつかのものは,互いにも等しい〉というようにだれにも共通に認められていることで,一般公理とも呼ばれる。それに対して公準は幾何図形に関するものなので,幾何学公理とも呼ばれることがあるが,両者ともに理論の出発点として成り立つことを認める(あるいは要請する)ものである。それを公理というのである。《ストイケイア》は定義と公理とだけから出発し,厳密な論理によって全体系を構成しようとしている。その厳密性には実は,多少の欠陥があり,後に補われることとなったが,そこで意図されていた〈はっきり言明された基礎,すなわち定義と公理によって論理的に構成された体系〉こそが今日の意味でも数学の実体である。《ストイケイア》の方法はその後長く学問一般の模範とされるようになった。
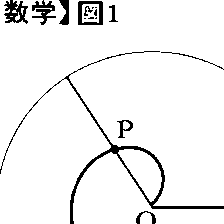
《ストイケイア》の内容をみると,1~6巻は直線図形や円に関する平面幾何学であるが,第5巻は比例論(あるいは実数論)を扱っている。7~9巻は数論で,最大公約数を見いだすユークリッドの互除法や,素数が無限にあることの証明などを含んでいる。第10巻は平方根をとることによって得られる無理数の分類論である。11~13巻は立体幾何学で,5種の正多面体についての記述で終わっている。《ストイケイア》には,円周の長さはその半径に比例し,円の面積はその2乗に比例することが証明されているが,円周率の値については何もいっていない。アルキメデスはそれが31/7と310/71の間にあることを証明している。また点Oを一端とする線分OAがOのまわりに等速度で回転するとき,OAの上をOからAの方向へ等速度で動いていく点Pはアルキメデスの螺線(らせん)を描くが,線分が1回転する間に描くその螺線OPAとOAで囲まれる面積は,OAを半径とする円の面積の1/3に等しいことなども示している(図1)。このような運動学的な考察は《ストイケイア》には見られないところで,こうした求積問題の解法は後の積分法の原型とも見られる。しかもアルキメデスは,単にこの結果を述べるだけでなく,〈二つの量a,bがあるとき,自然数nを十分大きくすれば,na=a+……+a(n回)はbより大きくなる〉(アルキメデスの原理と呼ばれる)を用いてそれを証明しているのである。アルキメデスにはなお静力学あるいは光学上の発見や技術的な発明もあるが,彼自身はそれよりも理論的な研究を重んじたとプルタルコスは記している。当時のギリシアの価値観には,そうした傾向があったのである。
ギリシアには後にも円錐曲線を扱ったペルゲのアポロニオス,正弦の表をつくり惑星の運動を記述したプトレマイオス,記号代数を用い始め,数論の問題を扱ったディオファントスなどの数学者があり,それぞれ後世に影響を及ぼしている。
代数学の起源--アラビアの数学
前1世紀に帝政ローマが成立し,ギリシア文化圏も政治的にはその制圧下におかれた。ローマ人は実際的で,政治,軍事,土木建築に長じたが,数学上の独創は見られなかった。7世紀から12世紀にかけ,アラビアにイスラム文化が栄え,ギリシアの科学や文化は,そこで継承されることになる。ユークリッド,アルキメデス,アポロニオスなどの諸著作もアラビア語に翻訳されて学習された。他方アラビアは東方の国々にも接している。ギリシアでは上述のように理論的な数学が進歩したが,記数法が不便であり,計算技術については古くから十進法を用い,空位を表す0をも知っていたインドに及ばなかった。9世紀のバグダードで活動したフワーリズミーは,インド数学の影響を受けた計算法や代数学の書物を著し,一次方程式や二次方程式を解く算法を記述した。代数学の原語algebraはその書名に由来しており,算法を意味するアルゴリズムalgorithmもフワーリズミー(アルは冠詞)の名を語源としている。さらに12世紀の詩人ウマル・ハイヤームは天文学者,数学者でもあり,改暦に従事し,代数学の書を残した。それには円錐曲線の交点を用いて三次方程式を解く方法が述べられている。8世紀にはイスラム文化は地中海東部よりスペインにも及ぶようになるが,11世紀より13世紀にかけ,キリスト教徒は十字軍を組織して東方に遠征し,そこでも東西文化の接触が起こる。13世紀のフィボナッチ(ピサのレオナルド)は東方に旅行したイタリアの商人であるが,アラビアで行われていた計算技術や代数学を含む《算盤の書》(1202)を著した。そのころから代数学がイタリア,ついでヨーロッパ全土に知られ,漸次発達するようになる。16世紀のイタリアでは三次方程式,四次方程式の解法も得られる。今日世界的に用いられているアラビア数字は,インド起源のものであるが,そのころアラビアを経由してヨーロッパに伝わり,その後多少の変遷を経て,現在の形になったのである。
中世~近世の数学
西洋の5世紀から15世紀ころまでの中世は,キリスト教の影響が強かったが,戦争が絶えず,学問が保たれたのはほとんど修道院の中に限られた。12世紀以降,ボローニャ,パリなどに大学ができ,そこで学ばれたのも神学やスコラ哲学を主としていた。自然科学では,アリストテレスの諸著やユークリッドの最初の部分などが学ばれた。その間にも,ときには無限についての考察がなされ,イギリスのR.ベーコンは数学が重要な学問であることや,自然学の研究では実験がたいせつであることを説いた。リジューの司教となったニコル・オレームNicole Oresmeが温度の変化をグラフに表したり,分数指数を導入したりしたのは,当時としては先端的な発想であった。対数が発見されたのは16世紀の中葉になってからイギリスのJ.ネーピアやブリッグスHenry Briggs(1556-1631)によるもので,ブリッグスは後述するケプラーの計算にも協力した。
13世紀のイタリアには,ダンテらによってルネサンスの機運が興り,美術上のルネサンスは15~16世紀に最盛期を迎える。14世紀以降,中世の終りを告げるといわれた航海用羅針盤,火薬,印刷術の発明があり,15世紀の終りにはコロンブスが新大陸を発見する。鉱山業,織工業などの生産手段には機械が導入される。レオナルド・ダ・ビンチは絵画,彫刻,建築などあらゆる方面に天才を発揮し,透視法,航空術,解剖学など科学技術についても先駆的な考えを示す。M.ルターが宗教改革を開始したのは1517年であった。43年は,N.コペルニクスの《天球の回転について》とA.ベサリウスの《人体の構造》が発表された年である。それぞれ近代的な天文学,解剖学の出発点となったものであるが,数学に関係するのはとくに前者である。
星の運行を説明するのに,古代ギリシアでは天動説と地動説があった。両方ともピタゴラス学派のいうとおり,天球が一定速度で回転するとしたのであるが,前者は回転の中心は地球であって太陽がそのまわりを動くとするのに対し,後者は太陽を中心として地球が動くとするのである。前者はアリストテレスの主張したところで,惑星の運動に関するプトレマイオスのかなり精密な記述もそれによっていた。それはキリスト教の人間中心観とも合致し,中世を通じて権威とされていたが,すでに前3世紀のサモスのアリスタルコスは地動説をとっていた。コペルニクスはポーランドに生まれ,イタリアの大学で神学,医学,数学,天文学などを学び,そのとき地動説のことも聞いたのであろう。故郷に帰って聖職につき,医療にも従事していたが,天文学に深い興味を抱き,プトレマイオスの記述を地動説に従って書き直してみるとより簡単になることに気づいた。それは当時の権威に反することであったので,コペルニクスはその発表に積極的でなかったが,人にも勧められて書きまとめたのが,彼の死と同年に発刊された上述の著書であった。
この書にはコペルニクス自身の観測の結果も記されているが,その数は少ない。彼はむしろ理論家であったが,デンマークの天文学者T.ブラーエはすぐれた実験家であった。彼は当時としてもっとも精密な天文観測を続けて行い,その結果を記録した。《世界の調和》(1619)に絶大の信念をもったJ.ケプラーは,地動説にもとづき,ブラーエの観測結果を分析して,ケプラーの三法則を得た。その第1,第2法則(1609)は,惑星は太陽を1焦点とする楕円軌道上を,一定の面積速度で運行するというもので,第3法則(1619)は,惑星の公転周期の2乗は,軌道の長軸の長さの3乗に比例するというのである。ここに現れた楕円に関する計算には,アポロニオスの円錐曲線論が用いられている。この理論は自然現象の解明に役だてることなどはまったく考えずに幾何学的につくられたのであるが,千数百年後にこのように有効に用いられたのである。
G.ガリレイはコペルニクス,ケプラーの地動説を強く支持し,宗教裁判にかけられたことが知られている。彼は自然科学は実験と数理にもとづくべきで,権威によるべきではないと主張した。彼の晩年の著《新科学講話》(1638)は,新しい力学の基礎を定めたものとしてとくに重要である。ケプラーやガリレイの活動したのは,17世紀に入ってからであった。この世紀は,数学史上,〈英雄の世紀〉とも呼ばれる著しい時代である。
17~18世紀の数学
16世紀のイタリアでは代数学が進んで,三次や四次の代数方程式の解法が得られたことを前に述べたが,それをさらに発展させ新しい時代の代数学を基礎づけたのは,フランスのF.ビエトであった。彼は記号代数を推進し,ことに既知数をも記号で表し,四次までの代数方程式の解法を一般的に述べた。代数計算によって,数学理論を構成するのは,そこから始まったのである。P.deフェルマーは,代数的方法を駆使して,ディオファントスの数論を発展させ,また曲線の接線を求めることや,最大最小の問題を扱い,光学にも応用した。またB.パスカルとの往復書簡では確率論の先駆となった問題を論じた。パスカルには円錐曲線論,流体静力学,サイクロイドに関する求積問題などについての業績があるほか,数学的帰納法を自覚して用いたことも著しい。パスカルは晩年書き残した宗教的断章によって知られる思想家でもあった。
しかしこの世紀の数学史,科学史上のもっとも大きな人物としては,R.デカルト,I.ニュートンおよびG.W.ライプニッツを挙げるべきであろう。
デカルトは,近世合理主義の基礎を定めた哲学者である。主著《方法序説》(1637)の付録の一つとして《幾何学》を著し,今日のことばでいえば平面上の座標を用いて代数曲線を扱うことの有用性を力説した。この方法は実質的にはアポロニオスが円錐曲線についてすでに用いていたものであるが,ギリシアの幾何学とともに,ビエトの代数学を併用して,数と空間とを融合する考えを述べたのは,それからの数学に大きな影響を与えた。
ニュートンは,光学への著しい貢献もあり,化学や神学にも深い関心をもったが,主著《プリンキピア》(1687)において,それ以後の科学的自然観の基礎となるニュートン力学を展開したことの意義が大きい。アリストテレスは,力の働かない物体は静止しているとしたが,実は等速運動を続けるのであり,力は加速度を与えるものであることを見抜いたのはガリレイであった。地球上の物体には一定の重力が働く,ということによってガリレイは落体の運動を説明したが,ニュートンはさらに万有引力の法則によって惑星の運動も説明され,ケプラーの三法則も数学的に証明されることを示したのである。加速度は物体の位置を時間の関数として表すベクトルの二次微分で表されるから,これは今日のことばでいえば2階の微分方程式を積分することに当たる。そのような表現ができ,問題が解決されるためには,まず微積分法がつくられねばならない。ニュートンはそれをも同時に成し遂げたのである。
ライプニッツは,神学,哲学,数学,歴史学など万般の学に寄与したうえ外交官として政治活動をもした人である。数学ではとくに記号の重要性を力説し,ニュートンとほとんど同じころ微積分法を発見して,適切な記法を導入した。今日も用いられている微分の記号d/dx,積分の記号∫は彼に負うものである。関数functionの語を今日のような意味に用い始めたのも彼であった。
ギリシア以来の幾何学,インド・アラビア系統の代数学に加えて,関数を扱う解析学が17世紀後半には誕生したのである。次の世紀には,その研究が順調に進み,自然科学の各方面に広く応用されるようになる。
18世紀の初めには,ニュートンやライプニッツも活動していた。ライプニッツの便利な記号による微積分法は,ベルヌーイ兄弟らの協力によって幾何学,力学あるいは確率論の多くの問題に応用され,彼らに続くL.オイラーによりさらに発展させられた。オイラーは古今を通じもっとも多産な数学者の一人であり,代数計算にはことに巧みであった。数論,幾何学,力学のあらゆる方面で活躍し,解析幾何学や解析力学を今日の教科書に見られるのと近い形に整備した。彼の著書の一つは《無限解析序説》(1748)と題されている。その書では複素数を項とする無限級数も用いられ,指数関数と三角関数の関係などが明らかにされている。
L.オイラーはベルヌーイ家と同じく,スイスのバーゼルの出身であるが,当時の開明君主といわれたドイツのフリードリヒ大王やロシアのエカチェリナ女帝の庇護を受けてベルリンやペテルブルグのアカデミーでその生涯を送った。この人たちの数学的な寄与によって科学技術が進展し,それによる生産手段の改善が顕著となり,人々は理性への自信をもち始めた。18世紀は〈光の世紀〉とも呼ばれる。フランスではけんらんたるルイ14世時代が過ぎ去った後,J.ダランベールらを中心とする百科全書派が活躍し,やがて1789年のフランス大革命を迎える。
P.S.ラプラスは,王政末期から革命時代,ナポレオン時代,さらに王政復古の時代にかけていつも高い地位にあり,政治的節操には欠けるところがあったが,18世紀解析学の頂点をきわめた数学者である。彼は5巻の《天体力学》(1799-1825)と《確率の解析的理論》(1812)を残した。前者はポテンシャル論を含み,ニュートン,オイラーらにもとづく太陽系の理論をまとめたもの,後者はラプラス変換論や生成関数論を含む大著である。彼にはまた両著の内容を数式を用いずに解説した啓蒙書もある。そこには数理解析により,世界のすべてのことが機械的に決定されるはずであるという考えへの深い信頼が表明されている。
19世紀以降の数学
J.L.ラグランジュはラプラスと同時代の数学者で,《解析力学》(1788)や《解析関数論》(1797)などの著書で知られるが,彼は18世紀末には,数学にはもうこれ以上本質的な進歩はありえないかのように思っていたという。しかし世紀の移るころからまったく新しい数学の傾向が見られるようになった。一つは批判的精神であり,もう一つは純粋数学への志向である。社会的には産業革命が定着して資本主義社会が到来したこと,フランスでは何回も政変があったが,フランス革命期にエコール・ポリテクニクやエコール・ノルマル・シュペリウールのような学校ができ,ドイツにもゲッティンゲンなどに大学ができるようになったことなどの影響もあったのであろう。
権威に対する批判の精神は17世紀のガリレイらにも見られるところであるが,17~18世紀の解析学は基礎の論理性に関してはむとんちゃくであった。ニュートンの《プリンキピア》はユークリッドの《ストイケイア》の形式を模して書かれたけれども,ギリシア的厳密性をまったく欠いていた。それは同時代の人からも批判されていたが,解析学が多くの実際問題に応用されて華々しい成果を収める間に,基礎の検討は忘れ去られたようである。無限級数の収束,発散を確かめずにその和について語るようなことを,オイラーやラプラスなどもすることがあった。19世紀初頭,アカデミー・デ・シアンスで,A.L.コーシーが〈収束しない無限級数は和をもたない〉という今日から見れば当然のことを述べたとき,ラプラスは衝撃を受けたと伝えられる。関数の連続性,微分可能性,積分可能性などの定義が与えられたのも19世紀になってからである。
このような厳密性の追求は,この時期の批判精神の現れでもあるが,また直接の応用にはつながらない点で,純粋数学への志向の一面とも見られる。18世紀にはほとんどすべての数学者が応用に携わり,功利主義的な数学観が支配していたが,19世紀には〈ギリシアへの復帰〉の機運が見られるようになったのである。
C.F.ガウスは両世紀の境界に立つ数学者である。彼はゲッティンゲン大学の天文台長となって,みずから観測にも従事して,天文学,測地学,電磁気学など数学の応用にも著しい功績があったが,それに関連して最小二乗法を数学的に基礎づけたり,曲面論,ポテンシャル論を展開するなど,純粋数学の新生面をも開いた。彼は19歳のとき,正十七角形が定規とコンパスで作図できることを発見して数学者となる決意をしたといわれる。ディオファントス,フェルマー以来の数論は彼の《数論研究》(1801)によって一時期を画された。数論はいうまでもなく純粋数学の一分野であるが,ガウスはそれを〈数学の女王〉と呼んだ。
G.F.B.リーマンは19世紀前半より中期にかけてのもっとも重要な数学者である。彼は電磁気学や熱伝導論など理論物理学への寄与もあるが,複素変数の解析関数論,ことに代数関数論の基礎を定め,積分論や三角級数論にも重要な貢献をし,数論上古くからのなぞとされた素数分布の問題を扱うのに,ゼータ関数を複素変数の関数として考えるという新しい方法を創始した。このように純粋数学の多くの分野にそれぞれ独創的な貢献をしたが,1854年ゲッティンゲン大学の就任講演《幾何学の基礎をなす仮説について》はとくに重要である。
その前にガウスは彼の《曲面論》(1827)で十分滑らかな曲面の等長変換(長さを変えない変換)によって変わらない性質を論じ,とくに曲面上の各点の全曲率がその性質をもつことを示した。さらに,そのような曲面上に測地線を辺とする多角形が描かれていれば,その内部の点における全曲率を積分したものは外角の和(図2の例ではα1+……+α5)と4直角との差に比例することを証明した。平面上の三角形の内角の和が2直角であることや,球面三角形の内角の和は2直角より大きく,それと2直角との差(球面過剰)はその球面三角形の面積に比例することは,その特別の場合と考えられる。リーマンはその考えを二次元の曲面の場合から,n次元の多様体の場合へ拡張した。そこでリーマン多様体が定義され,いろいろな幾何学が成り立ち得ることを示したのである。
ユークリッドの《ストイケイア》に展開された幾何学は,中世を通じて権威とされ,カント哲学では先験的なものとさえされたが,19世紀にはそれも批判精神の対象とされる時代となった。《ストイケイア》では平行線の公理が複雑な形に述べられ,なるべく使うのを避けていたように見られるので,それを他の命題でおきかえ,《ストイケイア》の他の命題から導こうとする試みは古くからなされた。しかしこの公理が真理であることに疑いをもつ者はなかった。批判精神の盛んな時代となり,曲面の幾何学を考えているうちにガウスは,あるいは現象空間において,1直線外の1点を通りそれに平行な直線がただ一つではないこともありうるのではないかと思い,その仮定の上に成り立つ幾何学の研究を始めた。彼は世人の無理解をおそれてそれを発表しなかったが,同時代のボーヤイ J.やN.I.ロバチェフスキーはその研究を公表した。上の仮定のもとでは三角形の内角の和は2直角より小さくなるが,球面幾何学と多くの類似点をもつ幾何学が構成されることが示されたのである。このように平行線の公理を否定した命題を仮定した幾何学を非ユークリッド幾何学といい,それに対して《ストイケイア》に見られるような幾何学をユークリッド幾何学という。ガウス自身大きな三角形について実測し,その内角の和と2直角との差を調べたが,それは誤差の範囲内にあって,現象空間でどちらの幾何学が成り立つかについての結論は得られなかった。いずれにしても,非ユークリッド幾何学がユークリッド幾何学と同様に成立することは,〈公理は真理である〉という考えを覆すこととなる。平行線の公理Eとそれを否定したものĒとはもちろん両立しない。現象空間で成り立つことを真理というならば,どちらが真理であるかは観測によって確かめねばならない。観測でどういう結論が得られるかは,幾何学に内在する論理とは関係のないことである。ユークリッド幾何学の公理のうち,平行線の公理を除いたものをAとすれば,両方の幾何学が成立するというのは,AとEも,AとĒもともにそれぞれ矛盾を含まないことを意味する。このことの意味をはっきりさせるためには,上のAの内容を明らかにせねばならないが,それも19世紀の数学者たちに待たなければならなかった。ユークリッドの《ストイケイア》は,論理的に多くの欠陥を含みその点が明らかにされていなかったからである。D.ヒルベルトの《幾何学基礎論》(1899)はユークリッド幾何学の公理を5群にわけて完全に与え,その間の論理的関係を精密に調べた。《ストイケイア》はそこで初めて意図されていたとおりに整備され,明示された前提から,厳密な論理によって構築された体系として再現されるにいたったのである。
そのような体系が成立するためには,まず第1に無矛盾でなければならない。ユークリッド幾何学,非ユークリッド幾何学がともに成り立つというのは,(A,E),(A,Ē)とも無矛盾であるという意味であった。(A,Ē)の無矛盾性が確認されたのは,そのモデルが(A,E)の中につくられることがA.ケーリー,F.クライン,H.ポアンカレらによって示されたからである。ヒルベルトはさらに実数を用いて(A,E)の諸命題が成り立つモデルをつくり,(A,E)の無矛盾性を示した。実数論については《ストイケイア》第5巻にもすでに述べられているが,それを完成したのも19世紀の数学者K.ワイヤーシュトラス,R.デデキント,G.カントルらの業績であった。実数論は,彼らによって自然数論に帰着されたが,デデキントやG.ペアノは,集合と写像の考えを用いて自然数論を公理的に構成した。集合一般はカントルによって初めて考察の対象とされたが,それをあまり素朴に扱うと逆理が生じて矛盾の起こることが示され,E.ツェルメロやA.フレンケルはそれを避けるような公理を設け,それに基づいて集合論を展開した。
1900年パリで開かれた国際数学者会議で,ヒルベルトは今世紀の研究の対象となるべき23の数学の問題を挙げたが,その一つは算術(すなわち自然数論)の無矛盾を示すことであった。彼は数学基礎論を創始し,集合論に始まる全数学の無矛盾を示すことを目標とした。それは今日も十分満足すべき解決に到達してはいないが,それに関連してこの分野はいろいろの方向に進展した。
ガウスが18世紀と19世紀の境界に立っていたように,ヒルベルトは19世紀と20世紀をわかつ数学者である。本項目では数学の性格をはっきりさせることを急いだため,19世紀の多くの数学者の事績に触れないまま20世紀の初頭に話が進んでしまった。時代が進むとともに数学の進歩には加速度が加わり,1950年ころから今日まで30年ほどの間になされた数学の論文の量は,ギリシア時代から1950年くらいまでに発表された数学の業績の全量にも匹敵するといわれる。したがって19世紀以降の記述は簡略にせざるをえないが,代数学,解析学関係のことをなお1~2補っておこう。
代数学では,16世紀のイタリアで四次までの代数方程式が四則と開方で解かれていたが,五次以上の場合に同様の解法を得るための多くの数学者の試みは徒労に帰した。N.H.アーベルは1826年その不可能なことを証明し,É.ガロアはこの問題と方程式の根の置換群との関連を見抜いて,いわゆる〈ガロアの理論〉を創始した。そのころから抽象代数学の最初の部門としての群論が登場することになる。それ以後の代数学は単に代数計算の技術ではなく,代数系すなわち簡単な公理で規定された算法をもつ集合の構造を研究する分野となる。群に続いて環,体などの代数系が研究の対象とされた。
解析学方面では,上述のような基礎概念の確立もこの時代の特徴的な成果であるが,18世紀以来の古典解析の進展もある。J.B.J.フーリエは熱伝導の理論に関連し,フーリエ級数を導入したが,どのような関数がその級数で表現されるかの問題は,関数概念についての深刻な反省を促した。これは応用数学上の問題から純粋数学の本質的な発展がもたらされた好例として挙げられる。古典的な問題としては楕円関数論がまず取り上げられ,19世紀末には1変数複素変数の解析関数論が完成することとなった。ガウスはその方面でも先覚者であり,アーベル,C.G.ヤコビ,コーシー,ワイヤーシュトラス,リーマンらの貢献が大きい。それを多変数の場合に拡張することは20世紀にもちこされた。多変数代数関数論の幾何学的表現と見られる代数幾何学は19世紀後半イタリアで盛んに研究されたが,厳密性には欠けていた。それを基礎づけることも20世紀の課題となった。微分方程式は17世紀以来応用数学の主役を占め,オイラーらはある種の偏微分方程式をも解いていたが,19世紀にはコーシーらにより偏微分方程式の場合も含めて解の存在などに関する一般論が扱われるようになった。後者についてのS.コワレフスカヤによる〈基本定理〉が発表されたのは1875年であった。
現代の数学
20世紀の初頭には,数学の性格はほぼ明らかとなり,その進展は加速度的となっていた。それ以後の叙述はいっそう概略にとどめなければならないが,ヒルベルトが1900年に提出した問題と彼の業績についてはここにいちべつしておこう。
ヒルベルトの問題のうちには,集合論の問題(いわゆる連続体問題)や上述の数学基礎論の問題もある。物理学各部門の公理化というように漠然と述べられたものもあり,それらがどれだけ解決されているかについて明確に述べることはできない。しかしどの問題も数学者の興味をひき熱心に研究された。その約半数はすでに解決され,そのたびに学界の話題となった。その解決に日本の数学者が直接,間接に寄与しているものも少なくない。とくに数論に関するもの二つは高木貞治の提唱した類体論によって解決された(1920)。
ヒルベルトは代数学の不変式論の研究から出発し,幾何学基礎論,ついで数論,積分方程式論,ポテンシャル論などの研究に移り,晩年は数学基礎論に専念した。積分方程式論に関連してはいわゆるヒルベルト空間論を創始した。それはユークリッド空間を無限次元に拡張したもので,解析学の各方面に応用される。
1920年代のヨーロッパは二つの戦争の間にあり政治的には不安定であったが,ワイマール政府の下のドイツのゲッティンゲン大学には,ヒルベルトとともにE.ネーターが活躍し,抽象代数学の研究の中心となった。同じころポーランドにはS.バナッハらがいて位相数学(トポロジー)が盛んに研究された。バナッハはヒルベルト空間の拡張であるバナッハ空間の線形作用素論を解析の諸問題に応用した。位相数学と代数学とを用いて解析学を研究する方法を,そのころ日本では〈位相解析〉と呼んだが,その後世界的に行われている用語に合わせて〈関数解析〉と呼ぶようになった。
1930年代からフランスの数学者グループであるブールバキが《数学原論》を著し始めた。集合論から始め,代数学と位相数学にもとづいて,全数学を公理的に記述しようとするもので,いわばユークリッドの《ストイケイア》の現代版である。それは今日も完成してはいないが,基礎的部分は一応でき上がり,現在の数学の叙述形式はほぼそのスタイルに統一されている。今日の数学はその方法によって,18~19世紀以来残されている古典的問題や新たに生じてきた問題に取り組み,新しい分野の開拓に進みつつある。
20世紀後半における発展のとくに著しいのは多様体の研究である。1913年H.ワイルはリーマン面の研究で一次元複素解析多様体を厳密に定義したが,それに端を発して,微分構造,解析構造などをもつ多次元の実多様体あるいは複素多様体が定義され,豊富な内容をもつ理論が展開された。その立場から微分幾何学,リー群論,微分形式の理論が書きかえられ,この分野は長足の進歩をとげつつある。これに伴って微分方程式論,力学系の理論,微分幾何学の相互の連係も深まってきている。
関数解析も20世紀前半には主として線形問題を対象としていたが,今日では非線形問題の研究が盛んであり,変分法や確率論もその枠組に入れられている。L.シュワルツや佐藤幹夫による関数概念の拡張も著しい影響を及ぼした。また,それとはまったく異なる数学基礎論上の立場からであるが,A.ロビンソンは実数概念を拡張して極限操作によらないで解析学を展開しうることを示したのも注目をひいた。その方法による解析は,日本では超準解析と呼ばれている。
18世紀までは数学と自然科学などの関係に触れたが,19世紀以降は純粋数学の性格を明らかにするのを主眼としたため,他分野との関連が希薄になった。それを以下に補っておく。数学の分野は公理として明示された前提から厳密な論理で構成された体系であり,第1に無矛盾でなければならないことは前述のとおりである。だがその研究が学界の興味を喚起し進展していくためには,公理系が無矛盾であるだけでなく,その体系の展開がある審美的鑑賞に値し,その成果が何らかの意味で有用であることが期待されよう。ユークリッド幾何学,複素変数の解析関数論,あるいは群論などいずれもこの期待にこたえるものであった。〈有用〉とは必ずしも実用上の意味ではないが,フーリエ級数論のように他の分野への応用を意識してつくられた理論が純粋理論を刺激して意想外の発展をすることもあり,純粋に美しい体系として構想されたものが,後に重要な応用を見いだすこともある。円錐曲線論がケプラーに用いられたことを前に挙げたが,リーマン幾何学やヒルベルト空間論がそれぞれ一般相対論や量子論の記述に用いられたのは,20世紀になってからの事例である。
純粋な論理体系としての数学理論は,内容として何を盛ってもよいため,応用可能の範囲はいっそう広くなった。抽象代数学の群論や体論は実験計画の設計に用いられる。確率論は統計学と結びついて推計学を発展させ,品質管理にも応用される。コンピューターのソフトウェアの設計には数学基礎論の手法が用いられている。自然科学のみならず,人文・社会科学との関連も,20世紀の数学はますます広く深くなっている。他の諸科学と同様,数学も専門化が進んでいるのは事実であるが,社会との連帯は深層において強まっており,今後もいっそう強まるものと思われる。
執筆者:弥永 昌吉+伊藤 清
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「数学」の意味・わかりやすい解説
数学
すうがく
mathematics
数学は、物を数えたり、測ったりすることに始まる、数・量・図形などに関する学問である。われわれは日常、数学となんらかのかかわりをもちながら生活している。今日のように、経済組織、科学技術の高度に発達した国家・社会では、家計簿、銀行通帳など日常生活に直接かかわる部分から人工衛星の軌道計算に至るまで、数学は広がりと深みにおいてその影響力をいっそう増してきている。
歴史的には、土地測量や商業や金銭取引、航海や暦の計算、教会や宮殿の建設など、実用上の必要から用いられ発展してきた数学は、一方では自然現象の法則性を解明するための基本的方法およびその強力な手段を提供してきたが、その理論が実用に結び付くことをつねに意識して研究されてきたわけではない。むしろ数学に内在している論理に対する純粋に知的な好奇心からの研究が、往々にして独創的な理論を生み出してきた例が多い。これは数学が、芸術にも似た創作的な分野であることによる。つまり、人間精神の一つの表現としての数学は、論理的厳密さ・簡潔さへの志向性と美的完成への願望が反映されているものであり、その基本的要素は、論理と直観、解析と構成、一般性と個別性からなる。これらの対抗する力の相互作用およびそれらの統一への苦闘が、数理科学としての生命力や有用性を生み出しているのである。
[野口 廣]
数学の扱う対象
数学は、数学をそれ自身として研究する純粋数学と、力学・物理学など、他分野の科学からの要求に応じて数学を研究する応用数学に分類される。純粋数学に含まれる部門は、数学基礎論、数理論理学、集合論、代数学、群論、整数論、幾何学、微分幾何学、代数幾何学、トポロジー(位相幾何学)、解析学、複素関数論、関数解析学、関数方程式論、特殊関数、数値解析および確率論などである。応用数学は、グラフ理論、組合せ理論、統計数学、計画数学など、力学・理論物理学からの応用を目ざす数学が含まれる。数学教育の立場からみたときの数学は、幼児数学、初等数学(算数)、中学校数学、高等学校数学(代数、幾何、微積分など)、大学教養数学(線形代数、解析学など)および専門数学に分類され、専門数学は前述の純粋数学および応用数学を含めていう。今日の数学の扱う対象は、前記のように分類することができるが、その内容と力点の置き方が時代とともに大きく変化してきたのはいうまでもない。
たとえば、図形のとらえ方についてみてみよう。古代エジプトやバビロニアでは、古くから図形に関するかなりの知識をもっていた。それを幾何学として、理論的体系をもつ学問に発展させていったのはギリシア人である。ギリシア人たちは、三角形、四角形などの多角形や円周などの単純な図形の長さ、角、面積をさまざまに研究した。ピタゴラス(前500ころ)は、すでにバビロニア人たちに知られていた直角三角形の性質を、三平方の定理(ピタゴラスの定理)として確立し、その証明を与えた。また、ユークリッド(前300ころ)の『ストイケイア』(『幾何学原本』または『原本』)は、定義と五つの公理を基に厳密な推論を積み上げる方法をとり、幾何学は純粋な演繹(えんえき)体系の学問として確立されるに至った。この時代をやや下って、アルキメデス(前250ころ)やアポロニオス(前230ころ)は、平面における円、楕円(だえん)、放物線と立体、円柱や直円錐(えんすい)へとその研究対象を多様化させたが、力点を置かれていたのは、依然としてそれらの図形の面積・体積の計算であった。こうして、日常生活に必要な図形的研究のほとんどは、このギリシアの時代に完了したといえるほど深められていた。
他方、プラトン的精神は、幾何学において作図用の道具として許されるものが、定規とコンパスのみであるとするような厳格な規則を要求した。たとえば、次のギリシアの三大作図問題がそれである。「定規とコンパスのみを用いて(1)任意の角を3等分せよ。(2)与えられた立方体の体積の2倍の体積をもつ立方体を作図せよ。(3)与えられた円と等面積の正方形を作図せよ」。ギリシアの数学者たちの興味をひいたこの問題を解くために多くの数学者たちが挑戦したが、その試みはすべて失敗し、やっと19世紀に入ってから、この三つの問題の作図不能性が、幾何学的考察によってではなく代数的考察によって証明されることになる。
芸術が数学に影響を与えた例として特筆されなければならないのは、15~16世紀ルネサンス期の絵画・建築と幾何学の関係である。イタリアのレオナルド・ダ・ビンチや、ドイツの画家デューラーによって用いられた遠近法(透視画法)の手法を取り入れて、フランスのデザルグやパスカルは射影幾何学を創始した(17世紀)。射影幾何学は、射影と切断で不変な図形の性質を研究しようとするもので、ユークリッド幾何学と趣(おもむき)を異にする。ユークリッド幾何学においては、図形は完全なものとして与えられており、そのあるがままの性質を研究することが大きな意味をもっていた。したがって、ユークリッド幾何学では図形を変える性質の研究は視野には入っていなかったのである。ところが、射影幾何学では逆に、線分の長さ、角、平行などの概念は意味をもたない。
19世紀に入って、同じようにユークリッドの平行線公理の否定のうえにたちながらも矛盾のない体系をもつ非ユークリッド幾何学が発見・創始される。また、たかだか二次曲線の範囲にとどまっていた図形の研究は、ニュートン、ライプニッツによる微積分法の確立を経て、空間の中の滑らかな曲線や曲面としての図形を扱う微分幾何学へと発展する。
他方、18世紀のドイツの数学者オイラーの先駆的研究によって新たな光を与えられた図形は、「位相」という概念を通して研究されるようになる。そして、20世紀、図形は集合に位相を与えたものとして一般化され、あらゆる数学的対象は位相空間として把握されるに至った。現在、位相幾何学ともよばれるトポロジーによって、図形の位相的に不変な性質の研究がなされているが、これは、ギリシアの時代から遠く隔たった現代数学の、さらに一般性と抽象性を付け加えた形での図形の研究といえよう。
[野口 廣]
数学と他の学問との関係
中学校数学では数の四則演算と初等ユークリッド幾何学を教えるが、これらは、日用諸算としてわれわれの日常生活になくてはならない道具となっている。他方、高等学校以上の数学で教える二次方程式の解(かい)の公式などを考えてみればわかるように、数学とわれわれの日常生活との直接的関係はあまりないともいえる。こうしてみると、数学という学問の全体が目ざしているものと、われわれとは無縁のようにも思えるかもしれない。ここでは、数学と他の学問との密接不可分な関係をみることによって、間接的にではあるが数学と人間の関係のありようをみてみよう。
ユークリッドの『原本』は、のちに、その第五公理(平行線公理)を別の公理に置き換えた非ユークリッド幾何学が可能であることが発見されたにしろ、それは、純粋な演繹を通じて壮大な体系を築き上げるという学問の典型を提示した。ユークリッドの美しい幾何学の体系のなかには、定義と公理を前提とする論理だけで組み立てていこうとする現代数学の精神がすでに宿っていたのである。この事実は、ヨーロッパ思想に長らく影響を与え続けたギリシアの哲学者プラトンのことば、「幾何学は測地術にあらずして神性への第一歩である」によく示されている。数学はまず、哲学を含む諸学のあるべき姿をわれわれに示したのである。
ヨーロッパにおける近代数学は、商業資本に奉仕する商業算術から出発し、16世紀カルダーノやフェッラーリの代数学、17世紀デカルトの解析幾何学、ニュートンやライプニッツの微積分法などによって、古代・中世の古い殻を脱ぎ捨てて近代の衣をつけていった。カルダーノやフェッラーリは、三次および四次の方程式の根を求める努力を続けたが、その時代において、三次・四次方程式の根を求めなければならない差し迫った必要性は特別考えられない。したがって、彼らの研究は、純粋に知的興味あるいは遊戯的興味から発したものと考えられる。数学はこのように、遊戯ないし娯楽の対象として人間に関係してくる面もあるのである。
近世哲学の父といわれるフランスのデカルトは、その著『方法序説』のなかで、数学だけはいろいろな学問のうち、もっとも明白な真理を示すと認められる、という意味のことばを述べている。若いころから自然研究に数学を用いた彼は、数学的自然の研究を深め、この自然観に基づく全自然学の改革とこれを支える哲学の確立とに努めた。幾何学的図形を座標によって示す解析幾何学の方法は、デカルト哲学にふさわしいものであり、これはやがて微積分法を生み出す要素になっている。数学はデカルト哲学、広く近世哲学にとって不可欠なものであった。
また、ドイツの哲学者であり、今日使われている微積分の記号を導入したライプニッツは、その論文「結合法の理論」を、「すべての理論的真理をある種の計算に還元する一般的方法」とよんだが、これは今日の記号論理学の先駆ともみられるもので、ライプニッツの生涯の思想を方向づけたものである。このときから論理学は数学の一分野へ変わり始めたといえる。
また、17世紀、ガリレイによって地上の機械学として基礎づけられた力学は、ケプラーによる天体の力学的研究に発展し、さらにニュートンによって、地上と天上の物体の運動を統一して記述する、より普遍的な力学法則として確立される。こうして、古典力学の完成をみるに至るが、その際の数学の果たした役割は見逃すことができない。この時代、数学は自然科学の単なる末端的な道具ではなく、理論科学に基本的方法を示す学問として、かつ、それを支える不可欠の基盤であることが示された。
18世紀、オイラー、ラグランジュ、ラプラスらの数学解析は、周知のように今日の応用数学の礎石を形成した。つまり、ニュートンによって確立された力学的自然観のもとで、力学や天文学と結び付いた微積分学は解析力学として発展し、天文学、物理学、工学に奉仕する応用数学となってイギリス産業革命の時代の数学の主流を占めたのである。その応用範囲も、たとえばオイラーは船の運動から月の運動表の作成に至るまで、さらに耳の生理学の研究までも行った。
19世紀前半のドイツには、代数学、解析学、幾何学の各方面に大きく貢献した大数学者ガウスがいた。彼は、ゲッティンゲン大学在学中の19歳のとき、円に内接する正十七角形の作図に成功し、「このような円分理論における整数論的法則は天文学上のいかなる法則にも劣らず美しい」と歓喜している。このことばは、古代ギリシアにおける数学の研究によって人間の魂を善のイデアにまで高めたプラトンのことばに匹敵し、数学における審美精神の復興を告げるものであり、この精神が19世紀の純粋数学の大発展をもたらしたのである。
なお、19世紀なかばから、気体分子の運動などミクロの物質の運動を記述する物理学の分野として、統計力学、量子力学が発展していくが、これを基礎づける数学理論としてパスカルのころから始まった確率論も重要な役割を果たしている。
[野口 廣]
数学の方法
数学における方法は、いろいろに分類することができるが、ここではその代表的な方法について述べる。
第一の方法は公理的方法である。公理的方法とは、対象を徹底的に分析したうえで、ある公理を定立し、その公理によって総合していく立場である。ユークリッドにおける演繹の手法は、ピタゴラスの影響のもとに形成されたもので、ユークリッドはまず、すべての図形を分解した。そして、それを三角形にまで分解し、さらに、その三角形を頂点、辺、角などに分解したうえで、点、直線、平面と角の基本概念を論じ、これと現実とのかかわり、たとえば直線は幅のない長さである……、と述べていくが、これは定義の形をとってはいるものの、その性質を公理で規定する無定義概念である。そして、その次にこれらの基本概念間の関連が仮定として述べられていくが、これが公理ともいえるものである。このようにして、たとえばピタゴラスの定理のような諸定理が、一つの総合としてこの公理から論理的に導かれていくのである。
ところが、長い間、だれもが信じて疑わなかったユークリッドの平行線の公理を否定した非ユークリッド幾何学の新たな展開は、数学者たちに公理の性格について反省する機会をもたらし、公理は理論の前提としての仮定であるという意味に解されるようになった。これを公理の性格として掲げ、それに基づいて理論を展開するのが数学であるとしたヒルベルトは、この思想によってユークリッド幾何学を再編成した。つまり、数学的対象(点、線、数など)はそれ自体がア・プリオリな意味をもつのではなく、それらの意味づけは、それらの相互関係を規定する命題(公理)によってのみ与えられるとしたのである。こうした彼の仕事によって数学基礎論および数理論理学は、確固とした土台を与えられ、形式公理的手法が確立していったのである。
第二の方法は発生的手法である。幾何学が早くから公理的に扱われたのに対して、数についての理論は、物と物との対応を自明に語るものとして自然に生成され、それに関する定理も、このすでに確かめられた数の性質や数と数との関係を整理して述べるという段階に長い間とどまってきた。たとえば自然数はわれわれが扱う数のなかでもっとも簡単なものであり、物の個数を数えたり、順序をつけたりするのに用いられる。これに対して、一つの正方形の対角線の長さの表すような数があり、これは整数でも分数でも表すことはできない。このような無理数の存在は、ギリシアのピタゴラス学派の数学者を驚かせ、大きな衝撃を与えた。自然数や無理数をすべて含む数である実数の公理的定義や、それに基づく解析学の体系の構築はたいへんに遅れ、ペアノの公理系によって、自然数の集合Nが確立され、その元を自然数と名づけるようになったのは、やっと19世紀に入ってからのことである。
発生的手法に基づく理論化は、カントルによるパラドックス、「Sはすべての集合の集合である」などを生じ、20世紀に入って、数学とは何かという論議が改めて熱心に交わされた。カントルのパラドックスは「集合論について」の論文において提起されたもので、これは、「すべてのクレタ人はうそつきである」というクレタ人のことばが真であるか偽であるかという4~6世紀のパラドックス(エピメニデスのパラドックス)と同様の問題を含んでいる。パラドックスの生じる原因は、集合という概念を無制限に拡大して用いた点に求められる。この矛盾克服について、主として数学基礎論の立場から、論理主義、直観主義および形式主義による接近が試みられている。
第三に数学の方法としてあげられるのは、一般化と抽象化である。この傾向は現代数学において著しい。たとえば、一次元、二次元の図形である線分や円板で成り立つ連続写像の不動点定理がみいだされると、これを三次元、四次元、……、そして一般にn次元のある種の図形についても成り立つというブローエルの不動点定理をみいだそうとする。このとき、一次元、二次元の定理はこの一般的定理の特別な場合となる。これが一般化の考えである。この考えは場合によっては有限なnの場合を越えて、角谷(かくたに)の不動点定理のように無限次元の場合にも一般化される。そして、普通、一般化は可能な限り追求される。
数は、たとえば加法について閉じた体系となっているが、この数の演算についての性質を抽象化(公理化)したものが群である。また、直線、平面、空間という図形は、n次元ベクトル空間へと一般化されると同時に抽象化される。抽象化によって無数のそれぞれの場合の異なる結果がただ一つの定理によって示しうるようになる。
こうした一般化と抽象化は、とくに現代の抽象数学において顕著である。ブルバキとよばれる数学者グループの手になる現代数学の基礎に関する百科全書的な膨大な著述は一般化と抽象化の金字塔である。ブルバキの構成員であるA・ベーユは、「数学とは人間精神の名誉のためにあるものである」と述べている。
20世紀の数学は、ガウスによる審美精神の復興の動きと相まって抽象化と一般化の運動が展開され、その前半においては数学固有の活動が広範囲にわたって活発に行われてきた。第二次世界大戦後は、戦時中の数学者の実際的経験に刺激されて、ウィーナーによるサイバネティックス、ノイマンによるゲームの理論、そしてコンピュータの発明によっておこってきたコンピュータ・サイエンスと数学との間に新しい学問をつくり始めている。これらの新しい科学は現在では数理科学とよばれており、この数理科学を通して数学の現代社会に対する関係も大きく変貌(へんぼう)しつつある。
[野口 廣]
数学における論理性の点検
以上、大ざっぱに数学における方法について述べてきたが、ここで公理的方法および発生的手法のいずれもが到達した数学基礎論について簡単にみてみよう。論理主義とは、数学を論理学の一分野であるとみなす説で、主としてイギリスの哲学者バートランド・ラッセルによって唱えられた。古くはライプニッツが、論理学こそ他のすべての基礎となる万有科学であるとした(1666)のに始まる。論理学はデーデキントやフレーゲにより論理の算法としてつくられ、ラッセルは「数学のすべては論理学へと還元される」と述べている。ラッセルはホワイトヘッドと協力して、記号を用いた『プリンキピア・マテマティカ』(『数学原理』)を論理学の一部としてまとめているが、この著書を評してワイルは、「数学はもはや論理のうえにではなく、論理主義者たちのある種の楽園のうえに築かれている」と述べている。
直観主義は、数学的真理や対象が、数学を考えていく意味や内容によって直接にとらえられるものであるという考えにたつ説で、この立場をとる数学者にクロネッカーやポアンカレがいる。無理数を有理数の無限列によって定義し、その無理数の概念に基づいて数学解析を行おうと試みたワイアシュトラースに対して、クロネッカーは整数の直観を重視した。そして、有限的に構成されるもののみの存在を主張したので、直観主義の先駆者とみられている。数学を根本から直観主義的に再構成しようとしたのはブローエルLuitzen Egbertus Jan Brouwer(1881―1966)である。彼はアリストテレス以来の古典的論理の法則に批判を投げかけた。とくに、「AかAでないかのどちらかである」という排中律の無制限の使用は不当であると主張、これは、Aか、Aでないかのどちらか一方が正しいことがわかったときにのみ正しいと主張した。したがって、ブローエルは帰謬(きびゅう)法による間接的証明を認めない。また、数学では無限という概念が重要な役割を果たすが、彼の立場では数列0、1、2、……のみが無限へ接近するための唯一可能な開かれた窓となっている。こうして、古典的算術は直観主義に見合うが、古典的解析学はすべてこの主義の批判の対象となる。ブローエルは、直観主義的な解析学と集合論を築いた(1918~24)が、あまりにも複雑で従来のものと異なりすぎていて、とても応用の効かない体系であった。
形式主義は公理主義ともいう。直観主義の認める範囲を超えて、これまでにつくられてきた古典的数学のある部分をそのまま認めたうえで、徹底的に形式化された数学の公理系の無矛盾性を証明することによって問題を解決しようとするヒルベルトのプログラムをいい、この考えは前述のように数学基礎論の道へと続いている。
[野口 廣]
『クーラント、ロビンズ著、森口繁一訳『数学とは何か』(1966・岩波書店)』▽『村田全・茂木勇著『数学の思想』(1966・日本放送出版協会)』▽『ソーヤー著、芹沢正三訳『現代数学への小道』(1968・岩波書店)』▽『ソーヤー著、宮本敏雄・田中勇訳『数学へのプレリュード』(1978・みすず書房)』▽『『数学と文化』(『遠山啓著作集 数学論シリーズ6』1980・太郎次郎社)』▽『飯高茂他編、小川束・平野葉一著『数学の歴史』(『講座数学の考え方24』2003・朝倉書店)』▽『山本芳彦著『数論入門』(2003・岩波書店)』▽『M・クライン著、中山茂訳『数学の文化史』上下(1977・社会思想社・現代教養文庫)』
百科事典マイペディア 「数学」の意味・わかりやすい解説
数学【すうがく】
→関連項目位相幾何学|関数論|算数
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「数学」の意味・わかりやすい解説
数学
すうがく
mathematics
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
普及版 字通 「数学」の読み・字形・画数・意味
【数学】すうがく
字通「数」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
世界大百科事典(旧版)内の数学の言及
【日本数学会】より
…1946年設立の数学者の全国組織。1945年12月日本数学物理学会の理事会で,日本数学会と日本物理学会との二つの学会に分離することが決定され,数学では弥永昌吉が中心となり,46年4月第1回の年会が開かれた。…
※「数学」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
目次 飼養文化 北アメリカ 北方ユーラシア偶蹄目シカ科の哺乳類。北アメリカでは野生種はカリブーcaribouと呼ばれる。角が雄だけでなく雌にもふつうある。体長130~220cm,尾長7~20cm,...