曲面（読み）きょくめん

精選版 日本国語大辞典

きょく‐めん【曲面】

〘名〙

① 面のうち平面でないもの。球の表面や円柱、円錐の側面など。

※ガトフ・フセグダア（1928）〈岩藤雪夫〉四「此の太平洋を三股位に跨いでゐるかも知れない程の潮の曲面とその頂点(てっぺん)が一筋か二筋、見えるだけだ」

② 正方形から空間への連続写像。また、それによる正方形の像。

③ 正方形の位相写像による像をある条件に従ってつなぎ合わせたもの。

出典　精選版 日本国語大辞典

デジタル大辞泉

きょく‐めん【曲面】

曲線が動いてできる面。連続的に曲がった、平面でない面。数学では、平面の一部分の三次元空間への連続写像。
[類語]面・平面・表面・球面・断面・側面・底面・半面・片面・両面

出典　小学館

日本大百科全書(ニッポニカ)

曲面
きょくめん

解析学の立場からは、球面、円柱、円錐(えんすい)、二次曲面、螺線(らせん)面などのように、空間内でその点の座標が二つの実変数u、vの連続関数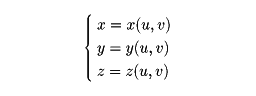

として与えられているものが曲面である。曲面はまた、
　F(x,y,z)=0　(1)
のように陰関数の形で与えられることもある。あるいは、
　z=f(x,y)　　(2)
の形で与えられることも多い。(1)が(2)のようにどれかの変数について解いた形にできるためには、偏導関数F_x、F_y、F_zのどれかが0でなければよい。このような点は正則点とよばれるが、非正則点においては、曲線の場合の特異点のように、その近くで曲面は複雑な様相を示す。曲面上の1点P(a,b,c)において、Pの近くにとった曲面上の点P₁、P₂とPの3点によって決まる平面で、P₁、P₂をPに近づけた極限の平面をPにおける接平面という。その方程式は、
　F_x(x-a)+F_y(y-b)+F_z(z-c)=0
あるいは、
　z-c=f_x(x-a)+f_y(y-b)
などで表される。

［竹之内脩］

曲面積

曲面の面積、すなわち曲面積は、曲面を細かに分割してできる各小部分の面積の総和として与えられる。各小部分の面積は、その中の1点における接平面への正射影の面積で近似して測る。これを表す式は、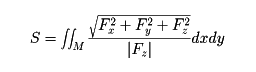

あるいは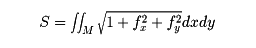

などの形になる。

［竹之内脩］

　トポロジーの立場からいえば、平面、球面、また三角形などは、すべて曲面とよばれる位相空間となる。曲面はまず、平面や無限に長い円柱面などのように無限に伸びるもの、すなわちコンパクトでないものと、球面や円板などのように、コンパクトなものに分けられる（コンパクトは、有界な閉集合のこと）。そしてコンパクトな曲面のうち、円板はその円周が境界となっているし、円板に一つ穴をあけた円環面は内外の円周がその境界となっている。これに反して球面や輪環面（トーラス）は境界のない曲面であり、閉曲面という。

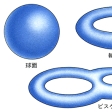
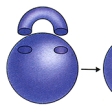
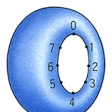
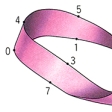
　閉曲面としては、まず球面や輪環面や二つの穴あきのビスケット曲面などがある（図A）。輪環面は、球面に二つの円板の穴をあけ、これに円柱の上下の円周を貼(は)り付けたものである。すなわち球面に一つのハンドルを取り付けた曲面とみられる（図B）。同様に二つの穴あきのビスケット曲面は、球面に二つのハンドルを取り付けたものである。このようにして球面にn個のハンドルを取り付けた、n個の穴あきの曲面ができる。こうしてできる曲面は可符号閉曲面とよばれる。これに反して、球面に一つの円板の穴をあけ、これにメビウスの帯の境界の円周を貼り付けると、射影平面とよばれる曲面ができる（図C）。一般に球面にn個の円板の穴をあけて、それぞれにn個のメビウスの帯（図D）の境界を貼り付けてできる閉曲面を不可符号の閉曲面という。

　任意の閉曲面は、前記のように構成される閉曲面のいずれか一つと同位相であり、貼り付けるハンドルまたはメビウスの帯の個数が異なるものは互いに同位相とはならない（閉曲面の位相幾何の基本定理）。不可符号の閉曲面は、メビウスの帯と同じように、適当な道に沿って小円板を動かすと、1周したあとに円板の向きが逆転するという性質をもっている。また、不可符号の閉曲面はけっして三次元空間へ自分自身と交わることなく入ることはできない。

［野口　廣］

[参照項目] | メビウスの帯

曲面（球面、輪環面、ビスケット曲面）〔…

曲面（輪環面）〔図B〕

曲面（射影平面）〔図C〕

曲面（メビウスの帯）〔図D〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

曲面
きょくめん
surface

直観的には，球面や円柱面のような2次元の点集合が，3次元空間の曲面である。これを，直交座標系O- xyz における方程式によって表示すれば，f(x，y，z)＝0，z＝F(x，y) ，あるいは媒介変数 u，v を用いて x＝x(u，v)，y＝y(u，v)，z＝z(u，v) と表わされる。たとえば，中心の座標が (a，b，c) ，半径が r の球面の方程式は，球面上の任意の点の座標を (x，y，z) とすると
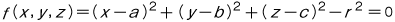で表わされ，また媒介変数を u，v として，これを球座標で表示すれば
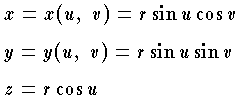となる。この u，v を曲面上の曲線座標という。一般に，関数 f(x，y，z) が x，y，z に関して微分可能であって，その各点における偏導関数が同時にすべて0にならないとき，f(x，y，z)＝0 を満足する点集合はなめらかな曲面といわれる。関数が媒介変数 u，v によって表示されているときは，関数 x＝x(u，v)，y＝y(u，v)，z＝z(u，v) が u，v に関して微分可能であるとき，これをなめらかな曲面という。曲面を数学的に厳密に取扱うためには，抽象的な曲面，すなわち3次元ユークリッド空間内の2次元の多様体を考え，これを曲面と定義する。こうすると，曲面の位相的研究が可能になる。たとえば，コンパクトな曲面 (閉曲面──球や輪環体) の類別およびコンパクトでない曲面 (開曲面) の位相的性質の研究が可能である。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典 第２版

きょくめん【曲面 surface】

曲面は曲線が空間内を動いたときにできる図形と考えられる。したがって，空間内の曲線とは一つの媒介変数tを用いてx＝f(t)，y＝g(t)，z＝h(t)と表される座標(x,y,z)をもつ点全体のつくる図形であると定義するのと同様に，曲面とは，二つの媒介変数u,vを用いてx＝f(u,v)，y＝g(u,v)，z＝h(u,v)と表される座標(x,y,z)をもつ点全体のつくる図形である，と定義する。この定義式からu,vを消去すればF(x,y,z)＝0のような方程式が得られ，これは曲面上の点の座標の満たす関係式となる。

出典　株式会社平凡社

百科事典マイペディア

曲面【きょくめん】

曲線が空間内を連続的に運動してつくられる図形。狭義には面を平面と曲面に分け，平面でないものを曲面という。一般には円の内部と同位相（位相幾何学）な集合またはその和集合（集合）と定義される。境界のない曲面を閉曲面といい，自分自身を切らない曲面を単一曲面という。→二次曲面／曲線

出典　株式会社平凡社