精選版 日本国語大辞典 「次元解析」の意味・読み・例文・類語
日本大百科全書(ニッポニカ) 「次元解析」の意味・わかりやすい解説
次元解析
じげんかいせき
物理法則を表す等式は、物理量の単位の選び方によらず成り立つはずである。そのためには、その両辺は同じ次元をもたなければならない。この事実に基づく解析を次元解析という。
物理量は(簡単に説明するため電磁気的なものを別にすれば)すべて長さ、質量、時間の組合せで定義される。それぞれを[L]、[M]、[T]で表すと、たとえば速度は変位(つまり長さ)を時間で割って定義されるため、その次元は
[速度]=[LT-1]
と書き表すことができる。加速度は速度の変化を時間で割って定義するため
[加速度]=[LT-2]
そして力はニュートンの運動の法則により質量と加速度の積に等しいため
[力]=[MLT-2]
である。基本量からの組み立てを表す先のような式を次元式という。単なる数や、物の個数、あるいは
[質量の比]
=[M][M]-1
=[M0]
のような比は無次元であるという。
次元式のなかにTがγ乗で含まれている物理量は、時間の単位をr倍にすると、その大きさを表す数値が1/rγ倍になる。他の基本量についても同様であるため、物理法則を表す式は、その両辺の物理量が同じ次元式をもつものでなければならない。このことから法則の推定ができる場合もある。たとえば、質量m、長さlの単振り子の周期は、これに重力加速度gを加えて
(周期)=mαlβgγ×(無次元の定数)
の形にすることができると予想される。
[右辺]=[M]α[L]β[LT-2]γ=[MαLβ+γT-2γ]
これが[左辺]=[T]と同じになるのは
α=0, β+γ=0, -2γ=1
のときである。よって、γ=-1/2, β=1/2となり、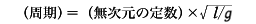
で表されることがわかる。次元解析では無次元の定数までは定められない。力学によれば、この場合の定数は2πである。電磁気的な量を組み立てるには普通、電流の次元[I]を加える。同時に真空の誘電率として次元をもつ定数ε0を導入するので、その次元解析には注意を必要とする。
[ε0]=[L-3M-1T4I2]
である。次元解析は相似法則の発見や模型実験の設計にも有用である。
[江沢 洋]
改訂新版 世界大百科事典 「次元解析」の意味・わかりやすい解説
次元解析 (じげんかいせき)
dimentional analysis
複雑な現象に関し,関係する諸量の間に成り立つ物理法則を見いだそうとする場合に用いられる手法。次元解析は〈物理法則は必ず無次元数の間の関係として表される〉という定理にもとづいている。無次元数とは,物理量を組み合わせてつくった次元のない数である。物理量は一般に次元をもつが,無次元数はこれを掛けたり割ったりして組み合わせてつくられる。たとえば,流れに関係する現象では流速Uと管径dと密度ρと粘度μを組み合わせてρUd/μという量をつくると無次元になるが,これはレーノルズ数と呼ばれ,ふつうReと書かれる。
物理法則は無次元数の関係で表されるという定理に従うと,かりに関係する無次元数がA,Bと二つしかないとき,物理法則はA=f(B)という形で表されるはずである。ここでf(x)は一般的な関数を表す。たとえば,流れによる伝熱という現象では,伝熱係数hを含む無次元数は熱伝導率をkとしてhd/kとなる。これはヌッセルト数と呼ばれ,Nuと書かれる。この現象に関係する無次元数はほかにはレーノルズ数しかない。したがって伝熱法則は必ずNu=f(Re)の形で表されるはずである。法則の具体的な形を知るには,実験によってf(x)の形をきめてやりさえすればよい。この場合,流速を変えても,管径を変えても,レーノルズ数が同じなら,ヌッセルト数は同じになるはずで,流速と管径を独立に変えて実験を行う必要はない。これを保証してくれるのが次元解析である。
物理法則は無次元数の間の関係として表されるという定理は次のように証明される。物理学が数学と異なる点は,扱う量が次元をもっていることである。次元をもつ量では二つの量の次元が同じでなければ加算はできない。このことから次の重要な結論が導かれる。物理法則がy=f(x)と書ける場合,f(x)が一般の関数でよいためにはx,yは無次元でなければならない。なぜならf(x)が一般の関数ならテーラー展開の定理(テーラー級数)によりf(x)はxのべき乗の項の和として表されるはずだが,xが次元をもつ量だと,異なるべき乗の項を足し合わせることができないからである。ただし物理法則がaを次元をもたない定数としてy=axと線形に表される場合は,x,yともに次元をもつ量でもかまわない。しかしこのときはxとyの次元が等しいので,z=y÷xという新しい無次元数をつくると,この物理法則はz=a(aは定数)という形にやはり無次元式で表せる。オームの法則とか,ベルヌーイの定理とかいう簡単な物理法則はほとんどすべてこの場合にあたる。
執筆者:西村 肇
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「次元解析」の意味・わかりやすい解説
次元解析
じげんかいせき
dimensional analysis
 。 k や G(θ) は次元解析では知ることができず,物理方程式を正確に解くか,実験によって求めなければならない。一般に実験によって実験式を求めるとき,関係式がまったくわからないのに比べて,この程度でもわかっていれば,実験の手間が非常に省ける。複雑な系では特に効用が大きい。前述の方法を一般化したものにバッキンガムの π 定理がある。
。 k や G(θ) は次元解析では知ることができず,物理方程式を正確に解くか,実験によって求めなければならない。一般に実験によって実験式を求めるとき,関係式がまったくわからないのに比べて,この程度でもわかっていれば,実験の手間が非常に省ける。複雑な系では特に効用が大きい。前述の方法を一般化したものにバッキンガムの π 定理がある。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「次元解析」の意味・わかりやすい解説
次元解析【じげんかいせき】
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の次元解析の言及
【次元】より
…この特別な場合として,ある関係を表す方程式の両辺は同じ次元をもたなくてはならない。このことを用いて未知の関係を推定する場合があり,この推定法を次元解析と呼ぶ。【小野 健一】。…
※「次元解析」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
目次 飼養文化 北アメリカ 北方ユーラシア偶蹄目シカ科の哺乳類。北アメリカでは野生種はカリブーcaribouと呼ばれる。角が雄だけでなく雌にもふつうある。体長130~220cm,尾長7~20cm,...

