次元（読み）ジゲン（英語表記）dimension

デジタル大辞泉

じ‐げん【次元】

１ 数学で、一般的な空間の広がり方の度合いを表すもの。座標の数で表される。線は一次元、面は二次元、立体は三次元。空間は三次元であるが、n次元や無限次元も考えられる。
２ 物理量を長さ・時間・質量の積の形で表示したもの。
３ 物事を考えたり行ったりするときの立場。また、その程度や水準。「話の次元が低い」「それとこれとは次元の違う問題だ」
[類語]（3）観点・視点・視座・見地・目線・着眼点・目の付け所

出典　小学館

精選版 日本国語大辞典

じ‐げん【次元】

1. 〘 名詞 〙
2. ① 数学で、一般的な空間の広がりの度合を表わす数。直線は一次元、平面は二次元、通常の空間は三次元であるが、ｎ次元や無限次元の空間も考えられる。ディメンション。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕
3. ② 物理量の性質を表わすもの。また、その基本単位との関係。たとえば長さの次元をＬ、質量の次元をＭとすると、面積の次元はＬ²、密度の次元はＭ／Ｌ³である。ディメンション。
4. ③ ある物事を考えたり行なったりするときの立場。また、その程度。考え方や行為などの水準。
   1. [初出の実例]「『想世界』『内部生命』は実世界とはその次元を異にしたより高次の精神の世界であり」(出典：北村透谷論（1946）〈小田切秀雄〉三)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

次元 (じげん)
dimension

ディメンションともいう。

（1）数学における次元　常識的には，ユークリッドの《ストイケイア》にあるように，線とは幅のない長さ，面とは長さと幅をもつもの，立体とは長さと幅と高さをもつものとされ，また線の端は点，面の端は線，立体の端は面であるとされている。このような理由で，点を0次元，線を1次元，面を2次元，立体を3次元の図形と呼んでいる。このことは点の位置は解析的には線上では一つの実数で，面上では二つの実数の組で，立体内では三つの実数の組で表されることに対応している。このようにみるとき，次元とは図形上で点の位置を指定するのに必要な座標の個数といってよいようである。しかしながら，直線上の点と平面上の点との間には1対1対応がつくことや，正方形全体を埋めつくす連続曲線（ペアノ曲線）の存在することなどを考えると，上の定義は厳密とはいえない。ところで，線は点（0次元）で切断することによって二つの部分に分けられるが，面を二つの部分に分かつには点では不十分で線（1次元）で切断しなければならない。また，立体を二つに分かつには線では不十分で面（2次元）で切断しなければならない。次元のもつこの帰納的性質に着目して，点集合の次元が帰納法により次のように正確に定義される。まず空集合は－1次元であるとする。次に点集合Sが－1次元ではなくて，Sの各点に対し，それを囲む領域でその境界とSとの交わりが－1次元となるものがいくらでも小さくとれるとき，Sは0次元であるとする。さらに点集合Sが－1次元でも0次元でもなくて，Sの各点に対し，それを囲む領域でその境界とSとの交わりが0次元であるものがいくらでも小さくとれるとき，Sは1次元であるとする。以下これを続けて，点集合Sがn次元であるとは，Sはn－1次元以下ではなくて，Sの各点に対し，それを囲む領域でその境界とSの交わりがn－1次元であるものがいくらでも小さくとれるときであると定義する。現象空間における図形の次元は3以下であるが，数学で考える抽象空間（位相空間）では3より大きい次元をもつ点集合，さらには無限次元の点集合がいくらでも存在する。例えばn個の実数の組（x₁，x₂，……，x_n）を点とし，2点（x₁，x₂，……，x_n），（y₁，y₂，……，y_n）の間の距離が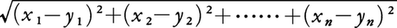，で与えられる空間の次元はnであり，この空間の中で条件x₁²＋x₂²＋……＋x_n²＝r²（rは正の定数）を満たす点（x₁，x₂，……，x_n）全体のつくる集合の次元はn－1である。また，ヒルベルト空間は無限次元である。
執筆者：中岡 稔（2）物理学における次元　ある量を数量的に表すには適当な単位を決める必要があるが，単位の決め方には尺貫法やヤード・ポンド法のように各種の量の単位を互いに無関係に決めるやり方と，メートル法のように必要最小限の基本単位から一定の約束に基づいて次々に他の単位を決めていくやり方とがある。前者をインコヒーレントな単位系，後者をコヒーレントな単位系と呼ぶ。コヒーレントな単位系では基本単位の選び方を変えると，それに応じて他の量の単位も変わり，したがってその単位で表す同じ量の数値が変わる。例えば，速さのコヒーレントな単位はCGS単位系ではcm/s，MKS単位系ではm/sであり，100cm/s＝1m/sとなる。その際，ある量の単位が基本単位のそれぞれの何乗に比例して変化するかをその量の次元と呼ぶ。例えば，上に例示した速さは，長さについて1次元，時間について－1次元，質量について0次元の量である。

　二つの量の積の次元はそれぞれの量の次元の和に等しい。二つの量を加えたり引いたりできるのは次元が一致する場合に限る。この特別な場合として，ある関係を表す方程式の両辺は同じ次元をもたなくてはならない。このことを用いて未知の関係を推定する場合があり，この推定法を次元解析と呼ぶ。
執筆者：小野 健一

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

次元
じげん
dimension

ディメンション、ジメンションともいう。空間内において、各点を指定するのに必要な座標の数をその空間の次元という。ユークリッドの『原本』（『ストイケイア』）では、「点とは部分をもたないものである。線とは幅のない長さである。面とは長さと幅のみをもつものである。立体とは長さと幅と高さをもつものである」と定義しているが、これが次元に関するもっとも素朴な観察であろう。長さ、幅、高さ（あるいは深さ）が次元であり、空間はこの三つの次元をもっている場所の集まりとギリシア時代には考えられていた。

　この考えはガリレオによって、さらに明確に次のように述べられている。「空間の1点を通り、互いに直角に交わる直線は三つあり、4本以上の直線を直角に交わらせることはできない。よって空間の次元は3である」。

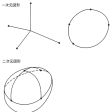
　このガリレオの説を述べた『天文対話』がローマ法王の忌避に触れていた1637年に、デカルトは『方法序説および三つの試論』を発表したが、この三つの試論の一つが「幾何学」である。これは今日の解析幾何学の誕生を示すものであるが、同時に次元を確定する座標軸が空間に設定されるというアイデアを与えている。すなわち、図Aのように、直線上の点の位置は、基点を一つ固定する（数0を対応させる）と、実数と対応し一つの座標軸で定まる。平面上の点は縦・横の二つの座標軸をとれば、二つの実数の組み(x₁, x₂)と対応する。そして空間の点は三つの座標軸によって、三つの実数の組み(x₁, x₂, x₃)で表される。よって直線は一次元、平面は二次元、空間は三次元の図形であると考えられる。すると、われわれの直観には訴えることはできないが、四つの実数の組み(x₁, x₂, x₃, x₄)の集合として四次元空間（x₁、x₂、x₃は普通の空間の次元で、x₄は時間軸であるとみて、四次元空間は物理学などでは時空間とよばれることもある）、五つの実数の組みの集合としての五次元空間、一般にn個の実数の組みの集合としてn次元空間が考えられる（1点は0次元空間とみなす）。こうした考えをさらに拡張して、今日では無限次元の空間もいろいろと考えられている。

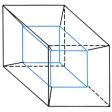
　線分や円周などの図形は直線と類似の図形であるので、これらの次元も一次元であるとみなすほうが自然である。そこで、図Bのような数え方で線分（1単体）を何個かその端点で接合してできる図形はすべて一次元図形であるという。この場合、線分はどのように曲がったものでもよいとする。同様に三角形（2単体）と線分とを組み合わせてできる図形は二次元図形である。ここで三角形はどのように曲がっていてもよいので、たとえば球面などは二次元図形である（図C）。一般にn次元以下の単体からなる多面体はn次元の図形である。図形の次元はその局所的なホモロジー群またはルベーグの敷石定理などを用いても定めることができる。われわれは三次元空間の中に生きているので、三次元空間以外の三次元図形や四次元図形などは三次元空間の中では描けないので、現物を示すことはできないが、平面の中に三次元図形の立方体を描くように、四次元の立方体を描いてみると図Dのようになる。

［野口　廣］

『田尾鶉三著『次元とはなにか』（講談社・ブルーバックス）』

[参照項目] | ホモロジー

直線、平面、空間の次元〔図A〕

線分と線分を接合してできる図形〔図B〕

一次元図形と二次元図形〔図C〕

四次元の立方体〔図D〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

次元
じげん
dimension

物理量 Q の大きさや形態は問題にせず，種類だけを指定するものを Q の次元，あるいはディメンションといい，[Q] で表わす。たとえば，振り子の周期，放射能の半減期，人の寿命などはすべて時間Tという種類の量であるから，[周期]＝[半減期]＝[寿命]＝T などと表わす。物理量の大きさを表わす数値は用いた単位の大きさに比例する。つまり物理量の大きさは単位に相対的であるが，同種の2つの物理量の大きさの比 (たとえば密度の比で与えられる比重) は用いた単位の大きさに関係しない。この事実を「相対的大きさの絶対的意義の原理」という。この原理から，物理量 Q が量 A ，B ，C ，… の関数ならば，Q は kA^αB^βC^γ… という形で必ず表わせることになる。 k は数係数，α，β，γ，… は0または正，負の整数または分数である。数係数 k は次元に関係がないので，Q の次元は [Q]＝[A^αB^βC^γ…] で与えられる。これを次元方程式といい，α，β，γ，… をそれぞれ A ，B ，C ，… に関する Q の次元という。したがって，適当に選んだ少数個の基本量の次元を組合せて，他の物理量の次元を導くことができる。力学量では長さL，質量M，時間Tを基本量に選ぶことが多く，たとえば速度 v ，力 F の次元はそれぞれ [v]＝LT^-1 ，[F]＝LMT^-2 となる。次元の考えは基本単位から組立単位をつくって単位系を構成するときの基礎をなす。電磁気量の次元を力学量の次元だけから組立てるのが静電単位系や電磁単位系の考え方であるが，次元に分数指数が入るので不便である。これに対し，電磁気量の基本量として電流を加えるのがMKSA単位系の考え方であって，電磁気量の次元が整数指数だけなので，計算に便利である。弧度法では，円の中心角 θ をつくる弧の長さを半径の長さで割った値で θ を表わすので，θ の次元は [θ]＝LL^-1＝L⁰ である。 LL^-1＝1 であるから [θ]＝[1] ，または L⁰ の指数0を用いて [θ]＝[0] と書き，角 θ は無次元であるという。 [密度]＝L^-3M であるが，水の密度との比で与えられる比重は [比重]＝[0]＝[1] と表わされる無次元量である。

次元
じげん
dimension

数学において，空間内の点を指定するのに必要な独立な座標の数。直線上の点は1つの実数で，平面上の点は2つの実数で，普通の空間内の点は3つの実数で指定され，それぞれ次元の数は1，2，3である。一般に n 次元空間や無限次元空間も考えられる。さらに位相空間にも次元を導入することができる。この位相空間の次元を研究する分野を次元論という。なお0次元は，一般に1点あるいは有限個の点から成る集合と考えてよい。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

次元(数学)【じげん】

点の位置は，線上では一つ，面上では二つ，空間内では三つの実数（座標）で表され，この意味で線・面・空間をそれぞれ１次元空間・２次元空間・３次元空間であるという。これを拡張して４次元，n次元，無限次元の空間が考えられる。またベクトル空間では，一次独立なn個のベクトルの組が存在し，n＋１個以上のベクトルの組はすべて一次従属であれば，次元はnであるという（ベクトル空間）。次元の概念はさらに距離空間や位相空間にも導入され，より厳密な定義を与えられている。→次元（物理）
→関連項目次元解析

次元(物理)【じげん】

ディメンションとも。ある物理量が長さL，時間T，質量Mなどの基本的な物理量とどのように関係するかを示す構造。たとえば加速度Aは［A］＝［LT(-/)²］の関係をもち，長さにつき１次元，時間につき−２次元である。→国際単位系
→関連項目次元（数学）

出典　株式会社平凡社

化学辞典 第2版

次元
ジゲン
dimension

【Ⅰ】空間を構成する独立なベクトル成分の数．一次元は直線，二次元は平面，三次元は立体である．【Ⅱ】物理量はそれぞれ基本単位の組合せでつくられる単位によって表される．とくに長さL，質量M，時間Tを使って[L^l M^m T^t]のように表されることがしばしばある．たとえば，速度[LT^－1]，力[MLT^－2]など．これらの表示を次元とよぶ．

出典　森北出版「化学辞典（第2版）」

世界大百科事典（旧版）内の次元の言及

【異次元】より

…文学的空想における異世界alternate (other) worldと数学の次元概念dimensionとを合成した造語で，正しくは高次元的に存在可能な別世界とでもいうべきもの。近代SF文学のテーマとして盛んにとり上げられて以来，広く一般の関心を呼ぶようにもなった。われわれの空間は縦･横･高さの三次元に存在していると考えられているが，これに時間が加わって四次元の世界が存在しうると想像されており，位相幾何学的にはさらに五次元，六次元，n次元といった空間も式にすることができる。…

※「次元」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」