精選版 日本国語大辞典 「気体分子運動論」の意味・読み・例文・類語
きたいぶんし‐うんどうろん【気体分子運動論】
改訂新版 世界大百科事典 「気体分子運動論」の意味・わかりやすい解説
気体分子運動論 (きたいぶんしうんどうろん)
kinetic theory of gases
気体が多数の分子から構成されているという観点に立って,気体の示す諸性質を理解しようとする理論。18世紀から19世紀にかけて,D.ベルヌーイ,J.P.ジュールなどにより先駆的な仕事がなされ,C.マクスウェル,L.ボルツマンが理論体系を確立した。
容器に入れられた気体を考えると,この容器中には非常に多数の気体分子が含まれ,それぞれかってな熱運動をしている。すなわち,気体分子の熱運動はまったく乱雑であるとみなすことができる。マクスウェルはこの点に注目し,気体分子の速度分布が空間座標のx,y,z方向で独立であると仮定し,分子の速度分布を記述する法則を1860年に導いた。これをマクスウェルの速度分布則(マクスウェル=ボルツマン分布)という。ところで,気体分子が容器の壁に衝突してはね返されると,分子は壁に力を及ぼす。この力が気体の示す圧力の原因となる。気体分子運動論によると,分子と壁との衝突が弾性的であるとすれば,気体の圧力pは,
であることが示される。ただし,Vは容器の体積,Nは容器中の分子の数,mは気体分子の質量,〈v2〉は気体分子の速さvの2乗の平均値である。一方,ボイル=シャルルの法則により,1 molの理想気体に対してpV=RTの関係が成り立ち(Rは気体定数,Tは絶対温度),これと(1)式とを組み合わせると,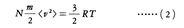
の関係が導かれる。(2)式の左辺は,気体分子の全運動エネルギーを表し,1 molの理想気体がもつ内部エネルギーに等しい。この関係からエネルギー等分配の法則を導くことができる。
気体分子運動論は,上述のような熱平衡状態にある気体の性質だけでなく,熱伝導率,粘性係数,拡散係数など輸送現象と関連した物理量の研究に拡張することもできる。これらの利点は,現代の物理学でも生き残っており,例えば固体中の電気伝導を取り扱う際,気体分子運動論における種々の計算方法が役に立っている場合が多い。気体分子運動論が物理学に与えた影響として,平均とか統計といった確率的な概念が物理学の中に導入された点が挙げられる。例えば,ニュートン力学で1個の質点の運動を考えるときには,最初に質点の位置・速度を決めれば以後の運動は一義的に決定され,確率といった概念の入り込む余地はない。しかし,気体中の分子はきわめて多数であるために,力学的な記述はあまり役に立たず,気体の巨視的性質を調べるには,なんらかの意味で統計的な要素が必要となってくる。このような思想は,さらに一般化されて統計力学の建設をうながす大きな要因となった。
執筆者:阿部 龍蔵
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「気体分子運動論」の意味・わかりやすい解説
気体分子運動論
きたいぶんしうんどうろん
分子の集まりである気体の熱力学的性質を、ミクロな運動から説明しようとする理論。18世紀にはD・ベルヌーイなどによってボイル‐シャルルの法則や内部エネルギーの温度変化などの諸性質について、独立の粒子が壁と弾性衝突をするモデルで説明された。ここで、一辺がLの立方体の容器に閉じ込められた気体を考える。分子の質量をm、分子の壁に垂直な成分をvとすると器の壁に分子が衝突して跳ね返るときに与える力積は2mvであり、分子は単位時間当り壁の間をv/2L回往復するので、この分子が単位時間当り壁に与える力積はmv2/Lである。壁が単位時間、単位面積当りの気体から受ける力積はこれらを集めたものであるので粒子数をNとするとNmv2/L3である。分子には速いものも遅いものもあるが、ここではその平均値をとって考える。また、内部エネルギーは3方向の運動エネルギーの和であるのでU=3Nmv2/2である。ここで、エネルギーの等分配則mv2/2=kBT/2を用いると
が得られる。
実際の気体での輸送現象を議論するためには、分子間の衝突の効果をとり入れ、衝突せずに進む距離(平均自由行程)を用いて粘性や熱伝導率が議論される。詳しい気体の熱力学的性質は、統計力学を用いてビリアル展開などの形で研究が進められている。
[宮下精二]
化学辞典 第2版 「気体分子運動論」の解説
気体分子運動論
キタイブンシウンドウロン
kinetic theory of gas
気体分子の運動を論じることから出発して,気体の性質を導いていく理論体系.D. Bernoulli(1738年),J.P. Joule(1851年),K.A. Krönig(1856年)によりはじめられ,R.J.E. Clausius(クラウジウス)(1857~1862年),J.C. Maxwell(1859~1866年),L. Boltzmann(1868~1876年)らによって発展され,今日では統計力学の重要な一部門になっている.気体では液体や固体とは違って,分子間距離が分子の大きさに比べて大きいので,もっとも簡単には相互作用のない剛体球の集りとみなすことができる.気体の圧力はこれらの剛体球が壁と衝突するときの運動量変化の平均値とみることができ,理想気体の法則が導かれる.また,分子の運動を統計的に扱うことによって,任意の温度における気体分子の速度分布関数(マクスウェルの速度分布則)を求めることができる.この法則を使って,気体分子の平均速度,平均自由行程,衝突数,さらには比熱容量などの熱力学的量も得られる.また,ある平均自由行程をもって分子相互の衝突が起こってはじめて物質,運動量およびエネルギーの移動があるので,拡散,粘性,熱伝導などの現象もこの理論から説明される.しかし,拡散,粘性,熱伝導などの実験値は,分子間相互作用を無視した理論では十分には説明できない.分子間相互作用も考慮できるように理論を検討しなおしたのは,D. Hilbert(1912年),D. Enslog(1917年),S. Chapman(1916~1917年)らである.これらの理論は,金属の電子論や気体中の放電現象についても応用され,なお発展を続けている.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
百科事典マイペディア 「気体分子運動論」の意味・わかりやすい解説
気体分子運動論【きたいぶんしうんどうろん】
→関連項目気体|平均自由行路
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「気体分子運動論」の意味・わかりやすい解説
気体分子運動論
きたいぶんしうんどうろん
kinetic theory of gases
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の気体分子運動論の言及
【気体】より
… 一方,気体は多数の分子から構成されるという観点に立って,気体の示す諸性質を理論的に解明しようとする試みがなされてきた。これを気体分子運動論という。この理論はさらに一般化され,統計力学という一つの理論体系へと発展した。…
※「気体分子運動論」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
ローマ法王ともいう。ラテン語 Papaの称号はカトリック教会首長としてのローマ司教 (教皇) 以外の司教らにも適用されていたが,1073年以後教皇専用となった。使徒ペテロの後継者としてキリスト自身の定...

