精選版 日本国語大辞典 「波動力学」の意味・読み・例文・類語
はどう‐りきがく【波動力学】
改訂新版 世界大百科事典 「波動力学」の意味・わかりやすい解説
波動力学 (はどうりきがく)
wave mechanics
電子はニュートン力学で記述されるような質点ではなく,光と同様に波動である。1924年ド・ブロイは電子の波動説を唱え,電子の運動量pとそれに付随する波動の波長λとの間の関係λ=h/pを与えた(hはプランク定数)。これは実験によって確かめられた。26年,E.シュレーディンガーは電子の波動の従うべき方程式(シュレーディンガー方程式)を導き,これによって電子のふるまい,とくに水素原子のエネルギー準位をみごとに説明した。
このシュレーディンガー方程式によって記述される電子の力学が,波動力学である。
シュレーディンガーの波動方程式は次のようにして与えられる。古典力学により電子を記述し,その座標をxi,共役な運動量をpi,ハミルトニアンをH(xi,pi)とする。その表式においてpiを微分演算子(ħ/i)(∂/∂xi)でおきかえる。ここでħはプランク定数を2πで割ったものである。こうして得られる演算子,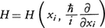 を(量子力学的)ハミルトニアンと呼ぶ。xiと時間tの関数ψ(xi,t)に対する微分方程式,
を(量子力学的)ハミルトニアンと呼ぶ。xiと時間tの関数ψ(xi,t)に対する微分方程式,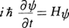 がシュレーディンガーの波動方程式である。波動関数がψ(x,t)=exp(-iEt/ħ)φ(x)の形のものを定常状態と呼び,方程式は固有値問題,
がシュレーディンガーの波動方程式である。波動関数がψ(x,t)=exp(-iEt/ħ)φ(x)の形のものを定常状態と呼び,方程式は固有値問題,
Hφ=Eφ
となる。
これもシュレーディンガー方程式と呼ばれる。固有値Eは系のエネルギー準位を与える。1個の電子に作用するポテンシャルエネルギーをV(x)とするとき,方程式は,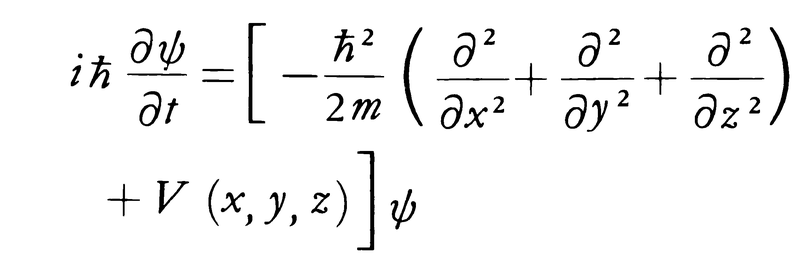
である(mは電子の質量)。波動ψが空間的に小さい領域に集中した波束となっているときは,波束の中心はポテンシャルVの中の質点の運動と同じように動く(エーレンフェストの定理)。すなわち,シュレーディンガーの波動は小さい波束になったときは近似的に質点のようにふるまい(対応原理),波動としてはド・ブロイの関係に従うものである。
波動関数ψの物理的意味に関しては,当初多くの議論がなされた。これが三次元空間の実在の波動を表すのか否かについてである。n体問題ではψ(x1,y1,z1,……,xn,yn,zn,t)という3n次元空間での波動を考えることになり,実在の波動では理解しにくい。M.ボルンはψに関し次の解釈を与え,これが今日受け入れられているものである。すなわち,波動関数の絶対値の2乗|ψ(x1,……,xn,t)|2は,ある時刻tで第1番目の粒子がx1に,第2番目の粒子がx2に,以下同じように第n番目の粒子がxnに見いだされる確率を与えるのである。観測により粒子がx1にあることが見いだされると,波動関数はx1のみで値をもつ集中した関数となる(波動の収縮)。しかしこれは確率波の収縮であり,エネルギーが瞬間的に移動することを意味しない。全確率が1であることから,波動関数は,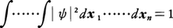 と規格化される。運動量pと座標xの関数である物理量A(x,p)の,ある状態ψでの平均値〈A〉は,
と規格化される。運動量pと座標xの関数である物理量A(x,p)の,ある状態ψでの平均値〈A〉は,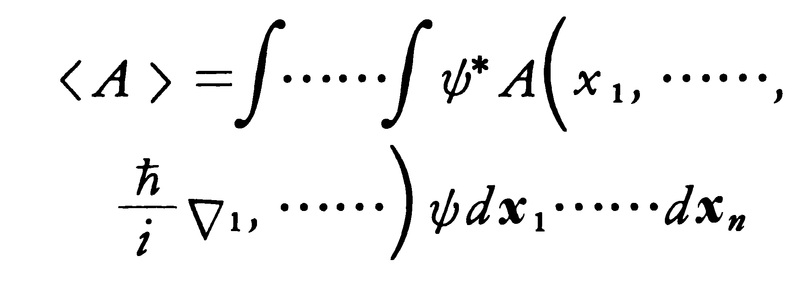
で与えられる(ψ*はψの複素共役量,∇はナブラと呼ばれる微分演算子)。
シュレーディンガーの波動力学は,W.K.ハイゼンベルクのマトリックス力学と同じ結果を与える。P.A.M.ディラックは変換理論により両者は同等であることを示した。すなわち,波動力学もマトリックス力学も,量子力学と呼ばれる理論を異なる形式で表現したものである。マトリックス力学は行列という数学形式を用いたのであるが,波動力学は偏微分方程式により具体化したもので,このほうが数学的に扱いやすい。そこで原子・分子の量子力学では波動力学の形式が利用される。
→量子力学
執筆者:宮沢 弘成
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「波動力学」の意味・わかりやすい解説
波動力学
はどうりきがく
wave mechanics
原子・分子や原子核・素粒子の領域では、古典力学が成り立たず量子力学が支配している。波動力学はこの領域の運動状態の波動的側面に注目して構成した量子力学の形式の一つであって、行列力学と対照的な形式である。しかし両者は互いに同等な量子力学の理論であって、表現が異なるだけであることが示されている。
1926年、シュレーディンガーは、ド・ブローイが提唱した電子の波動を幾何光学の類推に基づいて拡張し、ポテンシャルの作用を受けている場合の電子の波動方程式すなわちシュレーディンガーの波動方程式を導いた。ここでは電子の運動量・エネルギーおよび電子の受けるポテンシャルに対して波動の波数(波長の逆数)、振動数および屈折率が対応している。
量子力学に従った運動状態、すなわち量子的状態として異なるものを重ね合わせたものも一つの量子的状態である。この重ね合わせ可能という特徴は量子的状態の本質的な内容であって、しかもこれは波動一般の特徴でもある。量子的状態の運動方程式が波動の方程式の形をとることができるのも、このことに基づいていると考えられる。行列力学が物理量を行列として表現しているのに対して、波動力学は量子的状態を連続的な波動として表現することができる。このため量子力学の形式としてもっともよく用いられるが、行列力学と波動力学とは同等であることが示されており、物質が波動であるとは考えられていない。
[田中 一・加藤幾芳]
『ルイ・ド・ブロイ編、今泉正訳『波動力学および分子生物学』(1964・白水社)』▽『湯川秀樹監修、田中正・南政次訳『シュレーディンガー選集1 波動力学論文集』(1974・共立出版)』▽『カール・プルチブラム著、江沢洋訳『波動力学形成史――シュレーディンガーの書簡と小伝』(1982・みすず書房)』▽『武谷三男・長崎正幸著『量子力学の形成と論理3 量子力学の成立とその論理』(1993・勁草書房)』▽『小出昭一郎・阿部龍蔵監修、江沢洋著『量子力学1』(2002・裳華房)』▽『ジャン・ルイ・デトゥーシュ著、鈴木周夫訳『波動力学』(白水社・文庫クセジュ)』▽『吉田武監修、高林武彦著『量子論の発展史』(ちくま学芸文庫)』
百科事典マイペディア 「波動力学」の意味・わかりやすい解説
波動力学【はどうりきがく】
→関連項目空孔理論|ド・ブロイ|パリティ|ボルン
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「波動力学」の意味・わかりやすい解説
波動力学
はどうりきがく
wave mechanics
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
化学辞典 第2版 「波動力学」の解説
波動力学
ハドウリキガク
wave mechanics
量子力学の一形式.1926年にE. Schrödingerがド・ブロイ波の考えを発展させ,粒子の状態を波動関数で表すことを試み,いわゆる水素原子のシュレーディンガー方程式を提出し,その解から水素原子の発光スペクトルの説明に成功した.その後,波動力学は,1925年にW. Heisenbergによって提出されていた行列力学と物理的には同じ内容をもつことがSchrödinger自身によって証明された.波動力学は行列力学よりもなじみやすいので,量子力学を用いるあらゆる分野で幅広く使われている.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
世界大百科事典(旧版)内の波動力学の言及
【量子力学】より
…この考えは,結局,エネルギーEと運動量pをもつ電子に振動数ν=E/hと波長λ=h/pの波動を付随させることに落ちつき,この波動は物質波ないしド・ブロイ波とよばれることになった。
[波動力学]
ド・ブロイは物質波の位相しか問題にしなかった。波動を扱うなら波動方程式をというP.デバイの示唆にこたえて,1926年にE.シュレーディンガーが波動力学をつくった。…
※「波動力学」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
目次 飼養文化 北アメリカ 北方ユーラシア偶蹄目シカ科の哺乳類。北アメリカでは野生種はカリブーcaribouと呼ばれる。角が雄だけでなく雌にもふつうある。体長130~220cm,尾長7~20cm,...

