翻訳|temperature
精選版 日本国語大辞典 「温度」の意味・読み・例文・類語
おん‐どヲン‥【温度】
- 〘 名詞 〙 冷温の度合を表わす語。また、その度合。温度の高低を測る尺度に摂氏、華氏、絶対温度などがある。欧米では日常生活には華氏目盛が、科学用には摂氏目盛が用いられているが、日本では摂氏目盛のみが用いられる。
- [初出の実例]「同く気温六十度の室に置けば漸く皆同一の温度と為るなり」(出典:舎密開宗(1837‐47)初)
温度の語誌
「舎密開宗」には、「温度」のほか「熱度」も使用された。明治三〇年代まで、「温度」も「熱度」も共に気温など熱さの値を表わす語として用いられていたが、その後、「温度」が一般的な表現となり、「熱度」は体温など限られた意味にしか使用されなくなった。→熱度
改訂新版 世界大百科事典 「温度」の意味・わかりやすい解説
温度 (おんど)
temperature
温度とは熱い冷たいの度合であり,物理的には巨視的な物体の熱平衡状態を特徴づける量である。二つの物体を接触させると,熱は温度の高いほうの物体から低いほうに移り,最終的には両者の温度は等しくなる。
温度概念の形成
温度の概念は人間が皮膚で感ずる熱い,冷たいという感覚に由来する。すでにギリシア時代から熱さ,冷たさの度合をそれぞれ数個の段階で表すことが医学で行われていたが,連続的な量として考えるようになったのは近世になってからである。それ以前には冷と暖は乾と湿のように対立する要素であり,冷気と熱気の混り方が実際の暖かさを作り出すという考えが支配的であった。ラテン語で温度を意味するtemperaturaも,もともとは“混り方”という意味である。空気の熱膨張を示す装置はギリシアのフィロンやヘロンが考案していたが,16世紀の終りごろになって初めてガリレイらはそれを温度計として利用した。17世紀になると気体温度計も改良され,またアルコールを使った液体温度計も現れ,ヨーロッパでは医者の診断や気温を測るのに広く使われるようになった。18世紀ころからは,各地の気温を比較する必要などのため,定量的測定の可能な目盛のある温度計が作られるようになり,氷の融点などを温度の定点とする提案がなされた。G.D.ファーレンハイトは1717年ごろに水銀温度計を製作し,水,氷,食塩を混ぜて得られる温度を0度,氷の融点を32度,体温を96度とする華氏温度目盛を考案し,42年にはA.セルシウスが氷の融点を0度,水の沸点を100度とする摂氏温度目盛(セルシウス度)を導入した。以後,温度計と温度目盛の改良は熱学の発展を促すことになった。
18世紀の半ばに行われたJ.ブラックらによる比熱の研究は,熱と熱さすなわち温度との区別を意識させた。また19世紀初めごろまでにJ.L.ゲイ・リュサック,J.ドルトンらは,多くの気体の熱膨張係数がすべて同じ値であることを確かめ,以前からG.アモントン,W.アービンらが推測していた温度の下限,すなわち気体から熱が完全に奪われて圧力が0になる温度の値が摂氏でおよそ-270度であると主張した。このころから熱学は急速に発展し,19世紀後半に熱力学の第1法則,第2法則が認識されるに至って,温度は熱と区別された明確な概念となり,同時に普遍的な意味をもつ絶対温度の基礎も与えられた。さらに20世紀にかけて発展した気体分子運動論,統計力学により,熱現象を原子,分子の運動に基づいて理解することが可能となり,温度の意味もこのレベルで明らかになった。
→温度計
経験的温度
物体を外界から孤立させて放置すると何の変化も認められない熱平衡状態になる。また二つの物体を熱のやりとりだけが生ずるように接触させると,熱いほうの物体から冷たいほうへ熱が移り,物体の状態が変化するが,十分長い時間がたつとやはり熱平衡状態になる。このとき二つの物体の温度は等しいというが,温度が意味をもつのは熱力学の第0法則と呼ばれる法則,すなわち,三つの物体A,B,Cがあり,AとBおよびAとCとが互いに熱平衡にあるならば,BとCも互いに熱平衡にあるという法則が成り立つからである。ある物体Aを温度計とし,温度によって変化するAの量をtとする。例えば気体温度計なら一定体積の気体の圧力,水銀温度計なら水銀柱の長さ,抵抗温度計なら電気抵抗などである。Aを他の物体B,C,……と熱接触させて平衡になったときのtの値を測り,B,C,……の温度とする。BとCの温度tの値が等しければ上の法則によって両者を熱接触させても何の変化も生じない,すなわち互いに熱平衡の状態にあることがわかる。
個々の温度計で測る量tを経験的温度という。経験的温度は個々の温度計に固有の量であるから,相互の関係をつけなければならない。そのために1気圧下での氷の融点あるいは水の沸点など特定の現象,とくに潜熱を伴う相変化の生ずる温度を温度の定点とする。例えば摂氏温度目盛では氷の融点を0度,水の沸点を100度と定める。このようにして定点での温度計のtの値を決めても,定点の間を等分してつけた目盛はやはり個々の温度計特有のものである。水銀温度計では摂氏0度と100度での水銀柱の高さの差を100等分するが,そうして得られる目盛とアルコール温度計で同様にしてつけた目盛とは,水銀とアルコールの熱膨張のしかたが異なれば一致しないのである。またどんな温度計も限られた範囲でしか使えない。そこで個々の物質の性質によらない普遍的な意味をもつ温度が考えられるかという問題になるが,絶対温度はそれに答えるものである。
絶対温度
絶対温度は熱力学の第1法則および第2法則に基づいて次のように定められる温度で,熱力学的温度ともいう。第1法則によると熱はエネルギーの一形態であり,蒸気機関などの熱機関によって仕事,すなわち力学的エネルギーに転換される。第2法則によるとどんな熱機関も高温と低温の熱源を必要とする。ある熱機関が高温の熱源から熱Q1を受けとり,低温の熱源にQ2の熱を放出することによって仕事Wを行い,最初の状態にもどるとする。エネルギー保存則からW=Q1-Q2であるから,高温の熱源からとった熱Q1のどれだけが仕事Wにかえられたかという熱機関の効率ηは,
η=W/Q1=1-(Q2/Q1)
である。同じ二つの熱源を使って働く熱機関の中でもっとも効率のよい,すなわち理想的な熱機関の効率は,二つの熱源の温度だけで定まるはずである。そこで,理想的な熱機関の場合の効率を決める比Q2/Q1を二つの熱源の絶対温度の比と定義する。すなわち高温と低温の熱源の絶対温度をそれぞれT1,T2とすると,T2/T1=Q2/Q1である。この関係によって,絶対温度は比例定数を除いて決定される。したがって温度の定点を一つ選び,その値をT0と決めれば,温度T0の熱源を,例えば高温熱源にする理想的な熱機関を働かせ,Q1,Q2を測定すれば低温熱源の絶対温度がT=T0Q2/Q1と定められる。なお,効率ηは1を超えることはありえないから絶対温度には下限すなわち絶対0度が存在する。このような絶対温度の概念は1848年にW.トムソン(ケルビン)によって導入された。理想的な熱機関とは可逆的に働く熱機関で,カルノーサイクルに代表される。上で絶対温度の比を定義した関係はQ1/T1=Q2/T2と書きなおされ,可逆過程でエントロピーS=Q/Tが保存されることを表している。絶対温度はエントロピーという重要な量の導入を可能にしたのである。
理想的な熱機関は実現不可能であり,また温度の測定に熱機関を使うのは実用的でない。したがってまず熱力学および統計力学を用いていろいろな温度計の示す経験的温度と絶対温度との関係を求める。例えばどんな気体も十分希薄にすると理想気体とみなせ,その体積Vと圧力Pとの積は絶対温度Tに比例する,すなわちPV=RTであることがわかっているから(Rは気体定数),気体温度計で絶対温度の測定ができる。実際には温度領域によって種々の異なる温度計が用いられるが,どの場合にも測定する物理量の温度変化の理論式が使われる。
温度目盛
現在使われている絶対温度目盛は,比較的安定に実現できる水の三重点を定点とし,これを273.16とする目盛である。この単位をケルビンと呼び,単位記号はKを使う。摂氏温度(℃)は1気圧での氷の融点273.15Kを0度とするから,摂氏温度tは,
t(℃)=T(K)-273.15
である。なお欧米で現在でも使われている華氏温度目盛での温度t′(°F)と摂氏温度の関係は,
t′(°F)=9/5t(℃)+32
である。国際実用温度目盛とは,水の三重点以外に,水素の三重点13.81K,酸素の三重点54.361K,銀の融点1235.08Kなどと温度の値を定め,さらに温度領域によって最適な温度計を指定し,それを標準とするものである。
→温度目盛
微視的にみた温度の意味
巨視的な物体は莫大な数の原子からできている。例えば常温常圧下の空気1cm3の中には約1019個の分子があり,1cm3の鉄は約1023個の原子を含む。気体分子は互いに衝突しながら乱雑なしかたで運動しており,また固体の中の原子はふつう規則的に並んでいるが,有限温度ではやはり乱雑な振動をしている。物質を構成する微視的な粒子のこのような乱雑な運動,すなわち熱運動のエネルギーが熱エネルギーにほかならない。熱運動は温度が高くなると激しくなる。希薄な気体の場合,個々の分子はいろいろな速度,したがって運動エネルギーで運動しているが,ある一つの分子がエネルギーEをもつ確率は,気体の温度をT(K)とすると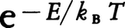 に比例し(マクスウェル=ボルツマン分布),平均のエネルギーは単原子分子の気体の場合3/2kBTで与えられる。ここでkBはボルツマン定数と呼ばれ,kB=1.38×10⁻23J・K⁻1に等しい。統計力学によると,一般に巨視的な物体においてエネルギーは気体のときと同様にそれを構成する非常に多くの粒子(正確には力学的自由度)に乱雑なしかたで分配されている。その分配の可能なしかたの数がエントロピーであり,エネルギーを大きくしたときエントロピーの増大する割合が絶対温度の逆数に比例する。どんな物体においても温度T(K)では,エネルギーがkBT程度で可能な運動(量子力学的には励起)が物体の中に乱雑に生じている。したがって温度を低くすると小さなエネルギーの微視的運動しか許されなくなり,物体全体のもつエネルギーも小さくなる。現実の気体では1分子当りの熱運動のエネルギー(~kBT)が分子間の引力のポテンシャルエネルギーより小さくなると分子どうしが集まって液体となり,さらに温度を下げるとふつうは固体になる。絶対0度では物体は最低エネルギーの状態にあり,乱雑な熱運動はなくなるからエントロピーは0となる(熱力学の第3法則)。逆に,どんな物体にも最低エネルギーの状態があるから,温度には下限すなわち絶対0度が存在する。一方,有限のエネルギーレベルしかもたない特殊な系を除くと,物質を構成する粒子はどんなに大きなエネルギーの運動もできるから,温度に上限はない。どんな物質も高温になると気体になり,5000度以上になると原子が電離し電子と原子核の気体,いわゆるプラズマになる。さらに100万度くらいになると原子核反応も生ずるようになる。絶対0度を実現することはできないが,原理的にはいくらでも近づくことはできる。現在0.1mK程度の極低温での実験が行われている。
に比例し(マクスウェル=ボルツマン分布),平均のエネルギーは単原子分子の気体の場合3/2kBTで与えられる。ここでkBはボルツマン定数と呼ばれ,kB=1.38×10⁻23J・K⁻1に等しい。統計力学によると,一般に巨視的な物体においてエネルギーは気体のときと同様にそれを構成する非常に多くの粒子(正確には力学的自由度)に乱雑なしかたで分配されている。その分配の可能なしかたの数がエントロピーであり,エネルギーを大きくしたときエントロピーの増大する割合が絶対温度の逆数に比例する。どんな物体においても温度T(K)では,エネルギーがkBT程度で可能な運動(量子力学的には励起)が物体の中に乱雑に生じている。したがって温度を低くすると小さなエネルギーの微視的運動しか許されなくなり,物体全体のもつエネルギーも小さくなる。現実の気体では1分子当りの熱運動のエネルギー(~kBT)が分子間の引力のポテンシャルエネルギーより小さくなると分子どうしが集まって液体となり,さらに温度を下げるとふつうは固体になる。絶対0度では物体は最低エネルギーの状態にあり,乱雑な熱運動はなくなるからエントロピーは0となる(熱力学の第3法則)。逆に,どんな物体にも最低エネルギーの状態があるから,温度には下限すなわち絶対0度が存在する。一方,有限のエネルギーレベルしかもたない特殊な系を除くと,物質を構成する粒子はどんなに大きなエネルギーの運動もできるから,温度に上限はない。どんな物質も高温になると気体になり,5000度以上になると原子が電離し電子と原子核の気体,いわゆるプラズマになる。さらに100万度くらいになると原子核反応も生ずるようになる。絶対0度を実現することはできないが,原理的にはいくらでも近づくことはできる。現在0.1mK程度の極低温での実験が行われている。
真空の温度
いままで物体の温度について述べてきたが,空間には電磁場があり電磁波という運動が可能である。したがって真空中には熱放射があり,有限温度の物体との熱平衡,すなわち真空の温度を考えなければならない。壁に囲まれた空洞を考えると,壁を作る原子が放射(電磁波)を放出したり吸収したりするため,壁と空洞内の放射の間に熱平衡が成り立つ。熱平衡にある放射のスペクトル密度,すなわち振動数と強度との関係は温度によって定まるプランクの放射則に従う。振動数νの電磁波はhν(hはプランク定数)のエネルギーをもつ光子とみなせるから,温度T(K)ではhνの値がほぼkBTの光子がもっとも多く,放射強度はこの関係で決まる振動数(正確にはν=2.8kBT/h)のところにピークをもつ。これを利用すれば真空の温度を求めることができる。炉に小さな穴をあけて中の色を見れば温度がわかるのはこのため。宇宙空間には宇宙の初期にあった放射に由来する約3Kの熱放射が観測されている。
執筆者:恒藤 敏彦
生物と温度
温度はあらゆる生命現象に直接の影響を及ぼす重要な環境要因である。温泉内に見いだされる微生物や藻類,極地の微生物や動物などは例外として,一般に生物が存在できる温度範囲は0~40℃である。しかしあらゆる生物がこの範囲全域にわたって生活できるわけではない。生物には個体維持や生殖のための最適温度と,それをはさんである一定の耐えうる温度範囲がある。いわゆる定温動物(哺乳類と鳥類)はこの温度範囲内では体温をほぼ一定に保って生活できるが,温度調節機能をもたない微生物,植物,変温動物などでは,外界の温度変化につれて生体の温度も変化するので,生体内のいろいろな反応は,定温動物と違って,直接外温の影響を受けることになる。生物反応速度に対する温度の影響は原則的には化学反応の場合と同じであり,それを表すのに生物学で広く用いられている指標に温度係数Q10というものがある。これは温度が10℃上昇したときの反応速度の増加率を示すもので,多くの生物反応のQ10値は2~3であるから,温度が10℃上昇するごとに反応は2~3倍に増加することになる。このほかには,アレニウスの式に出てくる活性エネルギー(Ea)も用いられる。種々の生物現象について調べられたEa値は1万~3万calの範囲の値を示している。
生物反応が一般の化学反応と著しく異なる点は,温度の上昇とともに反応速度の増加率はしだいに鈍り,ある程度以上の高温になると速度はかえって低下することである。これは生物反応の基盤となっている一連の化学反応で触媒の働きをする酵素タンパク質が熱によって変性し,その酵素活性を失うことが原因の一つであると説明されている。しかし,生体からとり出した酵素標品について調べてみると,酵素活性の熱阻害は生物反応速度が低下するよりも高い温度で起こることが多いため,必ずしも十分な説明とはいえない。
執筆者:佃 弘子
人体と温度
われわれをとり囲む環境において,外界の温度は重要な要因である。人体は体内の代謝および機能を円滑にすすめるために脳および軀幹(くかん)の温度を37℃近辺に恒常的に保つように,たくみに外界との熱収支のバランスをとっている。すなわち,外界の温度にあわせて体表面への末梢循環血液量を調節し,暑熱環境においては,循環器の働きに加えて発汗による蒸発熱により軀幹からの放熱を促進する。現在,人類はその生活の場を気象条件の厳しい極地,高山などや産業現場などにみられる高熱,寒冷な環境において生存,活動している。これを可能にしたのは,人体の適応,順化の能力の拡大ばかりでなく,被服,住居など人体を直接とり囲む環境を整える技術の開発に負っているところが大きい。適応,順化の例として,寒冷な夜間にはだかで睡眠をとることのできるアフリカのサンや,動物性タンパク質を主食とするエスキモー(イヌイット)があげられるが,われわれの身近においても,高熱作業に常時従事していてなんらの健康障害をも見いだされない労働者がいる。一方,われわれは被服で軀幹を包み外気温と直接接触することなく被服と皮膚の間に衣服気候を形成して体温調節の補助を有効に行っている。この衣服をまとった人体が生活する住居環境は,今日,暖房,冷房などの空気調節設備によって年間を通じて快適温度内に制御され,作業能率の向上,作業時間の延長を可能とした。かつて人類はその死亡率において季節による変動がみられたものだが,近年,寒冷な地域に位置する文化水準の高い国々では,冬季にとくに死亡率が高くなるという現象がみられなくなってきた。その理由は暖房設備の完備が大きな効果をあげていると推定されている。日本でも同様の傾向がみられる。人類の生存にとって,人体を直接とり囲む環境温度の重要性がこの面でも理解できる。外気温との熱収支のバランスに障害が起こると凍傷,冷房病,熱射病などに陥る可能性が考えられる。
→不快指数
執筆者:村上 正孝
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「温度」の意味・わかりやすい解説
温度
おんど
物体の寒暖の度合いを数量的に表すもの。気温、水温、体温というように、温度はわれわれの日常生活と密接に関係している量である。物理学的には物体間で熱のやりとりをする際に重要な役割を果たす熱平衡状態を指定するパラメーターの一つである。
[宮下精二]
温度の決め方
異なる温度をもつ状態の間には、熱の流れが生じて同じ温度になろうとする性質(熱力学の第二法則)がある。熱平衡状態では同じ温度になり、エネルギーのやりとりがつり合った状態になる。この性質を利用して、アルコールや水銀などの体積によって温度を定量化する温度計が可能となる。また、ボイル‐シャルルの法則を利用して気体の圧力P、体積Vを用いて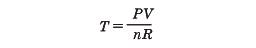
として決めるのが、気体温度計である。ここで、nは粒子数をモル数で表したもの、Rは気体定数である。実際、理想気体に近い気体を用いて、氷の溶ける温度を0℃、1気圧の大気中で水が沸騰する温度を100℃として、目盛りを決めたのが摂氏温度である。この決め方では、気体の体積がゼロになる温度は-273℃(正確には-273.15℃)となり、これを絶対零度という。また、絶対零度を基準として℃と同じ間隔で温度を目盛ったものを絶対温度目盛りという。現在では単にKの記号を使う。たとえば、0℃を絶対温度で表すと273Kとなる。異なる目盛りの取り方として、氷の溶ける温度を32度、水の沸騰する温度を212度とし、その間を180等分して1度とするのが華氏温度(かしおんど)である。
温度の定義で用いられた理想気体の内部エネルギーは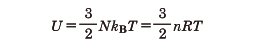
と表される。ここでNは粒子数、kBはそれぞれボルツマン定数である。アボガドロ数をNAとするとR=NAkBである。理想気体の内部エネルギーは個々の粒子の運動エネルギーの和であるため、この関係から、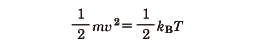
であることがわかる。このことから、温度は分子運動の激しさを表す量とみなすことができる。
温度の同定は必ずしも気体の体積によるものではなく、電気伝導度などによってもできるので、さまざまな温度計が可能となる。いわゆるデジタル温度計は電気的な性質を用いている。また、物質の色の変化を用いた温度計もある。
[宮下精二]
温度変化と物質の状態、性質
温度が上がると物体の内部エネルギーは上昇し、体積などが変化する。さらに、氷、水、水蒸気のように同じ物体でも温度によって巨視的な形態が変わることがあり、相転移とよばれる。上で述べた温度の目盛りを決める際にもこの相転移が起こる性質を用いた。しかし、実際に相転移点は圧力によって変わるため、正確な定義には氷、水、水蒸気が共存する三重点が用いられる。さらに、温度を上げ数万度になると分子は分解し、プラズマ化する。原子核が分解するにはさらに高い温度が必要となる。加速器では高速の粒子を衝突させ、非常に高い温度を実現し、物質の構造のより詳しい情報を得ようとしている。ただし、そのような場合は熱平衡状態の温度というより、平均運動エネルギーをp2/2m=1/2kBTで換算した値というべきである。また、宇宙の始まりのビッグ・バンは非常に高い温度から出発し、膨張によって諸物質が生成されたとされ、現在の温度は3Kであるとされる(2012年時点)。この温度は、宇宙からの放射のスペクトルから決められたものである(「宇宙背景放射」「プランクの放射公式」の項参照)。
電気抵抗も温度によって変化する。電気伝導を担う金属内の電子は格子の熱振動で妨げられるため、温度が上がると電気抵抗は大きくなる。しかし、半導体とよばれる物質では、温度が高くなると電気伝導を担う電子や正孔の数が増え、電流が流れやすくなる。また、超伝導とよばれる現象は電子の運動に関する量子力学的な相転移である。
[宮下精二]
温度と生物
温度は生物の各種の生理作用に影響を及ぼす。生体内の化学反応や生理作用が、温度によってどれだけ変わるかを示すのに温度係数が使われる。たとえば、ジャガイモの葉の同化作用は5℃近傍では、温度が1℃上がるたびに1.27倍になる。この1.27という数値がこの場合の温度係数である。一般に、化学反応の反応速度は、物質の濃度が同じであれば、温度が10℃上昇すると2~3倍になる。この倍数も温度係数とよばれる。
われわれが実際に感覚する温度は、かならずしも物理的な温度と一致しない。気温が同じ30℃であっても、風があるかないか、湿度が高いか低いかなどによって温度の感じ方が異なってくる。とくに湿度が高いと蒸し暑く感じるが、このような感覚を表す量としてよく不快指数が用いられる。
[阿部龍蔵・宮下精二]
ブリタニカ国際大百科事典 小項目事典 「温度」の意味・わかりやすい解説
温度
おんど
temperature
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「温度」の意味・わかりやすい解説
温度【おんど】
出典 株式会社平凡社百科事典マイペディアについて 情報
化学辞典 第2版 「温度」の解説
温度
オンド
temperature
温度はもともと人間が感じる寒暖の度合を示すことばであるが,物理的には物体の熱的平衡状態を特徴づける量として定義される.A,B二つの物体が接触しているとき,AからBへ,あるいはBからAへ熱が流れないとき,二つの物体は等しい温度にあるという.AからBへ熱が流れるときは,AはBより温度が高いという.温度の高低を数量的に表すために,温度目盛が定められている.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
栄養・生化学辞典 「温度」の解説
温度
関連語をあわせて調べる
目次 飼養文化 北アメリカ 北方ユーラシア偶蹄目シカ科の哺乳類。北アメリカでは野生種はカリブーcaribouと呼ばれる。角が雄だけでなく雌にもふつうある。体長130~220cm,尾長7~20cm,...

