相対性理論（読み）ソウタイセイリロン（その他表記）relativity theories

デジタル大辞泉

そうたいせい‐りろん〔サウタイセイ‐〕【相対性理論】

アインシュタインによって確立された物理学の基礎理論。1905年発表の特殊相対性理論は、光速度がすべての観測者に対して不変であることと相対性原理に基づいて、互いに等速度運動する観測者どうし（慣性系）に対して、電磁気学を含むすべての物理法則が同じ形で成立することを定式化したもの。この理論によると、時間は観測者によって異なるという相対的なものとなる。1915年発表の一般相対性理論は、等価原理と相対性原理に基づいて、互いに加速度運動する観測者どうし（加速系）を含む全座標系に対して、すべての物理法則が同じ形で成立することを定式化したもの。これによって万有引力の現象が説明された。

出典　小学館

共同通信ニュース用語解説

相対性理論

アインシュタインが20世紀初めに完成させた物理学の理論で特殊と一般の二つがある。量子力学とともに現代物理学の根幹をなしている。特殊相対性理論は、光の速度は不変とする原理を唱え、高速で移動する物体では時間の進み方が遅くなるなどとした。この理論に重力を取り込み、より一般化したのが一般相対性理論。重い物体の周囲では空間がゆがみ、光も曲がって進むなどと考えた。物体が動いたときに、時間や空間の揺れが波となって広がるのが重力波とされる。(共同)

更新日:2016年2月11日

出典　共同通信社 共同通信ニュース用語解説

精選版 日本国語大辞典

そうたいせい‐りろんサウタイ‥【相対性理論】

1. 〘 名詞 〙 物理学者アインシュタインによって提唱された物理学の基礎理論。一九〇五年に発表された特殊相対性理論と、一五年に発表された一般相対性理論とからなる。特殊相対性理論は、光速度が座標系の速度によらず常に一定値をとる事実をもとに、互いに等速直線運動をしている観測者（慣性系）に対し、すべての物理法則が同じ形で成立するよう定式化したもの。一般相対性理論は、加速度をもつ観測者同士にも相対性の原理が成立するよう一般化したもので、重力の場を含むあらゆる座標系に対して成り立つことから万有引力の現象を説明する。この理論によると、運動の絶対の基準であった時間・空間は、観測者に対してだけ意味をもつ相対的なものとなり、従来の概念を根本的に変更した四次元の新しい時間・空間構造をもたらした。相対性原理。相対論。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

相対性理論
そうたいせいりろん
relativity theories

アインシュタインにより提唱された特殊相対性理論と一般相対性理論の総称。特殊相対性理論は、ニュートン力学と光の電磁気理論との矛盾を時間・空間の考え方に新概念を導入して解決したもので、1905年に発表された。この理論は電磁気の理論の基礎を明らかにしたばかりでなく、その後に発展した原子核・素粒子の研究の手段として活躍した。一般相対性理論は、1916年に完成された理論で、重力の相対論的理論の一つであり、特殊相対性理論と異なり、まだ完全に実証された理論ではない。

　物理法則が、それを表現する座標系が変換しても形が不変であるところから、あらゆる座標系は互いに対等であり、相対的であるというのが相対性理論の意味である。「特殊」とは、この座標系の変換を等速運動という特殊なものに限っているという意味であり、「一般」とは、加速度をも含む一般運動の変換に一般化されているという意味である。

　一般相対性理論は、重力が支配的な役割を演ずる宇宙現象、とくに膨張宇宙論やブラック・ホールなどの解明に大きく寄与している。また、素粒子物理学における力の統一理論（統一場理論）の試みのなかでも重要な理論になっている。

［佐藤文隆］

ガリレイの相対性原理

ニュートン力学にも相対性理論が存在するが、この理論の基礎の一つは、ガリレイによって最初にみいだされた慣性の法則である。すなわち、力が働かなければ運動量（質量と速度の積）は一定にとどまるという法則である。この法則が成り立つ一つの座標系Kがあったとして、このKに対して等速運動をしている座標系K'においても慣性の法則が成立する。運動の方向をx座標方向に選ぶとすれば、K系の座標(t,x,y,z)とK'系の座標(t',x',y',z')との間には一定速度をvとして
　　t'＝t, x'＝x－vt,
　　y'＝y, z'＝z　　　(1)
の関係がある。

　ニュートン力学の第二法則は、力（F）と加速度（a）の間にma＝Fの関係があるというものである。ここでmは質量。K系とK'系では加速度は変化しないため、a'＝aであり、この法則はこのような座標変換に対して不変にとどまる。このことを、(1)式のようなガリレイ変換に対して、ニュートン力学は相対性原理を満たすという。また、このような相対性原理はガリレイの相対性原理ともよばれる。

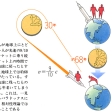
　この問題の発端は、ガリレイの地動説とも関連している。コペルニクス説は、その後の宇宙論と物理学にさまざまの影響をもたらしたが、その一つが地動説である。ガリレイはこの問題を地上における運動学の問題と同一次元で論ずることによって、慣性の法則を発見したのである。地球が秒速30キロメートルの高速で動いているにもかかわらず、その運動を容易に感知することができないことの説明は、この相対性原理によって初めて可能なのである。ガリレイは『天文対話――プトレマイオスとコペルニクスとの二大世界体系についての対話』（1632）という著書において、第2日目の討論でこの問題を取り上げている。そのなかで、ガリレイは、大地の運動と船の運動を対比させて、いかにこれらの等速運動を感知するのが不可能であるかを説いている。

［佐藤文隆］

光とエーテル

光は干渉や回折をする現象から、振動であることが認識され、光の電磁気理論はこれを電場・磁場の振動として記述することに成功した。初め、この振動は空間に充満している媒質の力学的運動の結果として生ずるものと考えられ、このような仮想的な振動媒質にエーテルという呼び名が与えられた。光は他の星からもやってくるため、このエーテルは宇宙空間にも充満しているはずであると考えられた。

　一方、地球も他の天体も、このエーテルに対して一般には運動をしている。したがって、エーテルにおこっている振動を、それに対して異なった運動をして観測すれば、一般に振動は異なってみえる。この原理を用いて、エーテルという電磁波の媒質の静止系をみいだそうという試みが、19世紀後半にいくつも行われたが、これらはすべて失敗に帰した。たとえばフィゾーは、流れる水にエーテルが引きずられるかどうかを実験し、マイケルソンとE・W・モーリーは、地球の運動方向によって光の速度がどう異なるかの実験を行っている。

［佐藤文隆］

アインシュタインの特殊相対性理論

もしも光の現象を通じてエーテル静止系が観測されたとすれば、それは光の現象、さらにその基礎である電磁気現象について、相対性原理が成立しなくなることを意味する。なぜなら、エーテル静止の座標系は一つの絶対的な意味をもち、すべての座標系が対等でなくなるからである。しかし、エーテル静止系は発見できなかった。相対性原理は依然として成立しているのである。ところが、マクスウェルの電磁気学は、ガリレイ変換に対する相対性原理を満たしていない。このような、ニュートン力学と、当時は新興の理論であった電磁気学との間の矛盾は、H・A・ローレンツやJ・H・ポアンカレによっても指摘されていた。

　こうした状況のなかで、アインシュタインは、この矛盾の解決法を時間・空間の新しい概念に求め、
〔1〕新しい相対性原理が力学と電磁気学をも含むすべての物理法則に対して成立する
〔2〕光の速さは慣性系で一定である
の二つを基礎に特殊相対性理論を築いた。ここで慣性系とは、力が働かなければ一定速度で運動するような座標系をいう。

　特殊相対性理論では、座標変換は(1)式のガリレイ変換ではなく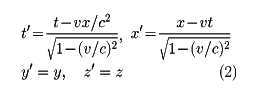

というローレンツ変換式に変更しなければならない。これにより電磁気学はこの座標変換に対して不変であり、力学法則はこれに対して不変であるように変更された。(2)式は速度vが光速cに対して十分に小さければ、近似的に(1)式に一致することになる。このことからもわかるように、変更された相対論的な力学は、速度が光速に比べて十分小さければ、ニュートン力学の法則と近似的に一致する。しかし、電磁気学にはつねに光速が関与しているため、ニュートン力学のような非相対論的な近似理論は存在しない。

［佐藤文隆］

同時刻の相対性

ローレンツ変換式(2)の特徴は、時間も座標変換によって変換されることである。このため、離れた場所における二つの事象の同時性が相対的になる。たとえば、K系のA点(x_A,0,0)とB点(x_B,0,0)で同時刻t_A＝t_Bに、ある事象がおきたとする。ところが、(2)式によればt_A'≠t_B'になる。すなわち、K'系ではこれらの事象は同時におきていないことになる。同時刻であるかどうかは座標系によって異なる相対的な概念なのである（図A）。

　同時刻の相対性は必然的に長さの相対性をも引き起こす。ある棒の長さは、両端が同時にある空間座標の差で決まる。ところが、両端の同時性は、それを観測する座標系によって異なる。したがって、棒が運動してみえる座標系で測った長さは、速度によって変化することになる。速度vで運動している棒の長さlは、静止している場合の長さl₀に比べて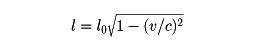

のように短くなる。これをローレンツ収縮という。

　また、(2)式でわかるように、K系に静止している物体で、経過する時間TとK'系における時間T'との間には、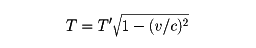

の関係がある。K'系からみれば、この物体は動いているため、動いている物体のうえでは事象がゆっくり進行することを表している（図B）。たとえば、ある寿命で崩壊する素粒子の寿命は運動していると長くなる。

［佐藤文隆］

速度の合成則

ある物体のK系における速度wとK'系における速度w'の間には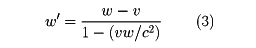

という速度の合成則が成り立つ。特別な場合として、w＝cとすればw'＝cとなり、どの座標系でも光速は一定であることが確かめられる。これは、光が静止してみえる慣性系は存在しないことを意味する。すべての慣性系では光速は一定であるという法則が成立するのである。つまり、光速に近い速度で運動する素粒子が崩壊して光を発する場合も、けっして速度の加算になるのではなく光速のままであることが、実験により検証されている。

［佐藤文隆］

質量エネルギー

力学法則は特殊相対性理論に適合するように修正されたが、その結果、明らかになった重要な概念に質量エネルギーがある。これは質量mとエネルギーEは等価であって、E＝mc²のエネルギーを含むということである。運動量pの粒子の全エネルギーは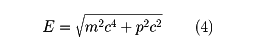

で表される。光は質量がゼロの粒子として扱われる。

　アインシュタインの関係式(4)は、原子核からの放射能エネルギーや素粒子の生成・消滅を理解する基礎を与えた。原子力エネルギーは、質量のわずかな部分がエネルギーに転化するものとして理解できる。また、γ(ガンマ)線により電子・陽電子対が生成される過程は、γ線のエネルギーが電子の質量エネルギーに転化したものとして理解される。また特殊相対性理論は、素粒子を場によって記述する基礎をも与えた。こうして質量をもつ素粒子も質量ゼロの光も同等に扱うことが可能になり、量子力学の確立とあわせて、今日における素粒子像の形成をもたらした。

［佐藤文隆］

ミンコフスキー空間

ローレンツ変換式(2)より
　　－c²t'²＋x'²＋y'²＋z'²
　　　＝－c²t²＋x²＋y²＋z²
を確かめることができる。これは、時間と空間をいっしょにした四次元空間における「長さ」が、ローレンツ変換によって不変であることを示している。ただし、ここで「長さ」はユークリッド空間（縦、横、奥行の三次元の空間）の場合と異なり、2点間の座標差をdx^μ(μ＝0,1,2,3)とすれば「長さ」の2乗ds²は
　　ds²＝η_μνdx^μdx^ν　(5)
で表される。ここで添字μ、νは0から3までの和をとる。計量テンソルη_μνは、
　　η₀₀＝－1,η₁₁＝η₂₂＝η₃₃＝1
で、その他はゼロである。「長さ」がこのような計量テンソルで与えられる四次元の空間を、ミンコフスキー空間とよぶ。ローレンツ変換は、この空間における一種の回転として理解される。特殊相対性理論は、1907年のミンコフスキーによるこのような認識によって完成されたといえる（図C）。

［佐藤文隆］

ローレンツ群と素粒子

ミンコフスキー空間における回転変換のローレンツ群に対して不変な表式が物理法則であるというのが、この理論の到達点である。そこで、このローレンツ群と等価な群に従うスピンという量が、ディラックにより導入され、このスピンは反物質の存在を明らかにし、電子などの素粒子を記述する場であることがわかった。このように、ローレンツ群に対する不変性の要請（公理）は、単に法則が従うべき規範であるだけでなく、物質存在そのものを演繹(えんえき)する法則として活躍したのである。さらに相対性原理から出発した法則の規定の仕方である、変換群に対する不変性の要請は、その後、時間・空間座標の変換を離れて広く用いられるようになった。

　この考えは対称性の理論とよばれる。現在では、特殊相対性理論もこうした自然に存在する対称性の一つの発見であったと認識されている。その変換群は抽象的なローレンツ群であり、この群の座標という量についての特殊な表現が、運動座標系間の変換であるという見方になっている。

［佐藤文隆］

一般相対性理論

ニュートンの重力理論は相対性原理を満たしていないため、新しい重力理論が必要となった。アインシュタインは、慣性力と重力とは等価であるという実験事実に基づく等価原理を基礎として理論を組み立てた（図D）。重力は万有引力とよばれるように、すべての物体に平等に働き、同様に、加速度に質量を掛けた慣性力もやはりすべてに平等に働く。この事実を用いれば、慣性系に対して加速度運動をする座標系をとれば、つねに重力を打ち消して無重力にできる。そして、無重力系での物理法則をそれに対して加速度運動する座標系で記述するのが、一般相対性理論の数学的構造である。

　このように、慣性系でない一般座標系まで拡張して物理法則を表現するには、ミンコフスキー空間をリーマン空間に拡張しなければならない。リーマン空間の2点間の距離の2乗は
　　ds²＝g_μν(x)dx^μdx^ν　(6)
となる。ここでは計量テンソルg_μνは場所と時間の関数である。座標系を変換すれば他の物理量もg_μνも変換されるが、変換された新しい量の間には同じ関係が成立する。重力の作用は計量テンソルに表現されている。弱い重力の近似ではニュートンの重力ポテンシャル∅(x)は計量テンソルとg₀₀＝1－2∅(x)/c²のように関連している。このため重力がある場合には、このリーマン空間は一般には曲がった空間となる。

　計量テンソルを決める法則は、重力ポテンシャルを決めるポアソン方程式を一般化したアインシュタインの重力場方程式である。

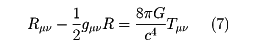
ここでR_μνはg_μνの二階微分を含むリッチ・テンソル、T_μνはエネルギー・テンソルである。Gはニュートンの重力定数で、この方程式は、エネルギーの分布によって四次元空間の計量テンソルが決まることを表している。時間・空間の構造は不動のものではなく物質の存在によって影響を受ける。このことはニュートンの絶対慣性系の考えを突き崩すものであり、19世紀末にマッハがニュートン力学の批判を通じて予言していたことであった。

　1917年、アインシュタインは物質密度が一様な静的宇宙モデルをつくるために、重力の引力に対抗する普遍的な斥力(せきりょく)を仮定する必要性に気づき、前記の方程式(7)を次のように拡張した。

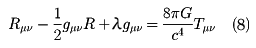
　アインシュタインは、宇宙は閉じた空間であると考え、全宇宙空間の大きさが上式のλ(ラムダ)で決まるとした。この意味でλを宇宙定数（宇宙項）とよんだ。しかし、その後1929年にアメリカの天文学者ハッブルによって宇宙膨張が観測的に検証されて、宇宙項はあってもよいが不可欠なものではなくなった。宇宙項はT_μνに組み入れて、真空のエネルギー密度と解釈できる。

　一方、1960年代の後半に、素粒子の場の量子論による統一理論の試みのなかで「真空」の新しい考え方が提案され、現在の標準理論もこの真空理論を基礎にしている。この理論では真空は何もないことではなく、ヒッグス場という真空場が有限であるということである。

　1980年代から、膨張宇宙の起源論として、大統一理論の真空場が宇宙項のように斥力に作用するとするインフレーション説の試みがなされてきた。また、超新星を標準光源とした距離測定法で、20世紀末には宇宙膨張が加速膨張であること、また2002年には宇宙マイクロ波背景観測衛星WMAPでの宇宙初期の密度ゆらぎの測定によっても、現在の加速膨張につながる宇宙のエネルギー密度で宇宙項に相当するダークエネルギーが卓越していることが確認された。ただし、このダークエネルギーの大きさは、存在がほぼ確かなヒッグス場や仮説的なインフレーション説の真空場の斥力の大きさより120桁以上小さいものであり、同質のものであるかどうかは明らかでない。

［佐藤文隆］

実験的検証

一般相対性理論が提唱された当時、その実験的検証とされたものは、次の三つであった。

(イ)スペクトル線の重力赤方偏移
(ロ)太陽重力での光径路の湾曲（図E）
(ハ)水星軌道の近日点の移動
　(イ)は、初め太陽や白色矮星(わいせい)で測られたが、1960年になって地上重力でのγ線に対する効果としても測られている。(ロ)は、1919年の日食の際に初めて観測され、この理論の真価を広く世界に知らしめた。1970年代に入って、クエーサーからの電波についてもこの効果が測られている。またクエーサーが手前にあるブラック・ホールのレンズ効果で二つに見える現象もこの効果の一つである。(ハ)は、19世紀の天体力学が指摘していた問題に解決を与えたものであった。1960年代から1970年代にかけてマリナー、バイキングなどの人工天体を用いて、この効果が測られた。

　1960年代に入って新しく加わった実験に
(ニ)レーダー・エコーの時間の遅れ
(ホ)人工衛星上のジャイロスコープの歳差運動
がある。(ニ)は、太陽近傍の空間が曲がっているため、そこを光が通過する時間が長くなる効果を測ったものである。(ホ)は、地球の自転に伴う新しい重力効果をみるものであるが、まだ検出に成功していない。

　これらは、すべて太陽系内の実験であったが、1974年に発見されたパルサーの二重星のシステムは、(ハ)、(ニ)の効果の他の天体での観測を可能にした。(ハ)は、水星では100年に43秒角と小さいが、パルサー二重星では1年に4度角と3万倍も大きい。

［佐藤文隆］

重力崩壊

一般相対性理論は、宇宙現象についても、いくつかの新しい事象を予言している。その一つは、星の進化の最終状態に現れる重力崩壊と、その結果として生ずるブラック・ホールの形成である。相対性理論の要請（公理）は、無限に固い物体の存在を否定する。このため、十分に重い天体はかならず収縮する。重力が強くなると、光でも捕捉(ほそく)されるようになり、星を形成するすべての物質は一点にまで圧縮されることになる。これを重力崩壊といい、途中で収縮を止めることはできないことが特異点定理で証明されている。

　重力崩壊の際には、大量の重力波がミリ秒程度の短い時間にバースト状に放出される。その結果として、最終的に実現する重力場の構造は非常に単純なものに落ち着くと考えられている。その構造は、特異点が事象の地平線に囲まれたブラック・ホールになるという推測である。この仮定を宇宙検閲仮説という。この仮定が正しいとすれば、ブラック・ホールの形態は質量と角運動量だけで完全に決まることになる。

［佐藤文隆］

ブラック・ホール

質量Mの物体が重力崩壊した場合、半径がr_g＝2GM/c²以下になると外から見えなくなり、半径r_gの表面で囲まれる内部からは光も物体もいっさい外に出られなくなる。ただしこの表面を通過して光や物体は吸収される。このように吸収する一方であるという性格を表現するため、ブラック・ホールの名称が1970年ころから用いられるようになった。また、このように内部からの情報を外に出さない限界の表面は事象の地平線（または地平面）とよばれる。地平線内には、すでに見た物体が落下していくが、地平線内に入ってしまうと、その物体でおこるできごと（事象）が見えなくなるという意味である。宇宙検閲仮説が正しければ、ブラック・ホールの時空構造はシュワルツシルト時空、回転のある場合はカー時空で与えられる。カー時空はシュワルツシルト時空を特殊な場合に含んでいる。事象の地平線をもつブラック・ホールは、カー時空が唯一であると考えられている。

　物理法則は、時間の反転に対して対称的であるので、吸収する一方のブラック・ホール解に対応して放出する一方のホワイト・ホール解も存在する。事象の地平線は今度はそこを通過して入れない面となる。ホワイト・ホールはそれをつくる過程がないため存在していないと考えられている。

［佐藤文隆］

宇宙の時空構造

宇宙全体の時間・空間構造も一般相対性理論により決定される。宇宙は時間的に拡大しつつある三次元の一様な曲率をもつ空間である。大域的にみて閉じた空間であるか否かは、ダイナミクス（動力学）だけからは決定できない。多連結の空間である可能性もある。また統一理論の観点から、宇宙空間を多次元空間の部分空間の面上に局限されているとみなす「ブレーンワールド（膜宇宙）」の考えも試みられている。

［佐藤文隆］

量子重力・統一理論

重力の量子効果は、プランク長さ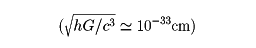

以下の超微視的世界で重要になる。この研究ではまたすべての相互作用の統一理論が試みられている。一般相対性理論は、この段階でより一般的な形の非量子論的な近似式であると考えられている。統一理論の試みでは多次元空間への拡張があり、それが四次元時空とコンパクトな内部空間に分離し、内部空間では素粒子相互作用の根拠となるゲージ対称性（ゲージ不変性ともいう。測定の基準を変えても物理法則が変わらないこと）が成立することとなる。また量子論を矛盾なく適用するために、空間は点の集合ではなく、超対称性をもつ二次元のひも（ストリング）の集合とみなす「超ひも理論（超弦理論もしくはスーパーストリング理論ともいう）」が展開されている。

［佐藤文隆］

『アインシュタイン著、矢野健太郎訳『相対論の意味』（1958・岩波書店）』▽『佐藤文隆、R・ルフィーニ著『ブラックホール――一般相対論と星の終末』（1976・中央公論社・自然選書）』▽『西尾成子編『アインシュタイン研究』（1977・中央公論社・自然選書）』▽『ウォルフガング・リンドラ著、小沢清智・熊野洋訳『特殊相対性理論』（1989・地人書館）』▽『S・ギビリスコ著、小島英夫訳『図説　アインシュタインの相対性理論――特殊および一般相対性理論と宇宙論』（1989・大竹出版）』▽『エル・ヤ・シュテインマン著、水戸厳訳『空間と時間の物理学』新装版（1989・東京図書）』▽『木村利栄・太田忠之著『古典および量子重力理論』（1989・マグロウヒル出版）』▽『冨田憲二著『相対性理論』（1990・丸善）』▽『アルバート・アインシュタイン著、金子務訳『特殊および一般相対性理論について』（1991・白揚社）』▽『マーティン・ガードナー著、金子務訳『相対性理論が驚異的によくわかる』改訂新版（1992・白揚社）』▽『砂川重信著『相対性理論の考え方』（1993・岩波書店）』▽『エルンスト・カッシーラー著、山本義隆訳・解説『アインシュタインの相対性理論』改訂新装版（1996・河出書房新社）』▽『松田卓也・二間瀬敏史著『なっとくする相対性理論』（1996・講談社）』▽『小玉英雄著『相対性理論』（1997・培風館）』▽『山下芳樹著『対話形式　相対論への探究――知的文化遺産として』（2000・コロナ社）』▽『佐藤文隆・小玉英雄著『一般相対性理論』（2000・岩波書店）』▽『窪田高弘・佐々木隆著『相対性理論』（2001・裳華房）』▽『講談社サイエンティフィク編、竹内薫著『ゼロから学ぶ相対性理論』（2001・講談社）』▽『恒岡美和著『明解　相対性理論入門――正しい理解を求めて』（2003・聖文新社）』▽『佐藤勝彦監修『図解　相対性理論がみるみるわかる本』（2003・PHP研究所）』▽『アインシュタイン、インフェルト著、石原純訳『物理学はいかに創られたか――初期の観念から相対性理論及び量子論への思想の発展』上下（岩波新書）』▽『内山龍雄著『相対性理論入門』（岩波新書）』▽『A・アインシュタイン著、内山龍雄訳『相対性理論』（岩波文庫）』

[参照項目] | アインシュタイン | 一般相対性理論 | 宇宙論 | 運動の法則 | 運動量 | エーテル | エネルギー | ガリレイ | ガリレイ変換 | 慣性 | 慣性系 | 近日点 | 空間 | クエーサー | ゲージ理論 | 原子核 | 光速度 | 座標系 | 時間 | 質量 | 重星 | 重力 | 重力波 | 重力場 | 赤方偏移 | 相互作用 | 素粒子 | 素粒子論 | 対称性 | 地動説 | 超ひも理論 | ディラック | 電磁気学 | 電磁場 | テンソル | 統一場理論 | 等速運動 | 特殊相対性理論 | ニュートン | 場 | バイキング計画 | 白色矮星 | ハッブル | パルサー | 万有引力 | ヒッグス粒子 | フィゾー | ブラック・ホール | ポアンカレ | ポテンシャル | ホワイト・ホール | マイケルソン | マイケルソン干渉計 | マイケルソン‐モーリーの実験 | マクスウェル | マッハ | マリナー計画 | ミンコフスキー | ミンコフスキーの時空世界 | モーリー | リーマン | リーマン幾何学 | ローレンツ | ローレンツ収縮 | ローレンツ変換

同時刻の相対性〔図A〕

双子のパラドックス〔図B〕

ミンコフスキー空間〔図C〕

等価原理〔図D〕

太陽重力での光経路の湾曲〔図E〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

相対性理論 (そうたいせいりろん)
theory of relativity

物理学は今世紀に入って相対性理論（相対論ともいう）と量子力学という二つの大きな飛躍を遂げている。これらはともに物理学の歴史の中でも最大級の革命であったのみならず，他の自然科学や哲学，さらにもっと広い文化の領域にまで計り知れない影響を及ぼした。しかし相対性理論と量子力学とは，その成立の過程において興味ある対照をなしている。量子力学が，多くの実験事実からいわば強制され，N.H.D.ボーアをはじめ多数の研究者の試行錯誤の結果，徐々に最終的な型に収束したのに対し，相対性理論はほとんどA.アインシュタイン1人によって完成され，しかももっぱらきわめて理論的な整合性を動機として作られた点に著しい特色がある。これがアインシュタインをして現代でももっとも魅力ある物理学者の一人たらしめている原因であろう。ここではまず座標変換，慣性系など，相対性理論の理解のための予備知識の説明から始め，次いで特殊相対性理論，一般相対性理論について概説したい。
→アインシュタイン

運動の相対性と座標変換

およそ運動とは，すべて，〈何か〉に対する運動として記述される。例えば川の水面を航行する船の速さという場合，岸に対する速さ，岸を走る自動車に対する速さ，水に対する速さ，さらには，すれちがう他の船に対する速さなど，いろいろなものが考えられる。これらは，それぞれ異なった意味と理由のもとに使われ，もちろんいろいろ違った値をとる。このような意味で運動は相対的であるといわれる。

　事情を数学的に正確に表すために座標系を導入する。上の例では，地上に固定した座標系で測った速度，自動車に固定した座標系に準拠した速度等々ということになる。速度だけではなく，場所を表す座標についても同様で，すべて座標系を指定して初めて定まるものであり，異なる座標系でみれば異なる値をもっている。

　再び船の例に戻って，川の水は岸に対して時速10km/hで流れているとしよう。これは岸に固定した座標系と，流れる水に固定した座標系との間の関係を与えている。もし船は下流に向かい，水に対して20km/hの速度で動いているならば，船の岸に対する速度は10＋20＝30km/hとなる。このような計算は速度の合成則と呼ばれるが，これはまた座標変換の一例でもある。つまり，二つの座標系の間の関係が与えられているとき，一つの座標系における速度から，もう一つの座標系における速度が定められる。

　ここで述べた座標変換，あるいは速度の合成則はわれわれの日常的な経験，常識に一致するものであるが，このような常識は，光の運動についてはまったくあてはまらないことが判明した。この困難を解決するためにいろいろな考え方が提出されたが，最終的な解決は1905年，アインシュタインによって発表された特殊相対性理論によって与えられた。この理論は，時間と空間に関する従来の考え方を根本的に変えることを要求しており，その結果として，時計のおくれ（あるいは双子のパラドックス），質量がエネルギーをもつことなど，おどろくべき結果を多数予言した。それらはいずれも直接，あるいは間接に検証され，とくに，光速に近い速さで運動する素粒子の研究には，理論，実験をとわず，特殊相対性理論を駆使することが必要不可欠となっている。

　特殊相対性理論が特殊と呼ばれるのは，考慮する座標変換が慣性系どうしの間のものに限られているからであるが，もっと一般的な座標変換まで取り扱う理論は15年になって発表され，一般相対性理論と名付けられた。これは，特殊相対性理論よりもさらに革新的な内容を含む重力の理論となるのであるが，この間の事情を理解する手始めとして，ニュートンの力学における慣性系に関して説明しておかなければならない。

慣性系

慣性系とは，ニュートンの運動法則が成り立つ座標系のことである。地上に固定した座標系は近似的に慣性系である。実際，摩擦のない水平な台の上におかれた物体は，力を加えなければ静止したままか，または等速直線運動を続ける。すなわち，ニュートンの第1法則（慣性の法則）が成り立っている。これに反して加速中の乗物の中では，うしろに引かれるような仮想的な力が働き，また回転する円板の上では同じように仮想的な力である遠心力が働く。これらは慣性力と呼ばれ，このような真の力でないものを加えなければならない点で，加速中の乗物や，回転する円板に固定した座標系は慣性系ではない。また，地上に固定した座標系が近似的にしか慣性系でないといったのは，地球は慣性系に対して自転による回転をしており，地球上の物体は，そのための遠心力やコリオリの力を受けている証拠があるからである。

　ともかく，x，y，zの直交座標をもつ一つの慣性系があり，それをSと記そう。Sのx軸，y軸，z軸と互いに平行なx′，y′，z′の座標軸をもち，Sに対してx軸方向に一定の速度vで動いている座標系をS′とする。原点が一致した時刻をt＝0，t′＝0とすると，両者の座標には，

　x′＝x－vt，y′＝y，z′＝z ……（1）

という関係がある。これは一種の座標変換であり，ガリレイ変換と呼ばれる。この変換によって物体の速度のx，y，z方向の成分（V_x，V_y，V_z）はそれぞれ，

　V_x′＝V_x－v，V_y′＝V_y，V_z′＝V_z　　　……（2）　

のように変換される。これが速度の合成則であることは，先にあげた船の例からすぐに理解されるであろう。

　ところで，このガリレイ変換によって物体の加速度は不変に保たれる。なぜならば，速度は（2）に従って変わるが，それは単に速度の目盛の原点をずらせただけであり，速度の変化率の値は変わらないからである。とくにSでみて等速度運動は，S′でみても等速度運動であり，Sで慣性の法則が成り立っているならば，それはS′でも同様に成り立っていることになる。したがって，一つの慣性系からガリレイ変換によって移る座標系はすべて慣性系である。vの値はどんなものでもよいのであるから，慣性系は無数に存在する。これらの慣性系は，運動法則に関する限りどれも互いに同等であり，どれかが他に対して特別に優位に立つことはない。このことはガリレイの相対性とも呼ばれる。

　しかし慣性系は全体として，他の座標系（非慣性系）に対して特別の地位を保っている。つまり，真の力のみを考慮に入れてニュートンの運動法則がそのまま成り立つのは，慣性系に限られるのである。ニュートンは慣性系（の全体）を，ある意味で絶対座標系であると考えていた。しかしE.マッハはこの考えに反対し，宇宙の恒星系全体に固定された座標系（およびこれからガリレイ変換によって移ることのできるすべての座標系）が慣性系であるとした。この背後にあるのは，慣性系は全宇宙の物質の分布のしかたによって自然に決まるものであるという考え方であり，いわば絶対性の排除，相対性の主張ということもできる。マッハの原理と呼ばれるこの考え方は，多分に哲学的なものであったが，絶対座標系の否定という点を通じてアインシュタインに強い影響を与えたといわれる。完成された一般相対性理論において，慣性系がどのような位置を占めるようになったかについては後に触れる。

特殊相対性理論special theory of relativity

1864年に定成されたマクスウェルの電磁理論からは，真空中をc≒3×10⁸m/sで伝わる波動の存在が予言され，電磁波と名付けられた。この伝搬速度は，すでに測定されていた光の速度とよく一致し，ここに，光の本性は電磁波であるという考えが生まれたのである（光の電磁波説の確固たる基礎は1888年H.R.ヘルツによって与えられ，その実験はヘルツの実験と呼ばれている）。しかし，上記の3×10⁸m/sという速度は，何に対する速度であろうか。空気中を伝わる音波の場合ならば事情は簡単である。すなわち，音速（≒340m/s）とは，媒質である空気に対する速度である。しかし，マクスウェルの方程式から電磁波の存在を導くに際しては何も媒質は仮定されてはいない。すなわち，電磁波は真空を伝わるものとしてその存在が導かれたのであるが，真空に座標系を固定するわけにはいかない。これはあまりに明白な理論的困難である。一方，速度の異なる座標系で光速を測定し，果たして差が現れるかどうかをみようとする実験も行われた（マイケルソン=モーリーの実験）が，そのような光速の差を検出することはできなかった。これは，（2）式の速度の合成則が成り立っていないことを意味するものであり，深刻な困難であった。

　ところで，この当時，広く行われた議論にエーテル説なるものがあった。それは，電磁波は真空や物質の中を一様に満たしているエーテルという仮想的な媒質の中を伝わるというものであり，マイケルソン=モーリーの実験（これも静止したエーテルの存在を実験的に見いだそうとしたものである）が，これに対して否定的な結果を与えた後も，この考えはなかなか捨てられなかった。このような仮想的な物質を仮定することは，かえって困難を増すのみであったが，H.ローレンツとG.フィッツジェラルドは，それぞれ独立に，エーテル説に立ったうえで，マイケルソン=モーリーの否定的実験を説明するためには，速度vで動く物体は，その進行方向に倍短くなると考えればよいことを示した（ローレンツ収縮）。しかし，あらゆる物体が，その種類をとわず一様に収縮する機構を説明することはできなかった。

アインシュタインの出発点

このような状況の中で，アインシュタインが提出した考えは次のようなものであった。ただし，彼自身はマイケルソン=モーリーの実験を説明しようとしたのではない。マクスウェルの電磁理論と力学の法則との整合性が問題なのであった。彼はまず，光の速度はどんな慣性系からみても同じであることを認めることから出発しようという（光速度不変の原理）。これが素朴な速度の合成則（2）とどんなに矛盾しようとも，一方において真空中におけるマクスウェル理論を正しいものと受けいれる限り，これ以外に考えようはないといわば居直った形である。考え直さなければならないのは，むしろ，それまで何の疑いももたれなかった速度の合成則のほうではなかろうかというのである。これはまた，慣性系の間の座標変換としてのガリレイ変換（1）も改変されるべきであることを意味する。

　正しい座標変換としてアインシュタインが（1）式に代わるものとして提出したのは，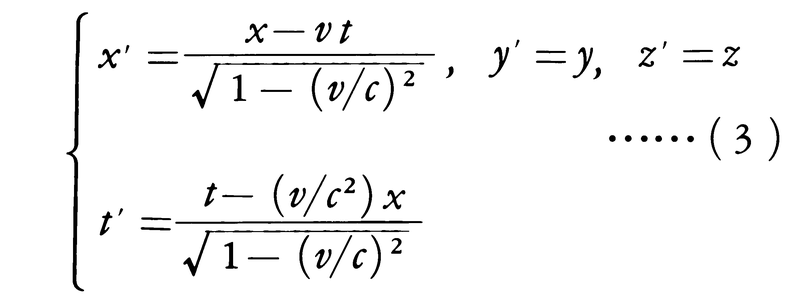

である。この変換式はローレンツ変換と呼ばれ，ローレンツがローレンツ収縮を導いた際に用いたものと同じ形であるが，その前提はまったく異なる（この式の導き方については，コラム〈ローレンツ変換の導き方〉を参照）。

　この変換式が示すもっとも著しい特徴は，空間と時間（xとt）とが互いに移り変わることである。以前の考え方では，時間はあらゆる座標系に共通な流れであり，どんな座標変換を行っても絶対不変に保たれるものと考えられていた。すなわちt′＝tであると，暗黙のうちに仮定されていたのである。このあまりにも明白とされてきた常識を打破することが，光速にまつわるなぞを完全に解き明かす鍵であった。

同時刻の相対性

（3）式が意味する物理的内容について，アインシュタインは多くの思考実験を用いて説明している。その代表的なものとして，ここでは同時刻の相対性をとり上げてみよう。

　もし時間があらゆる座標系に共通なものであれば，二つの事象が同時に起こるということは，どの座標系にとっても共通な事実である。しかしこれは光速度不変の原理とは両立しないことを以下に示そう。そもそも離れた2点における同時刻とは，どんな物理的操作によって確認されるかをアインシュタインは考察する。一つの典型的な方法は両地点の中間点で光を発し，それが両地点で受けとられる時刻が同時刻であるとみなすことである。

　例えば電車の中央Cから発せられた光が，前後に等距離ずつ進んで，先端A，後端Bに達するとしよう。電車に固定した座標系Sでみれば，光は，上に述べた意味で同時にA，Bに達する。一方，この一連の過程を，地上に固定した座標系S′でみてみよう。Cを発した光は，光速度不変の原理により，S′でみても同じ速度cで進む。したがってCが光を発した瞬間に，Cと同じ場所にあった地上の点C′が光を発射したのと同じことである。さて，地上からみていると，電車の後端BはC′に近づきつつあり，一方，先端AはC′から遠ざかりつつある。ゆえに前向きの光がAに追いつくより以前に，後ろ向きの光はBに出合ってしまう。つまり，Sで同時刻と認める二つの事象は，S′では同時刻とは認められない。この思考実験が示すように，光速度不変の原理を認める限り，同時刻という概念には絶対的な意味はなく，座標系によって異なる相対的な意味しかもたないことがわかる。さらに考察を進めると，自分に対して動いている相手の座標系の時計は進み方が遅れ，また物体の長さは縮んでみえるという驚くべき結論に達する。この長さの縮みは，実は以前ローレンツが，マイケルソン=モーリーの実験を説明するために仮定したもの（ローレンツ収縮）と結果においてまったく同じものであるが，アインシュタインは新しい考え方に基づいて，これに自然な解釈を与えたものということができる。

時空

（3）式が示すように，ある座標系で時間と考えている量が，他の座標系でみると，時間と空間座標のまじり合ったものになるというのであるから，時間と空間の間にはもはや絶対的な区別はつけられない。むしろ両者を統一した時間・空間，または略して時空こそが物理的記述の枠組となるべきである。この考え方はH.ミンコフスキーによって数学的に整備され，四次元ミンコフスキー時空という，擬ユークリッド空間の概念を生み出したのである。

　前に，ニュートンの力学に関するガリレイの相対性について述べたが，これはアインシュタインの特殊相対性原理に昇格される。すなわち，ローレンツ変換によって移ることのできる慣性系は，どれも互いに同等であり，物理法則は，どの慣性系においてもまったく同じ表現で記述される。このような法則の不変性，または共変性を数学的に定式化するには，ミンコフスキー時空における幾何学的方法を用いるのがとくに便利である。

理論からの帰結と発展

ローレンツ変換（3）からは，さまざまの新しい結果が導かれるが，速度の合成則も（2）式ではなく，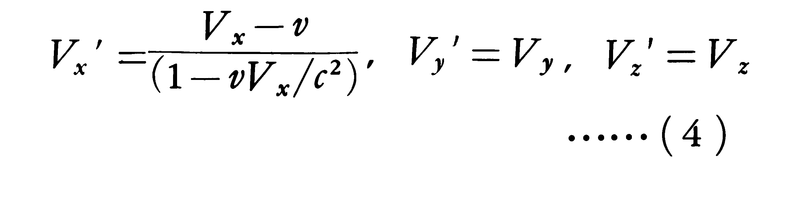

となる。この式によると，光速以下の速度をどれだけ合成しても決して光速をこえないことがわかる。つまり光速cは，現実に達成しうる速度としては最大のものである。また特別の場合としてV_x＝cとおくとV_x′＝cとなり，もくろみどおり，光速度不変の原理に一致するようになっている。

　一方，速度vがcに比べて小さい極限では，（3）式は（1）式のガリレイ変換に移行する。これにより，ニュートンの力学は，運動速度が光速に対して十分小さい場合の近似法則であり，通常の経験で，先に述べた同時刻の相対性のような奇妙な現象がみられない理由も理解される。反対に速度が光速に近くなれば，ニュートンの運動方程式は大幅に変更されなければならない。その一つの現れは，質量mの質点が速度Vで動いているときの運動エネルギーEを表す式，

にみられる。この式でVを0にしてもエネルギーは0にならず，E＝mc²となる。質量は，それが静止しているだけでmc²のエネルギーをもつのである。これが有名な質量とエネルギーの等価性であり，後に原子核エネルギーとして利用される巨大なエネルギーの理論的基礎である。

　ニュートン力学はこのように修正されたのであるが，マクスウェル理論のほうはどうなったのであろうか。実は，アインシュタインが初めから予期したとおり，電磁気学の法則は，そのままで特殊相対性理論に矛盾なく作られていたのである。つまり，ニュートン力学とマクスウェル理論との衝突は，後者を尊重する形で収拾されたのである。

　特殊相対性理論の発展の一つとして，量子力学との結合をあげておかなければならない。現在の素粒子論の基礎となっているのは，特殊相対論的場の量子論であるが，これによれば，一つの素粒子に対応する場は，ローレンツ変換に対する既約表現とみなされる。この理論は，ディラックの電子論（ディラック方程式），湯川秀樹の中間子論などを経て量子電磁力学，弱い相互作用の理論など，輝かしい成功をもたらしたが，一方，いわゆる発散の困難をも引き起こしている。これは局所的な場の性質が，特殊相対性理論の枠組の中できびしく制約されていることに原因がある。それにもかかわらず，この理論を離れて現在の素粒子物理を考えることはほとんど不可能といえよう。

一般相対性理論general theory of relativity

ローレンツ変換よりも一般的な座標変換（これを一般座標変換と呼ぶ）を考えると，必然的に重力の問題にかかわることになる。その理由は，非慣性系では慣性力が現れるが，これは，次に述べる等価原理のために重力とまったく同じ性質をもつことにある。

等価原理principle of equivalence

ニュートンの力学には2種類の質量が登場する。第1は慣性質量m_Iで，運動方程式，

　m_Iα＝f　　　……（6）　

の左辺に現れ，慣性の大小を表すものであって重力とは直接の関係がない（αは加速度，fは力）。（5）式を地球表面近くにおける物体の落下運動にあてはめてみよう。右辺の力fは，物体が万有引力によって地球に引かれるために生ずる重力である。地球の全質量Mは中心に集中したと考えてよい。そうすると質量m_Gの物体との間には，

という万有引力が働く。ここでrは地球中心までの距離，Gは万有引力定数である。この質量m_Gは重力の強さを表し，物体の慣性とは本来無関係のものである。その意味で，（7）式に現れるm_Gは重力質量と呼ばれる。さて（7）式を（6）式の右辺に代入すると，加速度αはm_G/m_Iという比に比例することがわかる。一方，ガリレイの伝説的なピサの斜塔での実験以来，物体の落下の加速度はどんな物体についても等しい値をもつことが知られている。このことから，比m_G/m_Iは物体の種類によらないこと，したがって2種類の質量は互いに比例していることが結論される。質量の単位を適当に選べば，両者はまったく同じものと考えてよい。概念としてまったく異なる量が互いに一致するのはなぜかについて，ニュートンは答えていない。何か別の原理の存在が予想される。アインシュタインは，これを等価原理と呼んで，重力のもつ重要な特徴と考えた。

　さて慣性力は，慣性質量に比例している。もし等価原理が正しいとすると，これは重力質量に比例するはずで，したがって慣性力は，万有引力から生ずる真の重力と等価なものと考えざるを得ない。この事情を説明するためにアインシュタインはエレベーターの例を引合いに出す。

　いまエレベーターが急に上方に引き上げられたとしよう。中の人間は，急に強い力で床におしつけられるように感ずる。これについて二つの解釈が可能である。第1は，近似的な慣性系である地球に対して加速度運動をする非慣性系にいるために，慣性力が働いたと考えることである。第2は，地球の質量が急に増したために，真の重力が大きくなったと考えることである。常識的には前者をとるのであるが，外を見ることのできない内部の人間にとって，後者を否定することは原理的に不可能である。なぜならば，重さが増える割合はエレベーター内のあらゆる物体についてまったく同様だからである。これはまさに等価原理のせいである。

　もし逆にエレベーター（または宇宙船）が自由落下を始めたとすると，いわゆる無重力状態となる。すなわち，慣性力という仮想的な力が真の重力をちょうど打ち消し，初めから真の重力がまったくないのと同じ効果をもたらすのである。このような考察を一般化すると，重力は座標変換によってどんな値にすることもでき，とくに重力を完全に消し去ることもできるということができる。これは，先に述べた単純な等価原理，つまり慣性質量と重力質量の等価性よりもさらに一般的な等価原理の表現であり，これをアインシュタインは一般相対性理論を作る際の物理的な柱とした。

リーマン幾何学と一般相対性理論

次にもう少し数学的な面に移ろう。特殊相対性理論で考える時空はミンコフスキー空間であった。これは直交空間ではないが，やはり直線座標で表すことのできる，いわば平らな空間である。しかし慣性系から，それに対して加速度運動をしている座標系に座標変換すると，当然曲線座標系になる。このような曲がった空間を記述するためにアインシュタインはリーマンの幾何学を採用した。ところで上に述べた等価原理によって，非慣性系では重力が存在するのであるから，重力は時空の曲がりにほかならないということになる。逆に重力があれば時空は曲がり，四次元のリーマン空間になると考える。

　このリーマン幾何学のことばで等価原理を表すと次のようになる。四次元リーマン時空の各点で接空間が定義され，それはミンコフスキー時空である。つまり，適当な座標変換によってつねに無重力状態を作ることができ，それに対しては特殊相対性理論が成り立つということを要請するのである。この接空間がアインシュタインの考える慣性系である。これは各時空点ごとに別々に定義されるもので，局所慣性系とも呼ばれ，ニュートンやマッハの考えた大域的な慣性系とはかなり異なったものとなる。

理論の展開

このように，曲がった時空と等価原理という基本仮定のうえに立って，理論はリーマン幾何学の処方に従って展開される。その詳細は省略するが，主要な内容を2点にまとめてみよう。

（1）リーマン幾何学のもっとも基本的な量は計量テンソルである。時空が平らなミンコフスキー空間であるとき，計量テンソルは対角的な定数となる。これからのずれが重力を表す。重力のために曲がった時空の中で質点は（他の力がなければ）測地線に沿って動く。測地線とは，2点を結ぶ最短の曲線で，球面の例でいえば大円がこれである。これは，平らな空間における直線の概念の自然な拡張である。この型の質点の運動法則はニュートンの第1法則，つまり力を受けていない質点は直線上を等速度で動くという法則の拡張となっており，そこには慣性質量も重力質量も現れない（第2法則に相当するものは，重力に関する限り登場しない）。この意味で，もっとも単純な等価原理は自動的に導かれるのである。さらに詳しい分析により，計量テンソルが，ニュートンの力学に現れる重力ポテンシャルを拡張したものとなっていることがわかる。

（2）ニュートンの万有引力の法則は，質量が存在すると，そのまわりに重力場ができることを示している。数学的にいうと，重力ポテンシャルはポアソン方程式の解であり，ポテンシャルの源は質量分布である。このような重力場の方程式の拡張が，アインシュタイン方程式と呼ばれるものである。これは計量テンソルに関する2階偏微分方程式で，その源はエネルギー・運動量テンソルである。

　以上の理論にきわめて特徴的なことは，計量テンソル，したがって時空の構造自身，物質の存在のしかたによって規定されることである。一方，物質の運動は時空の曲り方，つまり重力によって支配されるのであるから，物質分布と時空の構造とは互いに影響を与え合う力学的な量であると考えられる。これは特殊相対性理論を含めて旧来の，時空は物質の運動を記述する枠組としてあらかじめ与えられているものという概念を打ち破る，真に画期的な考え方であった。

理論の検証

次にこの理論を検証するために，アインシュタイン自身が提唱した三つの実験について述べよう。ふつうの状況では重力はあまり強くなく，ニュートン力学からのずれはきわめて小さいので，その検出は容易でない。

（1）重力赤方偏移　曲がった時空における光の伝搬を考察することにより，強い重力場の中で発せられた光が重力場の弱い場所にくると振動数が減少することがわかる。アインシュタインは太陽からくる光にこの効果が現れ，スペクトルが赤いほうへずれること（赤方偏移）を予想した。しかしこれは，コロナ，その他の雑音によってかくされてしまうことがわかった。1960年になってR.V.パウンドらは，放射性同位元素からのγ線の放出，吸収を調べ，理論値と1%の精度で一致する結果を得た。この際にはメスバウアー効果を用いた超精密測定が決定的な役割を果たした。

（2）太陽による光の湾曲　質点の運動の軌道である測地線は，先に述べたように質量に無関係である。したがって質量が0の光も測地線に沿って動く。つまり光も重力場の影響で曲がると期待される。この効果も非常に小さいので，なるべく強い重力場，したがって大きな質量による重力場に注目しなければならない。そのためには太陽が最適である。しかも太陽のすぐそばを通る光がよい。そこで皆既日食の際の太陽の近くに見える星を観測することが計画された。

　最初の観測は第1次世界大戦の直後1919年，イギリスのA.S.エディントンによって試みられ，学会のみならず一般社会にも大きな反響を呼んだ。その後も観測が繰り返されたが，70年には準星の出す電波の干渉を用いて同種の測定が行われ，初めて10%の精度で理論値との一致が得られた。

（3）水星の近日点移動　純粋な万有引力のもとでは，太陽のまわりの惑星の軌道は楕円であり（ケプラーの第1法則），その長軸，短軸は恒星系（慣性系）に対して一定の方向を向いている。しかし一般相対性理論によって同じ問題を扱うとこれからのずれが生じ，それは近日点の移動として観測されるはずである。実際には，この種の移動は他の惑星の影響などによっても生じ，既知の原因によっては説明されないごくわずかの不一致が残っていた。太陽にもっとも近い水星の場合，100年につき43″がそれであった。アインシュタインはみずからの計算によって，このずれが完全に説明できることを見いだした。彼はこの成功によって，自身の理論に確信をもったといわれている。

研究の現状

最後に，一般相対性理論の研究の現状について簡単に述べておく。

（1）実験的研究　太陽の向こう側にいる水星に向かって電波を送ってその反射を受け，電波が太陽の近くを通る際に生ずる時間の遅れを測定するレーダー・エコーの実験が1970年に行われ，一般相対性理論の第4の実験的検証となった。人工衛星を使った同種の大規模精密実験も行われている。また今後の天体，測地測定には，一般相対性理論による補正もとり入れられる計画である。もう一つの方向として，アインシュタイン方程式の解として存在が期待されている重力波を実際に検出しようとする試みが精力的に行われている。

（2）アインシュタイン方程式の厳密解　この非線形方程式の解法は容易ではないが，1916年，K.シュワルツシルトによって最初のものが得られた。その後，H.ワイル，R.P.カー，富松彰・佐藤文隆などの解が見いだされ，さらに数学的な進歩が著しい。また数値解法の研究も進んでいる。

（3）天体物理学における応用　この分野でもっとも注目を集めているのは，電波，あるいはX線天文学によってブラックホールと思われる天体が発見されていることであろう。ブラックホールとは，上に述べたシュワルツシルトの解が示す，極端に強い重力場がもつ奇妙な領域のことで，中性子星の重力崩壊によって実現されると考えられている。一般相対性理論は，重力場が弱い極限でニュートンの理論に一致するように作られているが，その反対の極限の代表的な例がブラックホールであり，その意味で一般相対性理論の真価を示す現象といえよう。

（4）宇宙論への応用　アインシュタイン自身は，シュワルツシルトの解で与えられるような強い重力場にはあまり関心をもっていなかったということであるが，別の意味で重力場が支配的な役割を演ずる宇宙論には早くから取り組んでいた。現在の膨張宇宙論は，22年，A.フリードマンによって得られたアインシュタイン方程式の解を基礎とする方法によって定式化されるのがふつうである。この考え方によれば，われわれの宇宙は100億～200億年前に，小さな1点から出発して膨張してきたものとみなされ（火の玉宇宙論），その間，素粒子や原子核，また銀河や星がどのようにして形成されてきたかについて詳しい分析が進められている。

（5）統一理論　一般相対性理論においては，重力場は時空の幾何学的性質に起因するものとされるが，もう一つの物理的に重要な場である電磁場にはそのような背景がない。ワイルは，リーマン幾何学を拡張し，電磁場もまた幾何学的起源をもつような時空の理論を展開した（1918）。このような考え方は統一理論（統一場理論）とも呼ばれ，後にアインシュタインも熱心に追究した。現在では，各種の素粒子の場との統一を目ざす理論についての研究が活発である。その際に有力な武器となっているのが，ワイルによって提唱されたゲージ原理である。これに伴って，重力場の量子論についても研究されている。

　さらに最近の発展として，素粒子の弱い相互作用，電磁相互作用と強い相互作用を統一する大統一理論が議論の対象となっているが，この理論の真に特徴的な様相は，膨張宇宙の非常に初期の段階で実現されていたと考えられ，この点からも，素粒子物理学と重力との統一的記述が現実的課題となりつつある。
執筆者：藤井 保憲

哲学的意義

哲学との関連で，相対性理論のもつ意義およびそれのもたらした影響について付言しておこう。まず，存在論に即していえば，相対性理論は〈関係主義的（非実体主義的）〉な存在観を促すゆえんとなった。哲学においては，19世紀のある時期からヨーロッパにあってすらさすがに関係主義的な存在観が登場するようになっていたが，科学的世界観の拠点をなす物理学においては，古典物理学的実体主義が牢固（ろうこ）として支配していたため，非実体主義＝関係主義の貫徹が阻まれていた。この際，実体主義というのは世界が〈実体〉（ens per sui，つまり，対他的関係とは無関係に独立自存するもの）からなっているとみる存在了解の謂（いい）であるが，相対性理論は古典物理学的世界像において，〈対他的関係とは無関係に独立自存する究極的存在〉とみなされていた〈絶対時間〉〈絶対空間〉〈質量〉といったものの実体的自存性を否認し，これら物理の基本的存在ですら相互浸透的，相互規定的な関係的存在態であることを明らかにした（時間と空間との相互浸透的規定関係，一般相対論における時空間と質量との相互規定的関係などを想起されたい）。このことが，量子力学の知見とあいまつことによって，物理的実体主義からの解放，関係主義的存在観の確立を促すものとなった。

　次に，認識論に即していえば，相対性理論は〈間主観的構成主義intersubjektiver Konstruktionismus〉の認識観を促すゆえんとなった。相対性理論以前の科学観においては，〈対象的事実〉は認識主観とは無関係に独立自存するものと思念されていたが，相対性理論は上述のように，〈同時刻の相対性〉をはじめ，〈空間の収縮〉や〈時間の伸長〉など，対象的事実が観測系と相対的であることを自覚せしめた。観測問題が物理そのものの場面で深刻化するのは量子力学をまってではあるが，認識論的にみれば，相対性理論においてもすでに，〈同一与件〉に関する相異なる観測系での相異なる観測現相を，間主観的な統一相で定式化した〈所知態〉がいわゆる対象的事実にほかならないという構制になっている。このことの自覚に伴って，〈対象的事実〉とは間主観的に統一的に妥当する相に構成された所知態であるという事実観，認識観が促され，伝統的な模写説的認識観がカント主義的な先験的構成主義とは別の論脈においてしりぞけられることになった。

　相対性理論は，存在論とか認識論とかに限定できない部面でも，哲学界，思想界に巨大な影響を及ぼしており，物理学における革新的な理論という域をこえて，画期的な知的遺産であるといえよう。
執筆者：廣松 渉

コラム－ローレンツ変換の導き方

コラム－双子のパラドックス

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

相対性理論【そうたいせいりろん】

1905年以来アインシュタインによって展開された物理学の理論体系。相対論とも。ニュートン力学の絶対空間・絶対時間（時間）の考えを否定し〈物理法則はあらゆる座標系に対し同じ形式で表される〉という〈相対性原理〉を基本要請とする。相対性原理を互いに等速直線運動をする座標系に適用したのが特殊相対性理論，互いに加速度運動をする一般の座標系に拡張したのが一般相対性理論。
→関連項目カルタン｜空間（哲学）｜古典物理学｜シンクロサイクロトロン｜ホーキング｜矢野健太郎｜四次元世界

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

相対性理論
そうたいせいりろん
relativity theory

相対論ともいう。ある範囲の座標系がすべて物理的に同等であって，これらのどの座標系でも物理法則はまったく同形でなければならないという要請を相対性原理という。相対性原理の要請を満たす物理理論を相対性理論という。ニュートン力学はガリレイの相対性原理を満たし，すべての慣性系を同等とみなす相対性理論である。しかし，これを除外して，普通は相対性理論といえば A.アインシュタインが提唱した特殊相対性理論，一般相対性理論，統一場理論をさす。なお，単に相対性理論というときは特殊相対性理論をさすことが多い。

出典　ブリタニカ国際大百科事典 小項目事典

山川 世界史小辞典 改訂新版

相対性理論(そうたいせいりろん)
theory of relativity

アインシュタインによって提唱された物理学理論。特殊(1905年)および一般相対性理論(16年)がある。特殊相対性理論は質量とエネルギーの関係公式(「E＝mc²」，光速の近くでは時間がゆっくりになる)で広く知られる。一般相対性理論は時間，空間，物質を対象とする壮大な学説で，1919年の日食の際に太陽近くでスペクトル線の屈折(重力赤方偏移)を観測，確認された。宇宙の誕生，発展，消滅(ブラックホール)を予測，説明する量子力学の理論的基礎となる。

出典　山川出版社「山川 世界史小辞典 改訂新版」

旺文社世界史事典 三訂版

相対性理論
そうたいせいりろん
theory of relativity

アインシュタインが相対性原理を前提に展開した理論
1905年に発表した特殊相対性理論と1914〜16年に完成させた一般相対性理論とからなり，ふつう前者をさす。たがいに等速度で動いているふたりの観測者がみると，物理法則は同じ形で表されるという原理。

出典　旺文社世界史事典 三訂版

世界大百科事典（旧版）内の相対性理論の言及

【アインシュタイン】より

…そこに7年間勤めたが，しごとの合間に行った理論物理学の研究は，20世紀物理学の基礎を築くことになった。すでに1901年から熱力学および統計力学に関する論文を発表していたが，05年に光量子仮説，ブラウン運動の理論，特殊相対性理論という，根本的かつ革命的理論を立続けに提出したのである。そのため，この年は〈奇跡の年〉といわれる。…

【宇宙】より

…天体に関する具体的知識はほとんど皆無であったものが，1838年に恒星の距離が測定され，19世紀後半には太陽や恒星，星雲の分光観測が進んで天体の物理･化学的な理解が増した。20世紀に入ると量子力学と相対性理論の二つの新しい物理学が興り，量子力学は天体からの光を解明する理論的手段を与え，1920年代から本格的な天体物理学が進展し，観測の発展と相まって太陽や恒星，星間物質や星間雲，星団や星雲に関する本質的な知識が得られるようになった。また原子核やその反応についての実験や量子力学的研究が進んだ結果，ベーテH.A.Bethe(1906‐　)とワイツゼッカーC.F.von Weizsäcker(1912‐　)により恒星中心部における原子核反応が具体的に明らかにされ(1938‐39)，太陽をはじめとする恒星のエネルギー源を説明するとともに，恒星進化および宇宙の物質進化の研究が可能になった。…

【空間】より

…このことがのちに20世紀に入ってもう一つの空間概念の大きな変革を支えることになった。アインシュタインの手で生まれた相対性理論は，時間と空間との間のカテゴリカルな区別を取り除いたという意味で，やはり西欧的空間(時間)概念の歴史にとっては画期的なことだったといってよい。時間と空間は，独立の概念ではなくなり，相互に浸透し合った一つの連続体として理解されることになったからである。…

【時間】より

…　このように，近代西欧哲学のなかでは，時間は，世界の存在の形式か，世界の存在を支える枠組みか，人間の認識の形式か，いずれにしても人間のいきいきとした〈生〉そのものとは無関係な広域的概念になりつつあったが，それを人間の生の様式へ引き戻そうとしたのが，19世紀末以降のベルグソンによる〈持続〉やフッサール，ハイデッガー，サルトルらの現象学的な〈時間性〉の提案だった。さらに20世紀初頭における相対性理論と量子力学の誕生は，時間概念に決定的な新しい展開を与えた。相対性理論では，絶対時間や絶対的同時性が成立しないことが明らかになった(そこから〈双子のパラドックス〉が生まれる)ばかりではなく，それまで空間と別個の座標軸を与えられていた時間が，空間と独立に扱われるべきでないという新しい事態を迎えたし，量子力学では，エネルギーとペアとなって非可換な2量を構成する時間(物理的観測量としての)が，ハイゼンベルクの不確定性原理を満足すべきものであることが明らかにされ，そこから，一種の〈多時間〉的な発想も生じた。…

【マッハ】より

…彼の研究関心は一種のルネサンス人と形容しうるほど多岐にわたっており，物理学，哲学，科学史，心理学，生理学，音楽論の各分野で第一級の業績を残している。物理学では超音速の先駆的研究によって速度単位マッハ数にその名をとどめ，また〈マッハの原理〉は一般相対性理論への道を開くものであった。心理学における〈マッハの帯〉や〈マッハ効果〉の発見，生理学における〈マッハ=ブロイアー説〉など彼の名を冠する業績は数多い。…

※「相対性理論」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」