精選版 日本国語大辞典 「算術」の意味・読み・例文・類語
さん‐じゅつ【算術】
- 〘 名詞 〙
- ① 計算の方法。古くは数学全般と同義。
- [初出の実例]「筭博士二人。〈掌レ教二筭術一〉」(出典:令義解(718)職員)
- [その他の文献]〔漢書‐律歴志〕
- ② 算木による占い、まじない。
- [初出の実例]「併良明加持、彼僧筭術効験歟。可レ貴可レ喜」(出典:看聞御記‐応永二四年(1417)五月二三日)
- ③ 初等数学のこと。記数法、正の整数、小数、分数の四則計算、比例、量の計算などを取り扱う。小学校および中学校初学年で教えた。〔英和対訳袖珍辞書(1862)〕
- ④ 小学校の旧教科名。現在の算数にあたる。
- [初出の実例]「小学にては句読筆道、筭術(サンジュツ)の三科に分ち」(出典:新聞雑誌‐五号・明治四年(1871)六月)
改訂新版 世界大百科事典 「算術」の意味・わかりやすい解説
算術 (さんじゅつ)
もとの意味は文字どおり算(かぞ)える手段ということで,古い用例には古代中国の数学書《九章算術》がある。和算において術という言葉を使うのは,特殊な手法を指すのがふつうである。例えば関孝和の角術というのは,正多角形の一辺を与えて,内接円および外接円の半径を求める公式である。明治になって算術という言葉が再登場し,やがて小学校で教える初等数学の教科名として採用された。そのため,算術というのは,そのような初等数学を意味することが多い。一方,arithmetic(原義は数えること)の訳語として算術という言葉を用いることがある。arithmeticという語は原義よりずっと広い意味に用いられるので,算術何々という形の語の算術は,算術級数は等差級数,算術平均は相加平均というように,初等数学とはだいぶ異なる意味をもつ。
初等数学としての算術の内容については,四則演算(加減乗除)の範囲で,方程式を用いることなく解ける問題を扱うものと考えるのが適当である。したがって,一次方程式,連立一次方程式を利用すれば容易に解けるものが多い。《九章算術》は方程式も利用したが,数学書である以上当然といえよう。われわれが通常算術というとき,原義よりだいぶ狭く解釈しているともいえる。初等数学において学童が出会う初期の難事は九九を覚えることであるが,この九九の語は,古代中国では九九八十一,八九七十二と始める形で排列して覚えられていたことによるのである(この順による排列は唐代まで続いた)。したがって中国の古文書では九九,または九九之術という言葉が使われているのであり,日本はそれにならったのである。
古来有名な算術の問題の例をあげよう。そのうちとくに次の〈つるかめ算〉の歴史はたいへん古い。中国の《孫子算経》(六朝時代の書といわれている)にはキジとウサギで出されている。日本では,今村知商の《因帰算歌》(1640)にやはりキジとウサギで出ているのが,いちばん古いようである。ツルとカメになったのは,坂部広胖の《算法点竄指南録》(1810)が最初のようである。
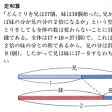
つるかめ算
ツルとカメ合わせて12匹いる。その足の数は全部で32本であるという。ツル,カメそれぞれ何匹か。
解 まず足を2本ずつ数えると24本,残り32-24=8本はカメの足が1匹につき2本ずつまだ残っていることによる。したがってカメは4匹,ツルは12-4=8匹。
過不足算
ミカンを分けるのに,1人に3個ずつとすると4個余り,4個ずつにすると2個不足するという。ミカンの数および人数を求めよ。
解 1人分を1個増したとき,必要数が4+2=6個増したのだから,人数は6人,ミカンの数は3×6+4=22個。
旅人算
(1)甲が毎時3kmの速さで歩く。甲の出発後2時間のとき乙が同じ地点を出発して毎時5kmの速さで追いかけるとすれば,乙が甲に追いつくのは,乙の出発後何時間後か。
(2)24km離れた2地点A,Bがある。甲はAから毎時3km,乙はBから毎時5kmの速さで向かい合って歩く。出発が同時であれば,2人が出会うのは出発後何時間後か。
(1)の型を追いかけ算,(2)の型を出会い算ということもある。
解(1) 乙が出発するとき,甲は3×2km先にいる。乙の出発後,2人は毎時2kmずつ近づく。したがって,追いつくのは3時間後。
解(2) 2人は毎時3+5kmずつ近づく。したがって,24÷8=3時間後に2人は出会う。
和差算
甲乙二つの数があり,その和は25,その差は11である。甲,乙2数を求めよ。
解 和と差の和25+11=36は甲,乙のうち,大きいほうの2倍である。したがって,大きいほうは18,小さいほうは25-18=7。
流水算
ある川を舟でいくのに,下れば毎時6km,上れば毎時4kmの速さであるという。舟の静水での速さと川の流れの速さとを求めよ。この問題では,川の流れの速さが一定であり,舟の水に対する速さが一定であるという前提が必要であるが,通常それは断らずに前提として認めている。
解 舟の速さと流れの速さについて,和差算が適用されるから,舟の速さは(6+4)÷2=5km/h,流れの速さは6-5=1km/h。
年齢算
甲の年齢は35歳,乙の年齢は10歳であるという。何年後に甲の年齢は乙の年齢の2倍になっているか。この基本は,何年後の時点を考えても,甲乙の年齢の差が一定ということにある。したがって,この型の問題を定差算ということもある。
解 2人の年齢の差は25,したがって,乙の年齢が25のとき,甲の年齢は乙の年齢の2倍になる。ゆえに,25-10=15年後。
植木算
(1)周囲500mの池の堤に10m間隔で木を植える。何本植えることになるか。(2)道路の片側に10m間隔で木を植える。木の植わる区間が500mであれば,何本植えることになるか。(3)2本の鉄塔があり,その間隔は500mである。この2本の鉄塔を結ぶ線上に,10m間隔で木を植えるとしたら,何本植えることになるか。
解(1) 500÷10=50本。
解(2) 両端にも植えるのだから,(1)より1本多くなり,51本。
解(3) 両端には植えられないから,(1)より1本少なくなり49本。
仕事算
ある仕事を仕上げるのに,甲,乙いずれも1人では20日,丙1人では15日かかるという。3人が協力すれば何日で仕上げることができるか。この問題では,協力によって得られる仕事の分量が,別々に仕事をしたときの量の和にちょうどなっているという前提が暗黙のうちに仮定されている。
解 全仕事量に対する割合で考える。甲,乙は1日に1/20,丙は1/15をする。1/20+1/20+1/15=1/6であるから,3人が協力すれば,1日に全量の1/6ができる。したがって,6日で仕上がる。
次に和算などがとり上げた問題で,上記の意味の算術と考えられるものを補う。
ねずみ算
《塵劫記》(1627)は次の内容を扱っている。1組のねずみの夫婦から出発して,毎月1回雌雄6匹ずつのねずみを生み,子ねずみも同様にねずみを生むとすれば,12ヵ月後には何匹になるか。答えは,毎月7倍になるから,2×712。実際にこのようになるわけではないが,増大が速い例としてとらえられ,“ねずみ算式に増える”という言い回しが現代にも残っている。7倍の代りに2倍でも非常に速く増大する。それを利用した話はいろいろある。曾呂利新左衛門が太閤秀吉に将棋盤の目の一つに米粒一つをおき,次の目に二つ,その次の目に四つと,以下,順次2倍ずつ置いた分だけほしいといったという話があるが,総計(281-1)粒となり,約4×1017石になる。これもねずみ算式増大の例といえる。
百五減算
ある数を,3,5,7で割ったときの余りを指示して,もとの数を求める問題である。105は3,5,7の最小公倍数ゆえ,一つの答えがαであれば,α+105n(n=0,±1,±2,……)が答えの全部である。そこで,和算では自然数の答えのうち最小のものを求めた。3,5,7で割った余りが,それぞれa,b,cであれば,70a+21b+15cが一つの答えになる(それは,70,21,15をそれぞれ3,5,7で割ると1余るから)ので,70a+21b+15cから105の倍数を引いて答えを求めた。これが百五減算という言葉の由来である。
この問題をもっと一般化して考えるならば,次のようにまとめられる。a1,a2,……,anが互いに素(共通因数がない意)の自然数であるとき,n個の整数b1,b2,……,bnを与えれば,i=1,2,……,nについてx-biがaiの倍数であるようなxがあり,その一つは次のようにして求められる。a2a3……anの倍数でa1で割って1余る数c1を見つける。以下,同様にa1a2……an÷aiの倍数で,aiで割って1余る数ciをとる。するとc1b1+c2b2+……+cnbnは一つの解である。他の解はこれとの差がa1a2……anの倍数であるような数である。
執筆者:永田 雅宜
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「算術」の意味・わかりやすい解説
算術
さんじゅつ
算術は、古く中国では、数学全般を意味する語として用いられ、それがそのまま日本にも伝わっていたが、日本では、明治の初め西洋の数学を受け入れる際に、英語のarithmeticに対する訳語として、この語を採用した。この際に、数の理論を研究する数学の分野としての名称と、学校で数を中心とする教育を行う教科としての名称とが、未分化のまま用いられ、そのままあとまで引き継がれていった。しかし今日では、数学の分野としては、整数論ないし数論というほうが一般的であり、教科名としては、1941年(昭和16)の小学校から国民学校への制度改革以来、算数とよぶようになった。
今日算術という語を用いる場合には、明治から昭和にかけての学校教育のなかでの算術のイメージをもとにしている場合が多い。この時期の算術科の内容は、命数法、記数法、整数、小数、分数の四則、諸等数(各種の量の単位と、複数の単位を伴った数値の扱い)、比と比例、日常諸算などからなり、範例と練習とを通じて計算法に習熟すること、日常生活に四則を応用すること、考え方を練ることをそのねらいとしていた。考え方を練るため、実生活上の意味はなくとも、謎(なぞ)としてはおもしろ味のある「四則応用問題」(文章題)が課せられた。これらは、代数を学んでしまえば統一的な方法でやさしく解けるものであるが、算術のなかでは、文字を用いず問題場面に即して、適切な観点変更を行って解くことを求めたもので、その手法に応じ、何々算といった名称でよばれていた。
[島田 茂]

算術の四則応用問題(1)

算術の四則応用問題(2)
算術の四則応用問題(3)

算術の四則応用問題(4)

算術の四則応用問題(5)

算術の四則応用問題(6)

算術の四則応用問題(7)

算術の四則応用問題(8)

算術の四則応用問題(9)

算術の四則応用問題(10)
普及版 字通 「算術」の読み・字形・画数・意味
【算術】さんじゆつ
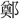 玄伝〕
玄伝〕 爲(た)るを樂しまず。~
爲(た)るを樂しまず。~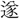 に太學に
に太學に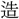 (いた)りて業を受く。京兆の第五元先に師事し、始めて京氏易・
(いた)りて業を受く。京兆の第五元先に師事し、始めて京氏易・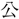 羊春秋・三統
羊春秋・三統 ・九
・九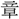 算
算 に
に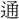 ず。
ず。字通「算」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
百科事典マイペディア 「算術」の意味・わかりやすい解説
算術【さんじゅつ】
→関連項目算数|数学
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の算術の言及
【自由七科】より
…自由学芸とも訳され,思想的源流としては,古代ギリシアの,肉体労働から解放された自由人にふさわしい教養という考え方にさかのぼり,実利性や職業性や専門性を志向する学問と対立する。ローマ末期の4~5世紀に七つの科目に限定され,言語に関する三科trivium,すなわち文法grammatica,修辞学rhetorica,論理学logica(弁証法dialecticaと呼ばれることもある)と数に関連した四科quadrivium,すなわち算術arithmetica,幾何geometrica,音楽musica(もしくはharmonia),天文学astronomiaに区分される。これらは本来異教徒の学問であるが,それがキリスト教世界の法学や医学のための基礎科目だけでなく神学の基礎科目となったことは,ヘレニズムとヘブライズムとの融合の具体的あらわれである。…
※「算術」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
1 食肉目クマ科の哺乳類の総称。全般に大形で、がっしりした体格をし、足の裏をかかとまで地面につけて歩く。ヨーロッパ・アジア・北アメリカおよび南アメリカ北部に分布し、ホッキョクグマ・マレーグマなど7種が...

