翻訳|crystal
共同通信ニュース用語解説 「結晶」の解説
結晶
更新日:
出典 共同通信社 共同通信ニュース用語解説共同通信ニュース用語解説について 情報
精選版 日本国語大辞典 「結晶」の意味・読み・例文・類語
けっ‐しょう‥シャウ【結晶】
- 〘 名詞 〙
- ① 規則正しい数個の平面で囲まれる鉱物など。科学的には原子、イオン、分子などが、対称的、周期的に規則正しく配列し、外形も対称の関係にあるいくつかの限られた平面によってできた多面体をなしている固体をいう。金属などのように、境界がいりくんで、平面で囲まれていないものでも、X線の回折現象を示すものは含めていう。〔舎密開宗(1837‐47)〕
- ② 愛、努力、悲しみなど、抽象的なある事柄が積み重なり、集まった結果、他のある形をとって現われること。また、その結果として現われたもの。必ずしも有形物をさすとは限らない。所産。成果。
- [初出の実例]「独り見て独り悦び毀誉を外にして優然たるは(或少数を除き)是自負の骨頂にて見得の結晶(ケッシャウ)せる姿なるべし」(出典:春迺屋漫筆(1891)〈坪内逍遙〉壱円紙幣の履歴ばなし)
改訂新版 世界大百科事典 「結晶」の意味・わかりやすい解説
結晶 (けっしょう)
crystal
水晶の結晶が図1に見られるように六角柱の形をとることはよく知られている。しかし,結晶には必ずしも,このような規則正しい外形をとらないものも多く,結晶の本質は次に述べるようなそれが示す性質に関連している。
自由に選んだ一つの方向においての物質のある性質の測定値が,その物質中のすべての点で互いに等しいとき,その物質は均質であるという。その性質の測定値をベクトルで表せば,物質が均質であることは図2のように示される。物質の内部の任意の点Oにおいて,ある性質の測定値(例えば電気伝導度の値)が,図3のaやbのように方向によって異なるとき,その物質はその性質について異方的であるといい,cのようにそれが方向に無関係に一定しているとき,等方的であるという。
ともに異方的であっても,図3のaとbとは互いに異なる。点Oにおける測定値のベクトルの先端の図形は,aではOの周りに180度回転しないと最初に与えられている図形とは一致しないが,bでは90度回転ごとに最初のものに重なる。このように,ある図形(あるいは物体)Xを動かして最初の形に重ね合わせることをXの対称操作といい,Xのもつすべての対称操作の集りをXの対称symmetryという。対称操作を具体的に表すものを対称要素という。図3のaは360度回転の間に2回最初の形に重なり,bは4回重なるので,aの対称操作は2回回転,bのそれは4回回転,またO点で紙面に垂直な軸を考えて,aの対称要素を2回回転軸,bのそれを4回回転軸という。以上に対して,図3のcの等方的な場合には,測定値の図形はO軸の周りに任意の角度回せばそれ自身に重なるところの円だけである。すなわち,対称の種類が問題となるのは,図形や物体が異方的である場合に限られる。
均質な固体物質が図4のaのようにある性質について異方的であるとき,その物質は結晶質crystallineであるといい,あらゆる性質が図4のbのように等方的であるとき,その物質は無定形質あるいは非晶質(アモルファスamorphous)であるという。結晶質の物質の中には,ある性質については異方的であるが,他の性質については等方的であるようなものもある。例えば食塩NaClの結晶は,熱膨張率については異方的であるが,その中を通る光の速度については等方的である。
物体全体が一様に結晶質である場合,これを単結晶と呼ぶ。また,それが小さな単結晶が多く集まって,互いに不規則に向きを異にしてくっつきあっているものを多結晶と呼ぶ。単結晶の例には図1のような天然に産する六角柱状の水晶SiO2の結晶がある。またダイヤモンドをはじめ,透明な宝石はいずれも単結晶から切り出して磨いたものである。多結晶の例には,器具類や機械類の材質である種々の金属がある。なお,2個の単結晶が向きを異にしてくっつきあっていて,その接合に一定の規則性がある場合があり,それを双晶と呼ぶ。図5は向きあった二つの柱面が大きくなることによって扁平となった水晶の2個の単結晶の双晶である。また無定形物質の例としてはゴムやガラスがある。さらに,多結晶中で単結晶が連続的な向きの変化をもって分布しているものがあり,その代表的なものには木材などの繊維質のものがある。以後,本項目において結晶という場合はすべて単結晶のこととする。
結晶の形態
紀元前のギリシアでは,水晶は氷が異常な低温に冷やされたために,常温でも水にもどらなくなったものと考えられた。そのために,水晶は氷(ギリシア語でkrystallos)と同じとみられ,これがcrystal(水晶,結晶)の語源である。
面角一定の法則
前述の水晶の結晶が六角柱の形をとるように,結晶は,平面で囲まれた形をとることができるのがその特徴であって,これらの平面のおのおのを結晶面という。同じ種類の結晶面でも,結晶ができたときの環境次第で,互いに異なった大きさになることがある。しかし,対応する面の間の角度は一定している。図6のように水晶の柱に垂直な切断面が互いに異なった形になっていても,隣りあった面の間の角度は,この場合には120度と一定していることが経験的にわかっている。これを面角一定の法則,あるいは面角不変の法則という。このように,結晶形態において一定に保たれるものは,面の相互の位置ではなくて,それら相互の傾きであり,それゆえ任意の1点Oから各面に下ろした垂線の束がその結晶について一定しているのである。すなわち,結晶形態の考察においては,結晶面を自由に平行移動させて考えてもさしつかえない。
有理指数の法則
結晶形態に現れる稜(結晶面の交線)の中で,同一平面上にない任意の3稜を選んで,これらをこの結晶の結晶軸a,b,cと名づけ,結晶形態を記述する座標軸とすることができる。これらの座標軸は一般には一つの斜交座標系を構成する。次に結晶軸のいずれとも交わる面の中の任意の一つをとって,これを基準面とする。結晶軸と基準面P0との関係を図7のaに示す。次いでbのように,1点Oからaの3軸にそれぞれ平行に軸a,b,cをとり,基準面に平行な面P0をおくと,前に述べたように結晶面は平行移動して考えてもさしつかえないから,bはaと同等なものである。P0と3軸との交点をそれぞれA0,B0,C0とする。aで3軸と基準面とを定めたことは,bで3軸の方向とOA0:OB0:OC0の比の値を決めたことに相当する。この比を結晶軸a,b,cのそれぞれの方向の長さの単位の比と考え,それを軸率と呼ぶ。またbのように軸間の角をα,β,γと名づけて,それらを軸角という。このように決めることは,一般には斜交軸をとり,さらに各軸方向の長さの単位が互いに異なるという複雑な座標系をとることになる。しかし,この座標系を用いれば,結晶には次に述べる法則が成立し,結晶の記述が結局はたいへん簡単になる。
基準面P0以外の面Pが3軸を切る長さをOA,OB,OCとし,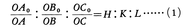
とおく。結晶に成立する簡単な法則というのは,H,K,Lのおのおのは簡単な有理数,すなわち分数の形にしたときにその分子・分母ともにあまり大きな整数とはならないような有理数となるというもので,これを有理指数の法則という。
面指数
H,K,Lの分母の最小公倍数をM,分子の最大公約数をDとし,MH/D=h,MK/D=k,ML/D=lとすれば,h,k,lは1以外の公約数をもたない整数のうち値の小さなものであり,H:K:L=h:k:lであるから,(1)は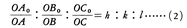
となる。これらのh,k,lを面Pの指数といい,面Pを(hkl)によって表して,これを面記号という。基準面の面記号は(111)である。図8のaは面がa,b,cの3軸の単位の長さをそれぞれ1/2,1/2,1/3で切る(223)である場合を示し,bはb軸を正の方向で切る右側の(212)と,負の方向で切る左側の場合が示されており,後者は指数kの上にマイナス符号をつけて,(212)と表す。cは(210)である。
晶帯
a,b,c方向にそれぞれx,y,z軸をとって,原点を通る(hkl)の方程式を書けば,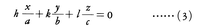
となる。(h1k1l1)と(h2k2l2)との交線は,(3)の形の二つの方程式の解として,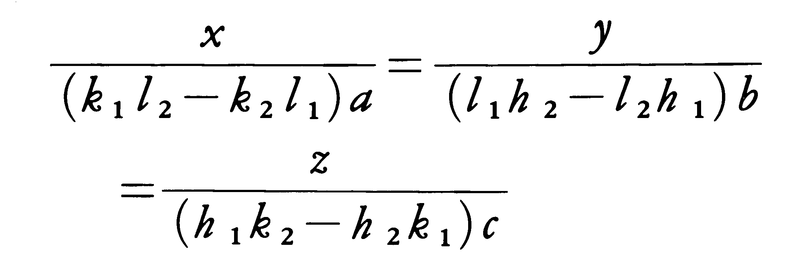
で与えられる。二つ以上の面に共通する方向を晶帯といい,
U:V:W=(k1l2-k2l1):(l1h2-l2h1):(h1k2-h2k1)
によって,互いに素な整数の中で値の小さなものU,V,Wを選ぶことができる。これを(h1k1l1)と(h2k2l2)が与える晶帯の指数といい,その晶帯を[UVW]という記号で表す。
が晶帯[UVW]を与える方程式で,a,b,c3軸方向の座標の成分がそれぞれUa,Vb,Wcである点に向かって原点から引いた直線が[UVW]の方向を表す。それゆえa軸は[100],b軸は[010],c軸は[001]とも表すことができる。
結晶の構造
結晶が均質で異方的であり,面角一定の法則と有理指数の法則に従うことは,結晶についての直接の観察,すなわち結晶の巨視的状態の測定によって確かめることができる。一方,結晶の内部においては,結晶ごとにある定まった配列をした原子の集りがその結晶の構成単位となって,それらの単位が空間的に一定の繰返しを保って互いに平行に配置している。このことは,結晶によるX線,電子線,あるいは中性子線の回折現象を利用して知ることができる。これは結晶の微視的状態と呼ばれるものである。例えば図9のaは大円で表した原子と,その向かって左下側にある小円の原子との1組で構成単位を形成して,この単位が前後・左右・上下にそれぞれの方向ごとに定まったある間隔で繰り返して互いに平行に並んでいる結晶構造を示す。
結晶格子
これらの単位は図9のaに便宜的に描いた破線の枠に従って配列しているとみることができるので,bのようにこの枠(これを空間格子,結晶格子あるいは単に格子という)を取り出して,それが限りない広がりをもつと理想化して考えることにする。bの前後・左右・上下の3線の交点を格子点という。aでは格子点に大円の原子が一致しているように描いてあるが,もともと結晶格子は構成単位の繰返しの方向と間隔のみを表すものであって,格子の原点に当たる格子点を結晶構造のどこにとるかはまったく自由である。任意の二つの格子点を結ぶ線を格子線という。その線上には格子点が等間隔に並んでいて,それは一次元格子となっている。その上の隣どうしの点の間隔を周期という。1格子点で交わる2本の格子線が乗る面を格子面といい,格子面の上には格子点が二次元的な平面格子をつくっている。結晶格子の中では,一つの格子面に対して,それと合同でそれに平行な格子面が限りなく多く存在する。これら同種で隣りあう格子面の間の垂直距離を面間距離という。任意の格子点を通る同一平面上にない3格子線をとり,それらの周期を3稜とする平行六面体を単位胞あるいは単位格子という。図9のcに見られるように,一つの空間格子において無限に多くの単位胞のとり方がある。単位胞の8隅のみに格子点があるとき,それを単純単位胞といい(cの左側の2種),単位胞の面上あるいは内部にも格子点を含むものを多重単位胞という(cの右側のもの)。このように,結晶を微視的に見ると,周期が通常10⁻6~10⁻8cm程度の格子構造を形成している。
結晶の微視的対称
並進対称
結晶格子は結晶の構成単位がそれに従って一定間隔で互いに平行に配列する枠であるから,結晶構造を限りなく広がったものと理想化して考えれば--肉眼で見える大きさの結晶の中には莫大な数の構成単位が含まれているから,結晶の内部構造を考える限りは,構成単位の繰返しは無限であるとしても大きな誤差を与えない--,結晶格子の任意の2格子点間のベクトルに相当するだけ結晶構造全体を平行移動しても,その結果は移動前のものとまったく区別がつかない。このことは結晶構造が三次元の並進対称(平行移動を対称操作とする対称)をもっていることであり,この並進対称を具体的に表す結晶格子は結晶構造の対称要素の一種である。最初に与えられた図形あるいは物体Xの部分Aに,Xに対称操作を施した結果においてXの部分Bが重なったときに,AとBとは互いに対称的に同価であるという。すべての格子点は互いに並進対称的に同価である。
回転対称
結晶によっては,格子並進対称以外の対称をも示すものがある。例えばある軸の周りに結晶構造を360°/nだけ回転させると,回転前のものと重なるというn回回転対称をもつことがある。この場合に,結晶構造は空間格子に従った構造であり,空間格子とは同じものがその格子の周期に従って繰り返して互いに平行に並んでいることを意味するから,同じn回回転軸が格子の周期に従って互いに平行に並んでいなければならない。これらのn回回転軸の中で軸間の垂直距離の最も短い2本をN1とN2とする。図10はこれらの軸の方向から見たもので,N1はn回回転軸であるから,その周りにN2から360°/nだけ隔たったところにはN2と同価なn回回転軸N3がなければならない。図10のaにおいて,もしn>6であれば,N2N3<N1N2となって,N1N2が軸間の最短垂直距離であるという最初に決めたことに矛盾する。それゆえn≦6でなければならない。またn=5のときには,図10のbによってN3N4<N1N2となることがわかり,これも不都合である。残るn=1,2,3,4および6の場合にはこのような不都合は生じない。それゆえ結晶には1回,2回,3回,4回および6回回転軸だけしか存在しない。この事実を回転対称の結晶学的制限という。これら5種の回転軸を図11に示す。球上に亜鈴が配列した図形はそれぞれの回転対称をもった図形の例である。回転対称は1,2,3,4および6と単なる数字で表すことになっている。
回反対称
上記の回転のほかに,並進対称でない対称として結晶がもちうるものには回反対称がある。これは図12のようにある軸(これを回反軸と呼ぶ)の周りのn回回転操作に引き続いてその回転軸上に定められた1点Oでの反転--その点を座標の原点とするとき,(x,y,z)の点を(-x,-y,-z)に移す操作--を与える合成操作をn回回反操作といい,回転と反転の順序を入れ換えても結果は同じである。結晶構造がn回回反対称をもつとき,その結晶格子はn回回転対称をもたねばならないことが容易に証明されるから,回反の場合のnも結晶学的制限に従い,それらを1,2,3,4,6で表す。図13で示す1は反転そのものであり,この対称要素は対称心と呼ばれる。
鏡映対称
また図形が2をもつと,それは反転の点を通って回反軸に垂直な面の側の図形の部分が,他の側の部分をその面で映したような関係になっているので,その対称要素は鏡映面と呼ばれ,この場合は2の代りに鏡mirrorのmで表す。
らせん対称
さらに,回転と回転軸の方向の並進tとの合成であるらせん(螺旋)も結晶構造の対称操作となりうる。この名はこれを繰り返すと点が軸を取り巻くらせんの上に並ぶことによる(図14)。結晶構造がn回らせん対称をもつとき,その結晶格子はn回回転対称をもつことが証明できるから,らせんも結晶学的制限に従う。またn回らせん操作をn度繰り返すと,回転の結果は最初にもどるから,らせん軸方向の単なる並進ntとなり,それによって結晶構造がそれ自身に重ねられるのであるから,ntは結晶格子の並進の一つに一致しなければならない。その方向の周期を表すベクトルをl(|l|>|t|),mをnより小さい自然数とすれば,上のことはml=ntが成立することを意味し,らせんをnmの形に表すことができるわけである。したがって,らせんには21,31,32,41,42,43,61,62,63,64,65の11種類があり,図15で示すように,これらの中で31と32,41と43,61と65および62と64とはそれぞれの対の中の二つが右回りと左回りの関係にあり,また42と62と64は2を兼ね,63は3を兼ねている。
映進対称
回転と並進との合成でらせんが生じたが,回反と並進との合成では,n=2以外の場合には,同じ回反軸が異なった位置に移されたものとなるだけである。n=2のときには,鏡映とその面に平行な並進tとの合成である映進と呼ばれる新しい対称操作が生ずる(図16)。映進を2回繰り返すとtの方向の格子並進となる。それが結晶のa方向の単位を表すベクトルaとなる場合には,この映進をaで表し,そのときはt=a/2である。同様にbやcで表される映進がある。tが1/2(a±b),1/2(b±c),1/2(c±a)のいずれかに等しいとき,この映進をnで表す。後に述べるように格子が底心,面心あるいは体心の場合には,tが1/4(a±b)などの一つ,あるいは1/4(a±b±c)に等しくなる映進が可能で,これらはdという記号で表される。
空間群
空間格子と上記の回転,回反(反転と鏡映とを含む),らせん,映進などの対称要素とが空間的にある配列をしていて,それらの対称要素のいずれもが一つの結晶構造をそれ自身に重ね合わせるとき,これらの対称要素の配列を空間群という。すなわち空間群とは一つの結晶構造をそれ自身に重ね合わせるあらゆる対称操作の集合である。その最も簡単な例として,図17のaには格子並進Tのみのもの,bにはTと紙面に垂直な2回回転軸2(黒いレンズで示した)との組合せ,cにはTと紙面に垂直な鏡映m(実線で示した)との組合せの空間群を示す。それぞれの図に配列した小円は,これらの対称によって互いに同価となる点である。また矢印は並進の二つの周期を示し,第3の周期は紙面(投影面)に垂直とする。いずれの図も無限に広がる図形の一部を示す。
空間“群”というのは次の理由による。与えられた結晶構造Xをそれ自身に重ね合わすすべての対称操作の集合Gsにおいて,その中の任意の対称操作g1によってXの部分AがXの他の部分Bに重ね合わされながらXは全体としてXに重ね合わされ,それに引き続いて対称操作g2を施すことによってXの部分BがXの部分Cに重ね合わされながらXは全体としてXに重ね合わされる。すなわちg1に引き続いてg2をおこなった結果は,部分Aを部分Cに重ね合わせながらXをXに重ね合わせることになるから,これもまたXの対称操作の一つであって,それは例えばg3と名づけられて既にGsの中にあるはずである。g1に引き続いてg2を施すことをこれら2操作間の演算( で表す)と定義すれば,上の事情はg1
で表す)と定義すれば,上の事情はg1 g2=g3となることであり,この演算に関してGsは代数学で定義される群を構成していることを示すことができる。そのためGsを空間群という。
g2=g3となることであり,この演算に関してGsは代数学で定義される群を構成していることを示すことができる。そのためGsを空間群という。
三次元のあらゆる種類の結晶構造をそれ自身に重ね合わせる対称操作の集合,つまり空間群には,互いに異なった230種類のものがあることを,理論的にそれらを次々に導き出して最後に数えあげることによって証明することができる。
結晶の巨視的対称
上述の結晶の微視的対称との関連において,結晶の巨視的対称を考える。結晶の巨視的観察における〈点〉とは,微視的にはその中にきわめて多くの格子点を含むある半径をもった球とみることができる。この球の互いに異なった位置にあるものどうしを比較すると,図18のように,格子点の配列はそれら二つの球の内部では互いに等しく,球面に近いところでは球面に相対的に互いに異なる。しかし,これらの球面付近の格子点の数は,球の内部の格子点の数に比してきわめてわずかであるから,格子点の配列という観点においては球相互の差はないとみてさしつかえない。このことは結晶が巨視的には均質となることを示している。
また,結晶の諸性質は外部からの作用に対する結晶の構成単位の反作用の合成であり,この合成反作用は構成単位の配列の仕方を反映するが,構成単位の配列は結晶格子に従っているからそれは異方的であり,それゆえ結晶には巨視的に異方性が観察されることになる。ただし,結晶の性質の対称は結晶構造の対称Gsには含まれないある対称操作をGsにつけ加えたものとなることが多いので,結晶の巨視的対称の幾何学的考察には,Gsに余分なものをつけ加えることのないことが経験的に知られているところの結晶形態の対称に注目しなければならない。
結晶形態に現れる結晶面のおのおのはその結晶の構造のある格子面であることが経験的に知られている。逆にいえば,すべての格子面は結晶面となりうる可能性を多かれ少なかれもっている。また結晶面の交線である稜は格子面の交線である格子線であり,同一平面上にないある3稜を結晶軸としたのであるから,結晶軸のおのおのはある格子線である。このことは,結晶軸は必ずしも結晶形態に現れた稜には限らず,形態の記述に便利な格子線の方向にとりかえてもよいことを意味している。また,結晶面として現れるある格子面と対称的に同価な他の格子面もやはり結晶面として形態に現れることも経験的に知られている。
点群,結晶族
微視的なn回らせんや映進の並進成分tは巨視的には見ることができないから,それらは巨視的にはそれぞれn回回転と鏡映とに等しくなり,また微視的な格子並進も巨視的には均質な連続体となるから,その結晶の任意の点Oを原点にとって,すべての対称要素がOを通るとみなしてよいことになる。互いに平行に繰り返して存在する結晶構造の微視的な対称要素と,それらと方向を同じくして原点Oを通る巨視的な対称要素との対応を矢印で示せば,n回回転およびらせん軸→n回回転軸,n回回反軸(n>2)→n回回反軸,鏡映面および映進面→鏡映面,対称心→対称心となる。これらの対応によって得られる巨視的な対称操作の集合も数学上の群をなすことが証明され,しかもこれらの対称要素はいずれも原点Oを通るから,この群は点群とよばれる。結晶を微視的に見た場合,空間群は230種類可能であったが,巨視的に見るとその対称は32種の点群に限られ,これらを結晶族または晶族という。
結晶系
空間格子の格子点の一つを固定しての運動によって,格子をそれ自身に重ね合わすような対称操作をすべて含む点群を求めると,表における第4列の7種のものが得られ,これらを完面像点群(晶族)という。これらの点群によってそれ自身に重ねられる結晶格子は,その格子線の方向や周期が対称を反映しており,今後は結晶軸も対称を表す格子線の方向にとりかえることにする。そのようにしたときに得られる3軸の周期と軸角にみられる関係を第2列に示す。完面像点群によって分類される7種の結晶軸のとり方による結晶の分類を結晶系もしくは晶系といい,これら7晶系の名称を第1列に与える。これらの中で三方晶系のみには,完面像点群3mによってそれ自身に重ねられる格子には軸のとり方が異なる2種類のものがある。
ブラベ格子
表の第2列の指定に従って結晶軸をとったときに,結晶系によっては単純単位胞以外に多重単位胞をもとれる場合があり,これらを数えあげると第3列と図19に示した合計14の型の格子が得られる。この14の型の格子を,これを研究したA.ブラベの名を冠してブラベ格子と呼ぶ。図19はブラベ格子のおのおのの単位胞を示し,後ろ下方の格子点を原点として,前,右,上の方向((10))のみは,下方の格子点を原点として,前,右,左の方向がそれぞれa,b,c軸である。第3列のPは単純格子,Cは底心格子,Iは体心格子,Fは面心格子,Rは菱面体格子を表す記号で,それぞれに付けた(10)などは記号ではなく,図19に対比させる番号である。単純格子は単位胞の角にだけ格子点がある。底心格子は単位胞の角と底面の中心に格子点がある。体心格子は単位胞の角と中央に格子点がある。面心格子は単位胞の角と各面の中心に格子点がある。
完面像点群のおのおののある部分に相当する点群(完面像点群の部分群)には,第3列のブラベ格子をそれ自身に重ね合わせるものがあり,それらすべてを第5列に示す。例えば完面像点群mmmの部分群は,それ自身も自己の部分とみなして形式的に部分群に含めれば,mmm,mm2,222,2/m,m,2,1,1の8種であるが,この中でmmmと同じく(4)(5)(6)および(7)のブラベ格子をそれ自身に重ね合わせるものはmmm,mm2,222の3種のみである。斜方晶系とはこれら3種の点群の集りであるということもできる。
点群記号
各結晶系における点群の記号が対応する方向とそれらを書き表す順序を表の第6列に示す。そこでaとか[110]とかいうときには,その方向にある回転軸あるいは回反軸の種類,またはその方向に垂直な鏡映面mがあることが示され,ある方向に2,4あるいは6の回転軸があるとともにそれに垂直なmがある場合には,それぞれ2/m,4/mあるいは6/mで表す。三斜晶系以外では,1は略して書かない。第6列の(1)(2)などは図20の同じものに対応する。
点群と結晶形態
点群の例として図21のaにm3m,bに432,cに23を示す。これらの図の中の四角形,三角形,レンズ形はそれぞれ4回,3回,2回回転軸を,またaの面はいずれも鏡映面mである。この中で完面像点群m3mでは,aに垂直なmと[111]方向の3と[110]方向に垂直なmとがあれば,aに示されている4と2などの他の対称要素は必然的に現れてくることになる。これらの3点群のそれぞれにおいて,面(321)が現れたとすると,それと対称的に同価な面も結晶形態に現れ,図22に示すように,m3mではaの48面体となり,これは完面像と呼ばれる。432はbの24面から成り,完面像の半分の面数をもつため半面像と呼ばれる。23はcの12面からなり,完面像の1/4の面数をもつため四半面像と呼ばれる。
→結晶学 →結晶光学 →結晶構造 →結晶成長 →鉱物 →固体
執筆者:定永 両一
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「結晶」の意味・わかりやすい解説
結晶
けっしょう
crystal
物質の固体における存在状態の一つ。外見上は、平滑な多角形の面が鋭い稜(りょう)によって組み合わされた多面体となる。微視的には、その物質を構成する原子、分子、イオンなどが三次元的に周期性のある配列をとることが特徴である。三次元的配列の規則性は空間格子(結晶格子)とその対称性によって幾何学的に表現され、その規則性のために光学的性質、機械的性質、電気的性質、磁気的性質などの物理的性質が結晶内の方向によって異なる、つまり異方性を示すことも結晶の特徴である。ガラスのような物質にはこのような結晶としての特徴はなく、非晶質とよばれて結晶とは区別される。
肉眼では結晶としての外見上の特徴が観察されない粉末であっても、顕微鏡ではそれが観察されることもある。1個の結晶が結晶格子と同じ軸方向の性質を示すものを単結晶single crystalという。実際の結晶では、さまざまな配向の単結晶が凝集して1個の結晶になっているものがあり、これを多結晶polycrystalという。単結晶であっても、このような構造の乱れは小規模に存在していると考えられている。高分子やガラスのような非晶質でも、部分的には結晶構造をもつことが多く、固体の存在状態としては結晶になるほうが安定であると考えられている。古いガラスでは部分的に結晶化が進行してその部分が失透し、ガラス特有の粘性が失われて、もろくなることがある。
液体であっても、その構成分子の形が棒状や板状であると、それらの分子が規則的に配向して、結晶のような諸性質の異方性を示すことがあり、そのような液体を液晶という。
[岩本振武 2015年8月19日]
球体の充填
高温度では液体や気体になっている物質が温度の低下によって結晶化するのは、その物質の構成粒子の運動エネルギーが温度の低下によって小さくなり、粒子間の引力の効果のほうが大きくなるからである。したがって、結晶化の際には、原子、分子、イオンなどの構成粒子は、なるべく空隙(くうげき)を小さくするように凝集する。
これらの粒子のもっとも簡単なものは原子であり、貴ガス(希ガス)や金属元素の単体の結晶は同寸法の剛体球が凝集したものと考えることができる。平面上に剛体球をなるべく空隙が小さくなるように並べると、1個の球がそれぞれ6個の球に囲まれる配列となる。
[岩本振武 2015年8月19日]
最密構造
この球の層を順次積み上げると三次元の最密構造が得られる。いま第1層の球の中心をaとし、その配列をA層とする。A層には、3個の球の間の空隙としてbおよびcの2種類が生ずる。そのどちらも同価であるから、第2層は球の中心がbの空隙の上にくるように積み上げたとする。すると、次の層を積み上げるやり方は二通りある。一つは第1層と同じ配列Aをのせるやり方であり、もう一つは第1層の空隙cの上に第3層をのせるやり方である。前者のABの繰り返しで積み上げた構造を六方最密構造といい、配列Aの各球の中心を格子点とすると単純六方格子ができる。ABCを繰り返す後者で生ずるのは立方最密構造であり、各球の中心を格子点とすると面心立方格子を得る。いずれの場合も、単位格子(単位胞)の中で球が占める体積(充填(じゅうてん)率)は単位格子の体積の74%である。最密構造よりやや空隙の体積が大きくなる体心立方構造も単体の結晶にはよくみられるが、この構造での充填率は68%になる。
立方最密構造、六方最密構造のいずれにおいても、1個の球には12個の球が隣接する。体心立方構造ではその個数は8となるが、隣接する6個の単位格子の体心にあるやや離れた球まで含めれば14となる。このように、結晶中のある原子に着目し、その原子に隣接して位置する原子の個数を、その原子の配位数という。
最密構造で詰め込まれた球の間には2種類の空隙を生ずる。一つは4個の球に囲まれた空隙で、その中心は各球の中心を結んで得られる正四面体の中心になっている。別の空隙は6個の球に囲まれ、その中心は各球の中心を結んで得られる正八面体の中心になっている。体心立方構造においても、それぞれ4個および6個の球に囲まれた空隙があるが、正四面体および正八面体よりかなりひずんだ構造となる。これらの空隙にほかの原子やイオンが入り込むと化合物の結晶になるが、化合物では原子、分子、イオンの形や寸法の組合せがさまざまに変わるから、それに応じて結晶の構造も複雑になる。
[岩本振武 2015年8月19日]
空間格子
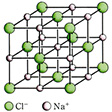
ある物質が一定の結晶構造をもつならば、その単結晶には構造を反映した特徴が現れる。同一物質の結晶が、成長した媒質の条件によって異なる外形を示すこともある。たとえば、純水溶液から成長した塩化ナトリウムの結晶は立方体となるが、10%尿素水溶液から成長したものは正八面体となることが多い。このような外形の特徴を晶癖(しょうへき)というが、いずれも結晶内の原子の配列状態を反映したものである。塩化ナトリウムでは、面心立方格子の構造をもっており、立方体の外形を示すことは容易に理解できよう。またこの立方体の面心の位置を結ぶと正八面体になることも簡単な作図から理解できる。
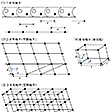
結晶構造の周期性は空間格子によって表されるが、まず一次元の周期性から考えてみると、a軸上に同一図形が並んでいる例がわかりやすい。図形内に任意の1点(格子点)をとり、それと同価の隣の図形内の格子点と順次結んでいくと、a軸上に距離aの間隔を置いた点の配列ができる。図形のどこに点を設定してもaの値に変わりはない。この点の配列を一次元格子、aをその基本周期という。次に一次元格子を等間隔で平行に並べると二次元格子ができる。二次元格子は、a軸の基本周期a、b軸の基本周期b、およびab両軸のつくる角γで規定される。このときbの値はなるべく小さくなるよう設定する。二次元格子を等間隔で平行に積み上げれば三次元格子ができる。これが空間格子(結晶格子)である。空間格子は、3辺の長さがa、b、c、それらの間でつくる角α、β、γで規定される平行六面体を一単位とし、これを各軸に沿って平行移動させればつくられる。この平行六面体が単位格子(単位胞)である。このとき、a、b、cはなるべく短く、α、β、γは90度あるいはなるべく90度に近い値となるよう設定するのが普通である。
空間格子の格子点を任意に選んで平面(格子面)をつくると、それと等間隔で平行な平面の組合せが得られる。それらの格子面は、結局すべての格子点を含むことになる。格子面はa、b、c軸をそれぞれかならずa/h,b/k,c/lの間隔でくぎっている。h、k、lは0を含む整数で、格子面のミラー指数Miller indicesとよばれる。ミラー指数が0となるときは、その軸を無限遠でくぎる、つまりその軸に対して平行な面である。格子面はミラー指数によって(hkl)の記号で示され、負の指数となる場合は(
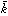
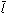 )のようにして示す。塩化ナトリウムを例にとると、純水溶液から成長した立方体の結晶には
)のようにして示す。塩化ナトリウムを例にとると、純水溶液から成長した立方体の結晶には
の各面が現れ、10%尿素水溶液から成長した正八面体の結晶には
の各面が現れている。格子面(hkl)の方向と面間隔は格子定数a、b、c、α、β、γによって定まるから、同一結晶であれば、晶癖のいかんにかかわらず、ある面と他の面とのなす角は一定になる。この関係は結晶外形の観察からすでに17世紀から面角一定の法則として知られていたが、結晶構造の詳細が判明している現在では、空間格子から必然的に導かれる自明の結果である。
[岩本振武 2015年8月19日]
対称と点群(晶族)
ある形をもつ物体をその物体を貫通する適当な軸の周りに回転させ、元の形と一致する(同位する)ことがあれば、その軸を回転軸という。すべての物体は360度回転させれば同位する。軸、鏡面、対称心などのように、それに基づいて物体の対称性を決めるものを対称要素、回転や鏡映、反転などの対称要素に基づいて行う操作を対称操作という。n回回転軸とは、(360/n)度の回転で同位する回転軸である。回転と反転とをあわせて行う操作を回反というが、ある物体を回転軸の周りで回転させ、ついでその軸上にある点について反転させれば同位するとき、その軸を回反軸という。1回回反軸は対称心の存在にほかならず、2回回反軸はその軸に直交する鏡面の存在にほかならない。反転とは、対称心を原点として、座標(x, y, z)の点を座標(-x, -y, -z)に移す操作で、鏡映とは、ある平面(鏡面)の手前にある点を鏡面と直交する直線上で等距離だけ反対側に移す操作である。結晶の外形に現れる特徴をその対称性からみると、結晶で独立に存在が許される対称要素は1、2、3、4、6回回転軸と1、2、4回回反軸の8種類だけであることが知られている。

これらのうち、5種の回転軸を本義回転軸、3種の回反軸を転義回転軸という。
結晶に現れる対称性は、これらおよびその適当な組合せ32種類であり、これを点群point groupまたは晶族という。群という用語は、これが数学の群公理を満足しているために使われている。点群はシェーンフリースの記号、あるいはヘルマン-モーガンの記号で表すが、結晶の対称要素が示されている後者のほうが便利である。
[岩本振武 2015年8月19日]
結晶系
単位格子の選び方には任意性があるが、a、b、cをなるべく短く、α、β、γを90度あるいはなるべく90度に近くなるよう設定すると、単位格子は形の特徴に従って7種類に分類できる。これを結晶系crystal systemという。結晶の空間格子は単位格子の平行移動によってつくられるから、前に述べたように結晶に許される回転軸が限定されるのである。簡単にするために二次元平面で考えると、同一図形で平面を空隙がなく埋め尽くすためには、正五角形や正八角形では不可能であり、正三角形、平行四辺形、正六角形などであれば可能となる。
[岩本振武 2015年8月19日]
ブラベ格子
空間格子の格子点はすべて等価である。ある単位格子を取り出し、その一頂点となる格子点を原点として結晶軸を設定したとき、残りの七頂点にある格子点も原点とまったく同じ幾何学的関係にある。このような格子点は、単位格子の八頂点のほかにも存在していることがある。単位格子内に平行六面体で、互いに平行な一組の面の中心にも存在するときは底心格子であり、3組の平行面のすべての中心にも存在するときは面心格子である。平行六面体の中心に存在するときは体心格子である。これらに対し、8個の格子点のみでつくられる格子を単純格子という。
7種の結晶系についてどのような格子が可能であるかは1850年フランスのブラベによって明らかにされ、14種しかありえないことが知られている。これをブラベ格子という。三方晶系には、単純菱面(りょうめん)体格子に対応するものと、単純六方格子に対応するものとがある。単純格子に対して、それ以外の格子を多重格子、体心および底心格子を二重格子(多重度2)または複格子、面心格子を四重格子(多重度4)という。底心格子を側面心格子ということもある。すべての格子について平行六面体の各頂点は等価である。
[岩本振武 2015年8月19日]
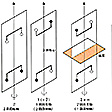
空間群
ブラベ格子の形がもつ対称性は、あくまで形そのものの対称性であり、単位格子内にどのように原子が配列しているかを示すわけではない。点群やブラベ格子は、周期性をもつ結晶構造のなかから、その単位となるものを取り出した、いわば孤立している構造を問題にしているが、結晶内では隣にも単位格子が存在している。そこで、隣の単位格子への平行移動を考えに入れると、新しい対称要素が発生する。それらは螺旋軸(らせんじく)と映進面である。螺旋軸は、回転とその軸に沿った平行移動の組合せである。また映進面は、鏡面での反射とその鏡面に沿った平行移動の組合せで、平行移動の距離は各周期の2分の1、いずれか二つの周期の和の2分の1(対角映進面)、あるいはいずれか二つの周期の和または差の4分の1もしくは三つの周期の和または差の4分の1(ダイヤモンド映進面)である。なお、回転+鏡映の対称操作を回映というが、1回回反軸は2回回映軸 、2回回反軸は1回回映軸
、2回回反軸は1回回映軸 と等しい。
と等しい。
結晶系、点群、ブラベ格子、螺旋軸、映進面の結晶構造において許される組合せは230種に限定され、それらのおのおのは数学的には群としての性質をもつため、空間群とよばれる。空間群がどのような対称要素をもつかは国際結晶学連合から刊行されるInternational Tables for Crystallography, Vol.Aに詳しく記載されている。空間群には同書での記載順に番号がつけられ、シェーンフリースの記号とヘルマン‐モーガンの記号が併記されている。シェーンフリースの記号は、対応する点群の記号の右肩に記載順の番号がつけられているだけであって、対称要素の説明には不十分なところがある。
ヘルマン‐モーガンの記号は、その空間群の基本となるブラベ格子の記号に続いて必要最低限度の対称要素が連記されており、空間群の内容を知るには便利である。結晶データの記載にはヘルマン‐モーガンの記号が一般に用いられている。
[岩本振武 2015年8月19日]
結晶の種類
結晶を構成する化学種が原子であるか、イオンであるか、分子であるかによって、あるいはどのような化学結合によって結晶がつくられているかを基準にして結晶を分類することができる。
[岩本振武 2015年8月19日]
金属結晶
単体の金属や合金は、原子が面心立方(立方最密)、六方最密、あるいは体心立方構造をつくった結晶構造をもつことが多い。各原子が提供する結合電子(価電子)は金属結晶全体に共有される金属結合をつくっている。結晶構造は一般に原子1個当りに金属結合で使われている電子の個数に依存しており、その数が1.5以下では体心立方構造、1.7~2.1では六方最密構造、2.5~3.2では面心立方(立方最密)構造となることが多い。
金属結晶では、原子一つ一つの間に方向性の定まった結合はないと考えられる場合が多く、たとえていうなら、金属結晶全体にわたる金属結合電子の海があり、そのなかに金属の原子(陽イオン)が島状に配置されているとみることができる。したがって、外力を加えると原子(陽イオン)の層が容易に移動し、延性(細長く伸びる性質)や展性(薄く広がる性質)を示す。
[岩本振武 2015年8月19日]
共有性結晶
結晶全体が方向性のある共有結合で連結された原子によって構成される結晶であり、ダイヤモンドがその典型的な例である。ダイヤモンドでは炭素原子がそれぞれ正四面体の頂点と中心を兼ねた位置を占め、1個の原子がそれぞれ4個の原子と結合した三次元無限連続構造をとる。すなわち一つの単結晶そのものが巨大な分子からなるものと考えられ、これらを巨大分子といっている。ケイ素、ゲルマニウムなどの14族元素の単体もダイヤモンド型構造をとる。結合電子数を原子1個当りで平均すれば4となる13族元素と15族元素との化合物、あるいは12族元素と16族元素との化合物も、ダイヤモンド型と同じような構造をつくることがある。共有性結晶は一般にきわめて硬く、ダイヤモンド以外でも、同型構造をとる窒化ホウ素はダイヤモンドよりも硬い。また、それらの融点もきわめて高い。しかし、結合の方向性が厳密なために延性や展性には乏しく、破断性の外力に対してはもろい。ケイ素、ゲルマニウムなどの14族元素の単体や、13族元素と15族元素との化合物(GaP, GaAsなど)は半導体として電子材料に利用される。
[岩本振武 2015年8月19日]
同素体
同じ元素の単体であっても、分子構造あるいは結晶構造の異なるものを同素体という。黒鉛はダイヤモンドと並ぶ炭素の同素体であるが、炭素原子間の共有結合では二次元の層状構造をつくる。原子1個は互いに他の3個と結合して正六角形状の網面をつくって二次元連続構造をとる。しかし、層間には直接の化学結合はなく、分子結晶と同じような分子間力だけが作用する。したがって、次に述べる分子結晶と考えることができる。窒化ホウ素にもダイヤモンド型とは別に黒鉛型構造をとるものがあり、これらは層間の分子間力が層内の共有結合に比べてはるかに弱いために、層間ではがれる劈開(へきかい)性や、層間のすべりによる潤滑性を示す。
[岩本振武 2015年8月19日]
分子結晶
もっとも簡単な分子は貴ガス(希ガス)にみられるような単原子分子であり、これらは主として面心立方構造の結晶をつくる。この種の結晶は分子間力で凝集するが、液体としての温度範囲がきわめて狭い特徴がある。多原子分子の結晶では、一般に分子量が大きいものは融点が高くなるが、分子の形や極性による影響も大きい。極性のある物質では、電気双極子モーメントによる静電的相互作用や水素結合も結晶の凝集力に寄与している。
[岩本振武 2015年8月19日]
イオン結晶
イオン結合によって生ずるのがイオン結晶である。融点は比較的高く、液体として存在する温度範囲も広い。見かけ上はイオン結晶と考えられる物質でも、その結合にかなり共有性をもつものもあり、それらは一次元、二次元、または三次元の連続構造をもつ共有性結晶に近い性質を示すことがある。
[岩本振武 2015年8月19日]
結晶成長
適当な溶媒と溶液をつくる物質の結晶は、その過飽和溶液から成長する。過飽和溶液は、溶解度の温度差を利用して高温度の飽和溶液を冷却するか、溶媒を常温で蒸発させれば得られる。これらの場合、冷却や蒸発の速度を小さくすると大きい単結晶を得ることも可能であるが、速度が大きいと小形の微結晶を得ることが多い。また、結晶成長の際に不純物や母液を取り込むこともある。このような場合にはそれらの結晶を取り出してもう一度溶液とし、再結晶を試みることが行われる。
固体が直接気体に変化することを昇華というが、逆に、気体が直接固体になることも昇華ということがある。固体を昇華させて得た気体を冷所に集めて結晶化させると良好な単結晶となることがある。無機化合物や金属塩は、融解物あるいは融解塩溶液からの結晶成長が単結晶製作法として実用化されている。結晶化すべき物質を融点よりやや高い温度の融体とし、真空または不活性気体の雰囲気中で種となる微結晶を融体に浸し、徐々に冷却しながら引き上げて結晶を成長させる単結晶引上げ法のほか、さまざまな方法があり、とくに高純度を必要とする電子材料の製法に応用されることが多い。雪の結晶にみられるような樹枝状に発達した結晶は、飽和溶液からの溶媒の蒸発によって得られることが多く、微細な単結晶が連結したものであるが、個々の単結晶は軸方向の整った良質の構造をもつものといわれている。
[岩本振武 2015年8月19日]
結晶の性質
結晶の性質は、それを構成している各原子あるいは分子そのものに由来するほか、それらの結晶内での相互位置の関係にもよることが多い。それらの結果として現れる異方性は、光学的性質としては、屈折率、光吸収係数、旋光度、偏光解消度などにみられる。電気的性質としては、導電率、誘電率、磁気的性質としては磁化率などがあり、また、機械的性質としては圧縮率、弾性率のほか、ある結晶面に沿ってはがれやすい劈開(へきかい)性がある。さらに比熱の温度変化のような熱的性質には、結晶内での分子の再配置や運動性なども関与する。結晶の構造とこれらの諸性質との関係は、物質の本性や化学結合性の理解のために重要な情報を与えるものとなっている。
[岩本振武 2015年8月19日]
人工宝石
錬金術は近代化学の発展によって否定されたが、ダイヤモンドのような高価な宝石の人工製造は高温高圧技術の進歩によって発展した。ダイヤモンドの化学組成が炭素にすぎないことが判明すると、多くの化学者がこれを人工合成しようと試みた。その最初は19世紀末のフランスのモアッサンやイギリスの無名の化学者ハネーらの試みであり、20世紀に入ってハーバード大学の物理学者ブリッジマンらの超高圧下での合成実験は超高圧物理学の格段の進歩をもたらしたが、いずれも科学的な意味でのダイヤモンド合成としては不成功に終わった。1956年アメリカのゼネラル・エレクトリック社は9万5000気圧、1600℃の条件下で合成に成功した。一方、ルビー、サファイアなどのコランダム系宝石の人工合成は比較的早く発展し、軸受、レコード針、装飾用などに多用されている。宝石は地球の進化に伴う高温高圧の特殊な条件下で天然に成長した結晶であるものが多く、そのような条件を人工的に設定できれば原理的には合成が可能である。
[岩本振武 2015年8月19日]
『仁田勇監修『X線結晶学』上下(1961・丸善)』▽『C・W・バン著、笹田義夫訳『化学結晶学』(1970・培風館)』▽『齊藤喜彦著『化学結晶学入門』(1975・共立出版)』

結晶、ガラス、液晶の相違
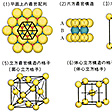
最密構造
塩化ナトリウムの結晶構造
結晶構造の周期性と単位胞

空間格子の格子面による分割

平面図形による対称要素の説明

結晶系と晶族

14種のブラベ格子
空間群の対称要素の比較

各種金属の室温における結晶構造

各結晶の特徴と代表的鉱物
百科事典マイペディア 「結晶」の意味・わかりやすい解説
結晶【けっしょう】
→関連項目完面像|結晶学|結晶光学|結晶格子|結晶水|固体|三斜晶系
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「結晶」の意味・わかりやすい解説
結晶
けっしょう
crystal
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
化学辞典 第2版 「結晶」の解説
結晶
ケッショウ
crystal
原子やイオンや分子が三次元に周期的に配列した空間格子をつくっている固体の状態.これが固体のもっとも安定な状態である.結晶の一般的な特徴は,方向によって原子配列が異なるため,種々の物理的,化学的性質に異方性が現れることである.結晶のなかには,結晶全体にわたって周期構造をもつ単結晶と,多くの微結晶がいろいろの方向をもって集合した多結晶とがある.単結晶は,一般にはっきりした結晶面をもち,多少とも対称的な外形をしているものが多く,鉱物がその代表的な例である.大部分の無機物,有機物も結晶化の条件によって単結晶になる.一方,金属や繊維などは多くの微結晶からなっていて,多結晶の代表例である.結晶以外の固体は無定形状態といわれるが,まったく周期構造をもたないということはなく,部分的には結晶に近い規則的な配列が存在している.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
岩石学辞典 「結晶」の解説
結晶
普及版 字通 「結晶」の読み・字形・画数・意味
【結晶】けつしよう
字通「結」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
栄養・生化学辞典 「結晶」の解説
結晶
世界大百科事典(旧版)内の結晶の言及
【固体】より
… この点で,バケツに入れた水がバケツの形に従うように,液体,気体の通性とはきわめて対照的である。
[結晶と非晶質]
固体では,それを構成する原子または分子は,固定した位置をもっている。この原子が空間的に規則正しく配列したものは結晶と呼ばれる。…
【双晶】より
…同一の種類の結晶の集合状態の一種。一つの種類の結晶ができるときには,遊離した個々の単結晶となる場合もあるが,多くは結晶個体が互いにくっつきあった集合体となる。…
※「結晶」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
1 食肉目クマ科の哺乳類の総称。全般に大形で、がっしりした体格をし、足の裏をかかとまで地面につけて歩く。ヨーロッパ・アジア・北アメリカおよび南アメリカ北部に分布し、ホッキョクグマ・マレーグマなど7種が...