線形写像（読み）センケイシャゾウ（その他表記）linear mapping

デジタル大辞泉

せんけい‐しゃぞう〔‐シヤザウ〕【線形写像】

ベクトル空間から別のベクトル空間への写像fで、次の二条件を満たすもの。f（a＋b）＝f（a）＋f（b）, f（λa）＝λf（a）（a、bはベクトル、λはスカラー）

出典　小学館

精選版 日本国語大辞典

せんけい‐しゃぞう‥シャザウ【線形写像】

1. 〘 名詞 〙 線形空間から線形空間への写像の一つ。線形空間Ｖから線形空間Ｗへの写像が次の条件を満たすとき、これをＶからＷへの線形写像という。(αa+βb)=α(a)+ β(b) （ただし、ａ、ｂはＶの元、α、βはスカラー）。一次変換。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

線形写像 (せんけいしゃぞう)
linear mapping

二次の正方行列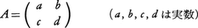，を一つ取り，平面のベクトル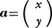，に対して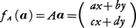，と定める。f_a（a）もまた平面のベクトルになるから，f_aは平面のベクトル全体の集合からそれ自身への写像である。ところで，任意のベクトルa，bと，任意のスカラーα，βについて，f_a（αa＋βb）＝αf_a（a）＋βf_a（b）となる。一般に体K上の線形空間V，W間の写像f：V→Wは，Vの任意の元a，bとKの任意の元α，βについて，f（αa＋βb）＝αf（a）＋βf（b）であるという性質をもつとき線形写像であるといわれる。線形写像f：V→Wについて，Ker（f）＝｛a∈V｜f（a）＝0｝，Im（f）＝｛f（a）｜a∈V｝はそれぞれV，Wの線形部分空間になる。Ker（f）をfの核，Im（f）をfの像と呼び，Im（f）の次元をfの階数という。V，Wがともに有限次元であるとして，e₁，……，e_nがVの，e₁′，……，e_m′がWの基底とすると，Vの元aは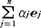と書ける。

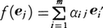と書けるから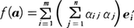，となる。このようにして，線形写像fは（m，n）行列（α_ij）に対応する。fの階数は行列（α_ij）の階数にほかならない。二つの線形写像f：U→V，g：V→Wの合成gf：U→Wも線形写像である。f，gがそれぞれ行列A，Bに対応すれば，gfは行列の積BAが対応する。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

線形写像
せんけいしゃぞう

平面を自分自身に写す写像fが、直線を直線に写し、原点を原点に写すとき、すなわち直交座標系に関して、
　　f(x,y)=(ax+by,cx+dy)
　　　(a,b,c,dは定数)
の形で表されるとき、fを平面の線形写像という。たとえば、原点の周りの角θの回転移動fは
　　f(x.y)
　　　=(cosθ・x-sinθ・y,
　　　sinθ・x+cosθ・y)
と表され、またx軸に関する対称移動gは
　　g(x,y)=(x,-y)
と表されるから、いずれも平面の線形写像である。しかし、平行移動は線形写像ではない。平面の線形写像は4個の定数a、b、c、dによって定まるので、これを2×2行列を用いて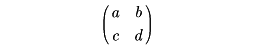

と表すのが普通である。同様に、空間を平面に写す線形写像、あるいは直線を自分自身に写す線形写像などが考えられる。たとえば、変数yが変数xに比例しているという関係はcを定数としてy=cxと書けるから、これは直線を直線に写す線形写像とみなせる。あるいは、空間ベクトルA=(a,b,c)を一つ定めておき、任意の空間ベクトルX=(x,y,z)にXとAの内積ax+by+cz=f(X)を対応させる写像fは、空間を直線に写す線形写像である。

　このように線形写像は、一つのベクトル空間Vをもう一つのベクトル空間Wに写す写像とみなすことができて、次のような性質をもっていることが、定義からすぐわかる。

（1）Vのすべての元X、Yに対して、
　　f(X+Y)=f(X)+f(Y)
（2）Vのすべての元Xとすべてのスカラーaに対して、
　　f(aX)=af(X)
これは、線形写像がベクトルの和とスカラー倍を変えないものであることを意味している。なお、ベクトル空間Vをベクトル空間Wに写す写像fが（1）、（2）の性質を満たすとき、fをVからWへの線形写像ということも多い。

［高木亮一］

[参照項目] | 一次変換 | ベクトル空間

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

線形写像
せんけいしゃぞう
linear mapping

ベクトル空間 V₁ から V₂ への写像 f：V₁→V₂ が次の2つの条件，すなわち，(1) V₁ の任意の元 x ，x′ に対して，f(x＋x′)＝f(x)＋f(x′) ，(2) λ をスカラーとするとき，V₁ の任意の元 x に対して f(λx)＝λf(x) を満たす f を線形写像 (1次写像) という。一般に，V₁ ，V₂ が有限次元であれば，これらの空間に基底を定めることによって，線形写像を行列で表現できる。線形写像の例は多いが，たとえばユークリッド空間における回転，裏返し，比例拡大などは，その空間におけるベクトルに線形写像を引起す。 (→1次変換 ) 　

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

線形写像【せんけいしゃぞう】

ベクトル空間Vからベクトル空間Wへの写像fが，Vの任意の要素x，yと任意の数aに対してf（x＋y）＝f（x）＋f（y），f（ax）＝af（x）をみたすとき，fをVからWへの線形写像という。代数学，位相数学で重要な概念。→線形／線形計画法
→関連項目写像

出典　株式会社平凡社