翻訳|length
精選版 日本国語大辞典 「長さ」の意味・読み・例文・類語
なが‐さ【長さ】
改訂新版 世界大百科事典 「長さ」の意味・わかりやすい解説
長さ (ながさ)
length
通常は長さとは先験的概念で線には長さが自然に備わっているとされている。数学でも18世紀まではそのように扱われてきたが,現在の数学では線の長さを厳密に定義する。長さのうちもっとも基本的なものは線分の長さである。公理的に扱うことによりこれに厳密な定義を与えることができるが,要するに線分の長さとは次のように定義される正の実数のことであるといえる。まず,一つの線分を選び,これを単位線分と呼ぶ。そして,任意に線分PQが与えられたとき,PQは単位線分の何倍であるかを調べ,はんぱがでればこれが単位線分の1/10の大きさの線分の何倍であるかを調べ,さらにはんぱがでればこれが単位線分の1/102の大きさの線分の何倍であるかを調べ,このことを限りなく続ける。このとき整数の列n,n1,n2,……が得られ,nは0,または正の整数で,n1,n2,……は0から9までの整数となる。そこでa=n+(n1/10)+(n2/102)+……とおき,これを線分PQの長さと定義する。空間に直交座標系が与えられ,P,Qの座標がそれぞれ(x1,x2,x3),(y1,y2,y3)ならば,線分PQの長さは, となるのである。
となるのである。
次に〈曲線の長さ〉を定義しよう。このため,曲線Cは,f,g,hを区間[a,b]で定義された連続関数として,x=f(t),y=g(t),z=h(t)(a≦t≦b)で表される直交座標(x,y,z)をもつ点の集合として与えられているとする。いま,[a,b]の任意の分割a=t0<t1<t2<……<tr-1<tr=bをとり,(f(ti),g(ti),h(ti))を座標にもつ点をPiとして(i=0,1,……,r),線分P0P1,P1P2, ……,Pr-1Prを作り,これらの線分の長さの和をlとする。このとき,[a,b]のすべての分割に関してlが有界ならば,Cは長さのある曲線といい,これらのlの上限をCの長さという。とくに,f,g,hが連続微分可能ならばCは長さのある曲線で,その長さは次の定積分で与えられる。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「長さ」の意味・わかりやすい解説
長さ
ながさ
length
平面内で考えたとき、重ね合わすことのできる二つの線分を、長さが等しいという。いま、ある一つの線分OEを固定して、これを単位として他の線分の長さを表す正の実数値を対応させる。このためには、の(1)のように、線分ABをOEの長さに等しく切っていき、余った部分は、OEをいくつかに等分したものを使って同様に測る。この操作を継続していく。これは、常識的な長さの測り方であるが、公理的構成の幾何学においては、この操作が可能であるように配慮して公理をつくっていかなければならない。ユークリッド幾何学では、ピタゴラスの定理(三平方の定理)が成立する。xy座標系の導入された平面においては、直交座標系により、A(a1,a2),B(b1,b2)の距離は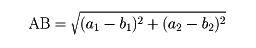
となる。これは、理論の構成の仕方により、他の定義から定理として導かれることもあり、またこれ自身を定義とすることもある。
[竹之内脩]
曲線の長さ
曲線L上に2点A、Bがあるとき、LのA、Bの間の長さは、次のように定める。L上、A、B間に数多くの点をとり、それらを順にP1,P2,……,Pn-1(A=P0,B=Pnとする)とする(の(2))。そして、これらの点を次々と線分で結んで折れ線をつくる。この折れ線の長さ(各線分の長さの和)が、この点のとり方を密にしていったとき、ある極限値に収束するならば、この曲線は長さがあるといい、この極限値を曲線のA、B間の長さという。曲線がx=f(t),y=g(t)で与えられているとき、曲線が長さをもつための条件は、f(t),g(t)がともに有界変動の関数であることである。とくに、曲線が滑らかな曲線であるとき、すなわち、f(t),g(t)がともにC1級関数(導関数が存在して連続であるような関数)であるときは、曲線は長さを有し、それは、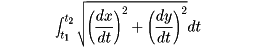
に等しい。ただし、t1、t2はA、Bに対応するパラメーターの値である。もしも曲線がy=F(x)の形で与えられているときは、長さを与える式は、
である。
[竹之内脩]
百科事典マイペディア 「長さ」の意味・わかりやすい解説
長さ【ながさ】
→関連項目求積法|体積|面積
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の長さの言及
【ユニタリ変換】より
…U*U=UU*=1(単位行列)なる正方行列Uをユニタリ行列といい,ユニタリ行列で表されるCnの一次変換φをユニタリ変換という。Cnの二つのベクトル,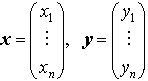 に対して,
に対して,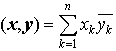 をxとyとの内積といい,また,
をxとyとの内積といい,また,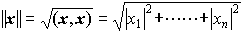 をxの長さという。ユニタリ変換φは内積および長さを不変にする。…
をxの長さという。ユニタリ変換φは内積および長さを不変にする。…
※「長さ」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
ローマ法王ともいう。ラテン語 Papaの称号はカトリック教会首長としてのローマ司教 (教皇) 以外の司教らにも適用されていたが,1073年以後教皇専用となった。使徒ペテロの後継者としてキリスト自身の定...



