非ユークリッド幾何学（読み）ヒユークリッドキカガク（英語表記）non-Euclidean geometry

デジタル大辞泉

ひ‐ユークリッドきかがく【非ユークリッド幾何学】

ユークリッド幾何学の平行線公理を、他の公理に置き換えて体系化した幾何学。ボヤイ＝ロバチェフスキー幾何学（双曲幾何学）・リーマン幾何学（楕円幾何学）など。これによれば、一直線外の一点を通りこれに平行な直線は1本とは限らず、三角形の内角の和は二直角にはならない。

出典　小学館

精選版 日本国語大辞典

ひ‐ユークリッドきかがく【非ユークリッド幾何学】

1. 〘 名詞 〙 ( ユークリッドは[英語] Euclid ) ユークリッド幾何学における平行線の公理を他の公理で置き換えて体系化された幾何学。置き換える公理によって、ボヤイ‐ロバチェフスキーの幾何学とリーマンの幾何学との二種が成立する。
   1. [初出の実例]「非ユークリッド幾何学の出発点が如何に常識的にをかしく思はれても」(出典：相対性原理側面観（1922）〈寺田寅彦〉)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

非ユークリッド幾何学 (ひユークリッドきかがく)
non-Euclidean geometry

〈平面上で，直線外の1点を通って，この直線と交わらない直線はただ一つ存在する〉という，いわゆる平行線公理が成り立つ幾何学をユークリッド幾何学と呼ぶ。これに対し，平行線公理が成り立たないような幾何学を非ユークリッド幾何学という。ユークリッド幾何学は前300年ころに書かれたユークリッドの《ストイケイア》によって確立されたが，非ユークリッド幾何学の誕生は19世紀においてであり，その間には長い苦渋の歴史があった。次に，その歴史を追いながら，非ユークリッド幾何学について述べよう。

　《ストイケイア》は，図形の性質の間にある論理的関係に注目して，それまでに知られていた図形に関する知識を一つの学問体系に組織立てたものであるが，そこでは議論を進めるための出発点として，まず点や直線などの定義を与え，続いて図形の基本的性質を5個の公準（要請）として述べ，また量の相等などについての9個の公理（共通概念）を述べている。このうち初めの四つの公準や九つの公理は，例えば〈任意の2点を直線で結ぶことができる〉のように自明の理と思われるものである。ところが，第5公準は〈2直線が1直線と交わっているとき，もし同じ側にある内角の和が2直角より小ならば，これらの2直線は限りなく延長すれば必ずその側で交わる〉と述べられていて，他のものに比べ内容も表現もはるかに複雑である。このために第5公準は後世の学者の批判の対象となり，これをより単純なものにおきかえようとする試みや，それを他の公準から証明しようとする試みが数多くなされた。そして，第5公準は平行線の公理や〈三角形の内角の和は2直角に等しい〉という命題と同値であることが認識されたのであるが，第5公準を証明しようという研究はすべて失敗した。この中にあって，G.サッケリは背理法による証明を試み，平行線公理が成立しないとの仮定のうえに立って，それに伴う種々の結果を導き先駆的業績をあげたが，彼もユークリッド幾何学は唯一の真理であるという思想から完全に脱却できず，非ユークリッド幾何学の発見者になれなかった。

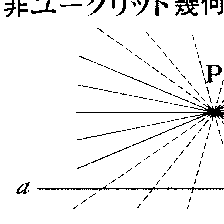
　19世紀になると，〈第5公準は成り立たなくてもよいのではないか〉〈直線外の1点を通ってその直線に平行な直線は二つあると仮定してもよいのではないか〉と考えられ始めた。この時代の最大の数学者C.F.ガウスもこのような考えをもち，かなりの成果を得ていたが，当時一世をふうびしたカント哲学の影響もあって，その研究を発表しなかった。第5公準以外の公準および公理はそのまま残し，第5公準に代わって〈平面上で，直線外の1点を通って，この直線と交わらない直線は少なくとも二つ存在する〉という公準を採用して，一つの幾何学を作り，勇敢にもそれを発表して，非ユークリッド幾何学発見の栄誉を得たのはN.I.ロバチェフスキーとボーヤイJ.で，それは1830年ころのことであった。この幾何学では，ユークリッド幾何学とはまったく趣を異にする次の定理が成り立つ。（1）1直線aとその上にない点Pが与えられたとき，Pを通る直線の集りは二つの組に分かれ，一方の組に属する直線（図1の点線）はいずれもaと交わり，他の組に属する直線（図1の実線）はaと交わらない。（2）三角形の内角の和は2直角より小さい。（3）対応する三つの角がそれぞれ等しい二つの三角形は合同である。B.リーマンのゲッティンゲン大学就任講演《幾何学の基礎にある仮説について》（1854）は幾何学に大革新をもたらし，それよりいわゆるリーマン幾何学が生まれたが，この幾何学の特別の場合として，リーマンは上述の非ユークリッド幾何学と別種の非ユークリッド幾何学を構成した。この幾何学では，平行線公理に代わって，〈平面上で，直線外の1点を通って，この直線と交わらない直線は存在しない〉が成り立ち，また，三角形の内角の和は2直角より大となる。さらに，直線は有限で閉じたものとなり，直線上の点の間の順序についてもユークリッド幾何学の場合と相違する性質がみられる。先に述べた非ユークリッド幾何学を双曲幾何学と呼び，この幾何学を楕円幾何学という。これらに対応してユークリッド幾何学は放物幾何学と呼ばれる。

　19世紀の終りころには，非ユークリッド幾何学のモデルをユークリッド幾何学の中に作るという仕事がE.ゲーリー，F.クライン，E.ベルトラミ，H.ポアンカレらによってなされた。例えば，ポアンカレが《科学と仮説》（1902）に記述しているモデルは次のようである。平面上に直線lをとり，lの上側にある半平面をHとして，次の擬用語を用意する。点とはHの点のことであり，直線とはlと直交する円または直線のうちH内にある半円または半直線のことであるとする。角はふつうの意味での角とし，点Aと点Bの間の距離を，図2のようにS，Tをとって，おのおのの場合に応じて，（AT×BS）/（AS×BT），BS/AS，AT/BTの対数として定義する。このようにするとき，これらの擬用語に関して双曲幾何学が成り立つ（図3）。ユークリッド幾何学の中に非ユークリッド幾何学のモデルが存在することは，ユークリッド幾何学の体系に矛盾がないかぎり，非ユークリッド幾何学の体系も無矛盾であること，したがって形式的な演繹体系とみるかぎり，ユークリッド幾何学と非ユークリッド幾何学は両立しうることを示している。なお，現実の時空はユークリッド的か，または非ユークリッド的かは物理学上の問題であるが，A.アインシュタインの相対性理論は後者と考えるほうが合理的であることを示している。
→幾何学
執筆者：中岡 稔

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

非ユークリッド幾何学【ひユークリッドきかがく】

ユークリッド幾何学の諸公理・公準のうち平行線公理だけを他の公理でおきかえて得られる幾何学。一直線外の一点を通りそれに平行な直線が無数に存在するとするボーヤイとロバチェフスキーの双曲的非ユークリッド幾何学と，平行な直線が１本も存在しないとするリーマンの楕円的非ユークリッド幾何学がある。前者では三角形の内角の和は２直角より小さく，後者では２直角より大きい。
→関連項目幾何学｜球面幾何学｜空間（哲学）｜空間（数学）｜公理｜射影幾何学｜数学｜平行｜ボーヤイ｜ロバチェフスキー

出典　株式会社平凡社

世界大百科事典（旧版）内の非ユークリッド幾何学の言及

【幾何学】より

…これを継承して，シュタイナーJ.Steiner(1796‐1863)は二次曲線や二次曲面も射影的に扱えることを示し，A.F.メービウスやJ.プリュッカーは座標を導入して射影幾何学を解析幾何学として建設し，またシュタウトK.G.C.von Staudt(1798‐1867)はデザルグの定理を基としてそれを総合幾何学として建設した。
［非ユークリッド幾何学］
　ユークリッドがあげた5個の公準のうち，第5番目のものは〈1直線が2直線と交わり，同じ側の内角の和が2直角より小ならば，2直線は限りなく延長するとその側で交わる〉と述べられている。この公準は他の公準に比べてすこぶる複雑で，その自明性に疑いがもたれた。…

【空間】より

…それは，空間関係を表現するための幾何学の多元性が認められたことである。空間関係は，ギリシア以来ユークリッドの幾何学によって一義的に記述されると考えられてきたが，19世紀に至って，非ユークリッド幾何学が出現して，空間関係の記述方法が幾通りもありうることが明らかになった。このことがのちに20世紀に入ってもう一つの空間概念の大きな変革を支えることになった。…

【数学】より

…上の仮定のもとでは三角形の内角の和は2直角より小さくなるが，球面幾何学と多くの類似点をもつ幾何学が構成されることが示されたのである。このように平行線の公理を否定した命題を仮定した幾何学を非ユークリッド幾何学といい，それに対して《ストイケイア》に見られるような幾何学をユークリッド幾何学という。ガウス自身大きな三角形について実測し，その内角の和と2直角との差を調べたが，それは誤差の範囲内にあって，現象空間でどちらの幾何学が成り立つかについての結論は得られなかった。…

※「非ユークリッド幾何学」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」