日本大百科全書(ニッポニカ) 「ポアズイユの法則」の意味・わかりやすい解説
ポアズイユの法則
ぽあずいゆのほうそく
Poiseuille's law
細い円管を流れる流体の量は管の両端の圧力差と管の半径の4乗に比例し、管の長さと流体の粘性に逆比例するという法則。1839年にドイツの水理工学者ハーゲンGotthilf Hagen(1797―1884)と、続いて40年にフランスの医師・物理学者ポアズイユJean L. M. Poiseuille(1799―1869)によって独立に実験的にみいだされたので、ハーゲン‐ポアズイユの法則ともいう。理論的には単位時間の流量Qは(π/8)・(p1-p2)a4/(ηl)で与えられる(p1-p2は管の両端の圧力差、lは管の長さ、aは半径、ηは粘性率)。この法則は粘性率の測定の基礎となる。流れのレイノルズ数R=ρUd/η(ρは密度、d=2aは管の直径、Uは平均流速:流量/管の断面積)が約2000以上の場合(たとえば太い円管)には流れは乱流となり、この法則は成り立たない。
[今井 功]
ブリタニカ国際大百科事典 小項目事典 「ポアズイユの法則」の意味・わかりやすい解説
ポアズイユの法則
ポアズイユのほうそく
Poiseuille's law
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
法則の辞典 「ポアズイユの法則」の解説
ポアズイユの法則【Poiseuille's law】
化学辞典 第2版 「ポアズイユの法則」の解説
ポアズイユの法則
ポアズイユノホウソク
Poiseuille's law
気体や液体などの流体が細管中を流れるとき,その流体の粘度ηは次式で与えられる.
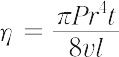
ここで,rは管の半径,lは管の長さ,Pは流体を流すために要する圧力,vはt時間に流れる流体の体積である.J.L.M. Poiseuille(1844年)が見いだした法則.この法則が成り立つためには,
(1)管が十分に細く,流体が管内を層流として流れること,
(2)流速は十分小さく,管の出口までに流体が得る運動のエネルギーが無視できるほど小さいこと,
を要する.流体の粘度測定法の原理として広く用いられる.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
改訂新版 世界大百科事典 「ポアズイユの法則」の意味・わかりやすい解説
ポアズイユの法則 (ポアズイユのほうそく)
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
世界大百科事典(旧版)内のポアズイユの法則の言及
【ハーゲン=ポアズイユの法則】より
…ポアズイユの法則ともいう。細いまっすぐな円管の両端に圧力差を与えたときの流体の流量を支配する法則。…
※「ポアズイユの法則」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
[名](スル)二つ以上のものが並び立つこと。「立候補者が―する」「―政権」[類語]両立・併存・同居・共存・並立・鼎立ていりつ...

