精選版 日本国語大辞典 「乗法」の意味・読み・例文・類語
日本大百科全書(ニッポニカ) 「乗法」の意味・わかりやすい解説
乗法
じょうほう
掛け算のこと。二つの数a、bが与えられたとき、aを1単位としてb単位にあたる数を求めるには、aにbを掛けるa×bを計算すればよい。この計算が乗法である。このとき、aを被乗数、bを乗数、a×bの結果を積という。bが正の整数のときは、a×bは、aをb回加え合わせることと一致する。乗法では、交換法則a×b=b×a、結合法則(a×b)×c=a×(b×c)が成り立ち、さらに、加法と関連して、分配法則a×(b+c)=a×b+a×cが成り立つ。また、数1は、どんな数aに対してもa×1=aとなる。一方、数0ではa×0=0となる。
整数の乗法の計算では、九九(乗法九九)が基本になる。これは、1桁(けた)の整数どうしとその積を1×1=1から9×9=81までを、被乗数に従って整理したものといえる。現在は、あらゆる組合せ(81通り)を含める(これを総九九という)が、大正期までは、先に唱える数が後に唱える数以下の場合(45通り)だけを考えた(これを制限九九または半九九という)。2数の少なくとも一方が2桁以上のとき、その積は九九と分配法則などの計算法則を用いて求められる。分数どうしの乗法では、分母の積を分母とし、分子の積を分子とする分数をつくればよい。負の数を含む数の乗法では、2数の絶対値の積に、符号の規則(同符号の2数のとき正、異符号の2数のとき負)によって定まる符号をつければよい。無理数を含む数の乗法では、その無理数に収束する有理数列をとり、それらの各項の積がつくる有理数列の極限値をとればよい。とくに、累乗根については、a>0, b>0のとき、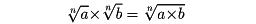
が成り立つ。複素数についても乗法が定められる。
(a+bi)×(c+di)=(ac-bd)+(ad+bc)i
(i=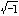 )
)
のように定める。文字式について乗法が定められる。数と文字との積は、3×a=a×3=3aのように、数を先に書き、記号×が省略される。文字と文字の積でも、同じように、a×bはabとして×は省かれる。単項式どうしの乗法では、数どうし、文字どうしを掛け合わせればよい。このとき、同じ文字の積は、a×a=a2, a×a×a=a3のように、累乗の形に書く。多項式の乗法では、分配法則A(B+C)=AB+ACによって、単項式どうしの積の計算に帰着させればよい。
[三輪辰郎]
ブリタニカ国際大百科事典 小項目事典 「乗法」の意味・わかりやすい解説
乗法
じょうほう
multiplication
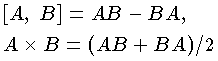 のような特殊な乗法を考えることもある。
のような特殊な乗法を考えることもある。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
改訂新版 世界大百科事典 「乗法」の意味・わかりやすい解説
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
世界大百科事典(旧版)内の乗法の言及
【四則】より
…分数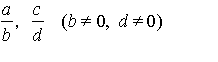 の間では,次のような演算ができる。
の間では,次のような演算ができる。 この和,差,積,商を得る4種類の基本的演算,加法,減法,乗法,除法を四則演算という。ただし,除法では0で割ることは考えない。…
この和,差,積,商を得る4種類の基本的演算,加法,減法,乗法,除法を四則演算という。ただし,除法では0で割ることは考えない。…
※「乗法」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
今日のキーワード
一富士二鷹三茄子
初夢に見るものの中で、縁起のよいとされているものを順に挙げた句。[補説]一に富士山、二に愛鷹あしたか山、三に初茄子の値段と、駿河国で高いものを並べた句ともいわれる。...
お知らせ
12/17 日本大百科全書(ニッポニカ)を更新
11/21 日本大百科全書(ニッポニカ)を更新
10/29 小学館の図鑑NEO[新版]動物を追加
10/22 デジタル大辞泉を更新
10/22 デジタル大辞泉プラスを更新
