応力（読み）オウリョク（英語表記）stress

デジタル大辞泉

おう‐りょく【応力】

物体が外力を受けたとき、それに応じて内部に現れる抵抗力。物体内部に任意の単位面積を考え、その両側が互いに及ぼし合う力の大きさと方向で表す。内力。歪力わいりょく。

出典　小学館

精選版 日本国語大辞典

おう‐りょく【応力】

1. 〘 名詞 〙 物体内に存在する内力。物体内に考えた面を両側から互いに押し合っている場合を圧力、引き合っている場合を張力、その面の両側を互いにずらすような場合をずれ応力という。内力。ストレス。⇔外力。〔工学字彙（1886）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

応力 (おうりょく)
stress

物体に外部から力が作用するとき，その反作用として物体内に生ずる分布内力を応力という。応力の大きさは単位面積に作用する内力の大きさにより定義され，これを応力度あるいは応力強さともいうが，一般には応力度のことを単に応力と呼び，以下の解説でも応力という場合は単位面積当りの応力を指すことにする。したがって，応力の単位は〈力÷面積〉の次元をもちkgf/cm²，kgf/mm²が多く用いられ，英米などヤード・ポンド法の国ではpsi（ポンド毎平方インチ）が用いられる。国際単位系（SI）では，N/m²あるいはパスカル（Pa＝N/m²）を用いる。

　物体の最小構成単位を原子と考えるとき，原子は原子間力などの結合力によって互いに結合され物体中の平衡位置にある。物体に外力が作用すると原子の平衡位置に変位が生じ，これに伴って物体内のいたるところで結合力が変化する。この結合力の変化が分布内力すなわち応力となって現れる。また，このとき物体には外形の変化または大きさの変化が現れる。単位長さあるいは単位体積当りの変形量をひずみといい，応力とひずみの間には密接な関係がある（ひずみ）。

　応力は物体の変形や破壊に対する強さを表すのに必要な量で，材料力学では重要な概念の一つとなっている。材料は形や大きさによらない固有の強さをもっており，それを表すには力そのものよりも力の面密度，すなわち応力を用いるのが適切であると考えられるからである。応力の概念はレオナルド・ダ・ビンチのノートにもその萌芽が見られるが，本格的な発展はガリレイが《新科学講話》の中で提案したはりの強さの問題に始まる。この問題は一端を壁に固定した棒の他端に荷をつり下げたときの棒の曲りを求めることであり，その後約2世紀にわたり数理物理学の問題として多くの学者により研究され，材料力学の体系を形成するもととなった。この間にR.フックによる弾性の法則の発見，ケルビンによる内力の概念の確立などを経て，1820年にA.L.コーシーによって応力状態の概念が確立されたのである。

面の応力

図1のように大きさが等しく向きが反対の外力P₁，P₂が作用する物体中のa－a′に断面Aを仮想し，Aより右の部分のつり合いを考えると，この部分には外力P₁と大きさが等しく反対向きの力Q₁が作用していなければつり合わないはずである。同様にAの左側部分については，P₂と大きさが等しく向きが反対の力Q₂が作用している。すなわち，Q₁，Q₂は断面を通して，両側の物体部分が互いに相手に及ぼす力（内力という）であり，Q₁とQ₂はつり合っていなければならない。この内力Q₁，Q₂は，仮想断面A上のいたるところに分布作用している力（分布内力）の合力として現れると考えるべきものである。物体はA上のいたるところでつながっており，内力はAを仮想することにより初めて現れるものであるから，Aの右側に作用していると考える分布内力は，左側のそれとA上のいたるところで大きさが等しく反対向きのはずである。いいかえれば仮想断面の左側の物体に作用する分布内力と右側の物体に作用するそれは互いに作用反作用の関係にある。このことは物体内にどのような面を仮想しても同じである。仮想断面の面積をA，ここに作用する内力の大きさをQとすれば，Q/Aはこの断面の平均内力密度を与える。もし分布内力が断面上に一様に分布作用していれば，Q/Aはこの面の応力にほかならない。面の応力はベクトル量であり，その作用する方向は外力の方向と同じであるから，考える面に垂直であるとは限らない。面の応力を表面力あるいは合応力と呼ぶことがあり，表面力のうち面に垂直な成分を垂直応力といい，ふつうσで表し，一方，面に平行な成分はせん断応力といいτで表す（図2）。垂直応力が面を境として互いに引っ張り合う作用をしているときこれを引張応力，押し合うとき圧縮応力と呼ぶ。せん断応力は面を境としてその両側の物体をずらせる作用をする。

点の応力

物体中のある点Oを通る微小な面dAに作用する分布内力の合力をdQとすれば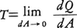，はO点において面dAに働く表面力である。dAの法線と表面力T（ベクトル）との交角をθとすれば，σ＝Tcosθ，τ＝Tsinθはそれぞれ点Oにおける面dAの垂直応力とせん断応力を与える。O点を通る他の面に作用する表面力は，一般にはTと等しいわけではなく，一つの面の表面力がわかっても別の面の表面力がわかるわけではない。ある点を通る任意の面の表面力が求められるのに必要な条件を点の応力あるいは応力状態という。この条件は，三次元の物体では，ある点を通りかつ互いに共通の交線をもたない3個の面の表面力が与えられることと等価である。そこで3軸直交座標系（x，y，z）を定め3個の基準面として座標面を用いることにする（図3）。ある点Oを原点とし，このまわりに3個の座標面とそれに平行な3個の面で作られる微小な直方体を考えて，x，y，z軸に垂直な各面に働く表面力T_x，T_y，T_zの座標成分を｛（σ_x，τ_xy，τ_xz），（τ_yx，σ_y，τ_yz），（τ_zx，τ_zy，σ_z）｝と書くと，この9個の成分がわかればよいことになる。この9個の応力成分の組を点の応力，あるいはコーシーの応力テンソルと呼んでいる。ここでσは垂直応力，τはせん断応力であり，σの指標は成分の作用方向（面の法線方向と同一）を，τの第1指標は面の法線方向，第2指標は成分の作用方向を示す。なお，せん断応力にはτ_xy＝τ_yx，τ_yz＝τ_zy，τ_zx＝τ_xzという性質があり，これを共役せん断応力の理という。垂直応力はこの直方体に引張りの作用をするときに正，圧縮のときに負の符号を与える。せん断応力はこのような作用別による区別がつかないので，直方体の面の外向き法線と成分の作用方向がともに座標軸の正または負方向であるとき正，それ以外のとき負の符号を与える。

　このように，ある点の応力は，3直交軸方向の三つの垂直応力成分と六つのせん断応力成分によって表されるが，直交する3平面の選び方によっては，その三つの平面上に作用する合応力がそれぞれの面に垂直となる。すなわち，このときには各面上のせん断応力成分は0となって，ある点の応力は三つの互いに直交する垂直応力だけで表せることになる。このような三つの垂直応力を，考えている点の主応力という。ある1点における主応力をσ₁，σ₂，σ₃としたとき，σ₁，σ₂，σ₃がいずれも0でない場合，その点は3軸応力状態にあるという。主応力成分のいずれか一つが0であるときは2軸応力（平面応力）状態，また主応力成分の二つが0のときを単軸応力状態という。

応力の現れ方

構造物や材料の強度を評価するにはその内部の応力分布を知る必要があり，このために応力解析を行う。応力解析には理論的，実験的，数値的な種々の方法がある。応力分布は物体の形や外力の性質により変わり，鋭い溝などのように形が急変する部分を切欠きというが，ここには周囲より大きい応力が発生する。これを応力集中といい，構造の破壊の主要な原因となる。

　実用の固体材料では外力が作用しなくても応力が発生していることがある。この応力を内部応力という。内部応力には，格子欠陥による原子配列の乱れに起因する微視的なものから構造全体に分布するものまであり，その発生機構によりさまざまな呼ばれ方がある。材料や構造物が製造された段階ですでに存在している内部応力を初期応力といい，これは製造過程で素材に加えられた無理がそのまま残ったものである。初期応力と似た概念である残留応力は，物体に加えられた外力が除去された後，物体内になお存在している内部応力を指す。溶接，熱処理などの過程により生じた内部応力も残留応力という。このほか外力の作用なしに発生する応力に熱応力がある。これは物体に温度分布があるとき熱膨張が不均一に生ずることにより発生するものである。残留応力はひび割れや応力腐食（応力の存在により腐食が促進される現象（応力腐食割れ））の原因となって材料や構造物を劣化させ，また熱応力は高温で使用される構造物の破損の原因となる。

応力の測定法

物体内で応力が一様に分布することがわかっている場合，例えば引張試験では物体に作用する外力を測れば，（外力）/（物体の断面積）で応力が求められる。応力分布があらかじめ予測できない場合には光弾性を利用した測定法が有効である。これはガラスやエポキシ樹脂などの材料に応力が作用しているとき，そこを通過する光の偏光面が回転する性質を利用したもので，光の干渉により生ずる干渉縞の分布から応力の分布や大きさを解析する。このほかX線の回折像から結晶の格子面間隔を測定し，これをもとに応力を算出する方法（実際はひずみを測定している），ひずみをひずみゲージで測定して，これから応力を求める方法などが利用され，また表面に塗料（応力塗料）を塗っておき，外力を加えたときに塗料の皮膜に生ずる亀裂から応力を求める方法もある。
執筆者：朝田 泰英

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

応力
おうりょく

物体に外から力を加えたとき、物体内部に仮想的な面を考えて物体を二つに分けて考えると、その面の両側は互いに力を及ぼし合っている。単位面積当りのこの力を応力という。この力の方向が面に垂直のとき法線応力、面に平行のときずり応力という。一般に斜めのときは、両方の成分があることになる。法線応力が互いに押し合う向きのとき圧力、引き合う向きのとき張力という。

　応力を定義するには、まず、面の方向（面の法線方向）を指定し、次のその面を通して及ぼし合う力の大きさと方向を与えなくてはならない。すなわち、応力は面の方向を示すベクトルと、力を示すベクトルとで与えられ、したがって、応力は2階のテンソルで表される。応力をTで表すと、x軸に垂直な面を考え、この面を通して及ぼし合う力のx、y、z成分をT_xx、T_xy、T_xzで表す。同様にT_yx、T_yy、T_yz、T_zx、T_zy、T_zzが考えられるが、力のモーメントがつり合っている条件としてT_yz＝T_zy、T_yx＝T_xy、T_xz＝T_zxでなくてはならない。したがって応力テンソルには一般にT_xx、T_yy、T_zz、T_yz、T_zx、T_xyの六つの独立な成分があり、全体として応力Tは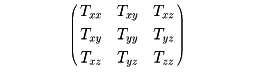

と書ける。このうちT_xx、T_yy、T_zzが法線応力（正のとき張力、負のとき圧力）の成分であり、T_yz、T_zx、T_xyがずり応力の成分である。xyz軸を適当に選ぶと、ずり応力成分がすべてゼロとなるようなxyz軸を探し出すことができる。このとき応力テンソルは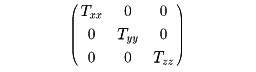

となる。このときのxyz軸を応力の主軸、T_xx、T_yy、T_zzを主応力という。流体中の静水圧の場合はT_xx＝T_yy＝T_zz＝－P（Pは静水圧）である。

［和田八三久・西　敏夫］

[参照項目] | ずり応力

応力（張力・圧力・ずり応力）

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

応力【おうりょく】

物体内部に考えた任意の単位面積を通し両側の部分が互いに及ぼしあう力。面に垂直な応力の成分を法線応力，面の接線方向の成分を接線応力という。また法線応力は面の両側の物体部分が互いに押し合うか引っ張り合う作用をもつので圧縮応力（圧力）または引張応力（張力）ともいい，接線応力は面に沿って両側の部分を相互にすべり動かそうとする作用（剪断作用）をもつので，剪断応力ともいう。→応力集中
→関連項目安全率｜許容応力｜クリープ｜クリープ試験｜剛性率｜降伏点｜材料力学｜ねじり試験

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

応力
おうりょく
stress

物体に外力が作用すると，物体内部にはもとの形状や寸法を保とうとする抵抗力（すなわち内力）が生じ，破断しないかぎり外力と釣り合っているはずである。この内力は，物体内に仮想する断面の取り方や断面上の位置によって変化する。内力 S が仮想断面（断面積 A）上で一様である場合は，S/A の値をもって応力あるいは応力度という。断面上で内力が変わるときには，ある位置の微小面積 ΔA に作用する内力 ΔS との比，すなわち ΔS/ΔA をとり，ΔA が 0に近づくときの極限値で定義する。仮想断面上に作用する応力の方向は，断面に対して常に垂直とはかぎらず，一般にはある傾きをもつ。したがって，この応力の断面に垂直な成分を垂直応力，断面に沿う成分を剪断応力，ずれ応力または接線応力と呼ぶ。前者で断面の外方向に向くときを引っ張り応力，断面に向かって押すように作用する場合を圧縮応力という。（→主応力）

出典　ブリタニカ国際大百科事典 小項目事典

岩石学辞典

応力

一般に物体の内部に考えた任意の単位面積を通して，その両側の物体部分が互いに相手に及ぼす力をその面に関する応力（stress）というが，応力にはいくつかの異なった定義がある．(1) 単位面積当たりの内部の力の強さで，物体の二つの隣接した部分の間にかかる作用と反作用をいう．ストレスは剪断応力（shearing stress）の接線成分，引張り応力（tensional stress），圧縮応力（compressional stress）などがある．(2) 外力が物体に働いた場合の物体の変形に対する抵抗で，ストレスは外力と等しい．(3) 静水圧によって保たれている平衡状態を不安定にする一方向の力．(4) 物体内部の任意の面の単位面積に働く力をいう．(5) 物体を変形する，または変形するように働く力をいい，単位面積当たりの力で測られる．ラテン語のstringereは引き合うの意味．

出典　朝倉書店

世界大百科事典（旧版）内の応力の言及

【音声学】より

…
【韻律的特徴】
　言語音声の強さ，高さ，長さをまとめて韻律的特徴prosodic featuresという。(1)強さアクセント(強弱アクセント)，あるいは強勢stressは音声を発する相対的な息の強さによる。英語では強勢に強[]と弱の別があり，その位置が自由に移動して語の意味を区別する。…

【ストレス】より

…ストレスは元来は機械工学的な用語で，物体を圧縮したり引き伸ばしたりしたときにその物体に生じる〈ひずみ〉を意味するが，1936年H.セリエによってストレス学説が提唱されて以来，この語はしだいに流布し，現今では日常用語化している。その邦訳語は〈負荷〉であるが，ほとんど用いられず，外来語のまま使用されている。
［ストレス学説］
　セリエは生体が外傷，中毒，寒冷，伝染病のような異なった種類の刺激にさらされた際，刺激の性格のいかんにかかわらず，ある種の一様な反応が生じる事実に注目した。…

【圧力】より

…一つの物体内でもその内部の各部分が互いに押し合っているときにはこれを圧力という。後者の場合には，物体内に面を考えてその両側の部分がこの面のところで互いに及ぼし合う力(応力という)として考える。これらの力が面に垂直でないときには，それを面に垂直な成分と平行な成分とに分け，垂直成分が押し合う力になっているときにこれを圧力という(引き合うときは張力)。…

【流れ】より

…　流体の中に任意の面をとると，両側の流体はその面をとおして互いに力を及ぼしあっている。これを応力といい，強さは単位面積当りの力で測る。静止しているふつうの流体では，応力は面に垂直で，互いにおしあう力(圧力)であって，その強さが面の方向によらない等方的な力である。…

※「応力」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」