粉砕（読み）フンサイ（その他表記）size reduction
comminution

デジタル大辞泉

ふん‐さい【粉砕】

［名］(スル)
１ こなごなに打ち砕くこと。「岩石を粉砕する」
２ 徹底的に打ちのめすこと。「敵を粉砕する」
[類語]撃破・破砕・討つ・打ち倒す・打ち破る・薙ぎ倒す・打ち負かす・打ち取る・打ち果たす・やっつける・倒す・打倒

出典　小学館

精選版 日本国語大辞典

ふん‐さい【粉砕・粉韲】

1. 〘 名詞 〙
2. ① 砕かれてこなごなになること。うちくだかれること。
   1. [初出の実例]「巖頭・雪峰等は、粉砕其身すとも、喫拳すべからず」(出典：正法眼蔵（1231‐53）仏向上事)
   2. [その他の文献]〔晉書‐郭璞伝〕
3. ② こなごなに砕くこと。転じて、相手、または敵を徹底的に打ち破ること。
   1. [初出の実例]「仇家を粉砕して去る」(出典：江戸繁昌記（1832‐36）三)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

粉砕 (ふんさい)
size reduction
comminution

固体粒子を砕いて細かくすること。鉱石，石炭，道路舗装材，コンクリート骨材，セメント原料，ガラス原料，セラミックス原料，製紙用粘土などの鉱物質原料をはじめ，われわれの日常生活に欠かせない穀類，塗料，薬品など，多くの物質を対象として粉砕が行われている。

　粉砕は主として固体粒子に対し，機械的な力を作用させることによって行われる。例えば，岩石をハンマーでたたくことによって粉砕することができる。あるいは，岩石を高所から硬い床の上に落としたり，硬い壁にぶつけることによっても，また硬い板の間に挟んで押しつぶすことによっても粉砕することができる。このように，機械力による粉砕では圧縮力，剪断（せんだん）力，衝撃力が使われる。粉砕装置によって，これらの力のどれが支配的であるかは異なっている。

　粉砕の対象物すなわち原料は，粒子径1m以上もある大塊から数十μmのものまで幅広く，また粉砕された粒子（粉砕産物）も粒子径10cm以上のものから1μm以下のものまでさまざまである。そこで慣習的に，比較的粗い粒子径の領域での粉砕を破砕crushing，比較的細かい粒子径の領域での粉砕を狭い意味で粉砕grindingと呼んで区別することがある。しかし破砕と狭義の粉砕との間に明確な境はない。

　物質を粉砕するためにはエネルギーが必要である。このエネルギーを粉砕エネルギーあるいは粉砕仕事という。選鉱工場，セメント工場などでは操業費の半分前後が粉砕工程に使われていることからもわかるように，鉱石やセメントのように大量の硬い粒子を粉砕するためには多くのエネルギーが必要である。また，比較的少量のセラミックス原料などでも，ごく細かく粉砕するためには，ひじょうに多くのエネルギーを必要とする。そこで粉砕エネルギーや粉砕エネルギー効率については古くから研究が行われてきた。粉砕エネルギーの実際的な評価には，粉砕機が消費した動力と，粉砕物の量および粒度との関係によってとらえる方法が一般的である。このような粉砕エネルギーの評価式としては，次の3者がよく知られている。

（1）リッティンガーの法則　リッティンガーP.von Rittingerが1867年に提案した粉砕エネルギーの評価式である。リッティンガーは粉砕に要するエネルギーは，粉砕の結果として新たに生成される粒子表面積の総和に比例すると考えた。球形粒子を想定するならば，粒子径dの粒子の表面積はπd²であり，その質量は（π/6）d³・δである（ただしδは粒子の密度）。したがって，単位質量当りの粒子の表面積の総和Sは，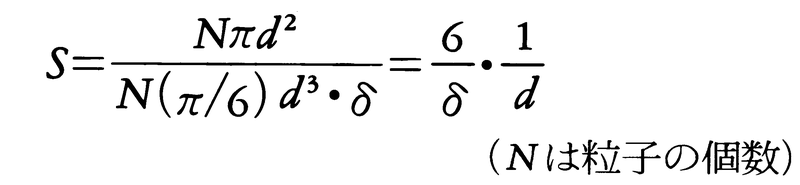

となり，均一な粒子径dをもつ粒子群の単位質量当りの表面積Sは粒子径dに反比例することがわかる。したがって，粉砕前後の粒子径をそれぞれd₁，d₂としてリッティンガーの法則を式で表すと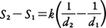，となり，この式から，単位質量当りの粉砕エネルギーWは，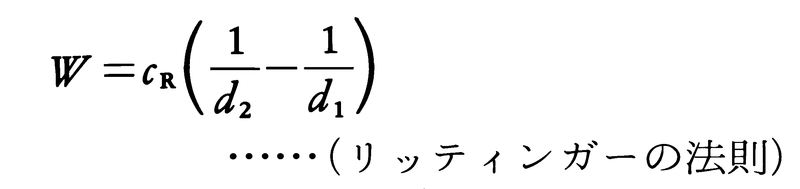

となる。ここでkおよびc_Rは比例定数である。新生表面積をその生成に要したエネルギーで割った値をcm²/kgf・cmの単位で表した数値はリッティンガー数と呼ばれ，その逆数は物質の粉砕抵抗の指標として使われている。なお一般に，新生表面の表面自由エネルギーは粉砕エネルギーの1%にも満たないことが知られている。

（2）キックの法則　キックF.Kickは1885年，ある物質の粉砕に必要な単位質量当りのエネルギーは粉砕前後の粒径比によって決まるという説を提唱した。この説はキックの法則と呼ばれる。単位質量粒子群を一定の粉砕比rでd₀→d₁→d₂→……→d_nのように粉砕したと想定すると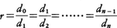，d₀からd_nにいたるn段の粉砕過程に対する粉砕比はrⁿであり，1段当りの粉砕エネルギーが一定値Eであったとすれば，粒径d₀からd_nへの粉砕に要するエネルギーWは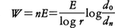，となる。仮定によりEとrは一定であるから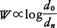，となる。d₀とd_nを改めてそれぞれd₁，d₂と書けば，が得られる。ここでc_Kは比例定数である。

（3）ボンドの法則　ボンドF.C.Bondは1952年，リッティンガーとキックの粉砕仕事法則に対し，粉砕の第3理論と銘打って次の考え方を提唱した。のちに修正されたボンドの説によれば，粒子の破壊に要するエネルギーは割れ目の長さの総和に比例し，したがって単位質量当りの仕事量としては，粒子径の平方根に反比例するというものである。すなわち，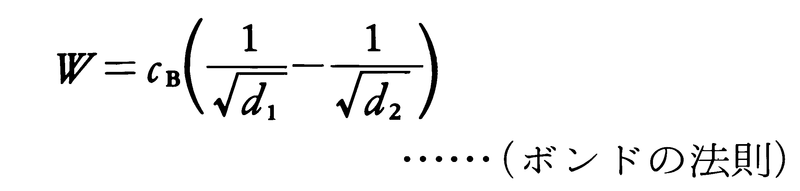

ここでc_Bは比例定数である。ボンドはこの式を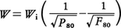，のように変形し，粉砕前後の80%通過粒度（粒度分布をもつ粉粒体に対し，その質量の80%が通過するふるい目の大きさ。転じて一般にその粒度以下の粒子質量割合が80%となる粒度）F₈₀およびP₈₀をそれぞれマイクロメートル（μm）で表し，原料1米トン当りの粉砕エネルギーをkWhで表した場合の比例定数W_iを仕事指数work indexと名付けた。仕事指数は，先に述べたリッティンガー数や後述のハードグローブ指数などとともに，原料の粉砕性を表す指標として有用であり，またボンドらが多数の鉱石および岩石類について，仕事指数の実測値を求めたところから，ボンドの式および仕事指数は粉砕機の設計や粉砕効率の評価などに広く使われるようになった。

　ある粉砕過程に対し，以上の三つの法則が同時に適合することはありえない。多くの経験からは粗粒域ではキックの法則，微粒域ではリッティンガーの法則が，それぞれ比較的よく適合するといわれている。粒度に対するエネルギーの関係において，両者の中間に位置するボンドの法則は，中間の粒度域をほどよくカバーしているともいえる。キックの法則は荷重下における粒子の変形と破壊の過程のうち，初期の弾性変形域を代表する仕事法則であり，リッティンガーの法則は後の破壊に伴う表面生成領域に着目した仕事法則となっている。したがって，新生表面積が大きい微粒域では，そのためのエネルギー消費が支配的となり，キック則からリッティンガー則への移行が見られるのではないかと思われる。ボンドの法則については理論的根拠がうすいと考えられる。なお数十μmから1μm以下の極微粉砕領域においては，リッティンガーの法則からもはずれ，粒径変化に対してさらに多くのエネルギーが必要とされるのがふつうである。これには材料の不均一性や粉砕機の粉砕効率の低下が原因になっていると考えられる。ある程度の粒度になると粉砕が実質上進行しなくなるところから，物質には粉砕限界が存在すると考えられた時期もあったが，粉砕方法によっては粉砕限界も上下することを考慮すると，粉砕限界説には今後修正が必要であろう。

　ローラーミルやボールミルなどにおける石炭の粉砕性を評価するために，しばしば使われている粉砕性評価指数として，ハードグローブ指数Hardgrove indexがある。これは所定質量，所定粒度の試料をボールレースミル（一種の小型ローラーミル）により標準の条件下で粉砕し，その粉砕産物を粒度分析することによって求められる。ハードグローブ指数の測定法を規定しているJIS　M8801では，質量50g，粒度1190～590μmの試料に対し，60回転（約4分間）の粉砕を行ったのち，74μmの試験ふるいによってふるい分け，その通過分質量W（g）より次式によってハードグローブ指数HGIを算出する。

　HGI＝13＋6.93W
執筆者：井上 外志雄

出典　株式会社平凡社「改訂新版　世界大百科事典」

化学辞典 第2版

粉砕
フンサイ
grinding

固体を細かく砕く操作をいう．固体の表面積を大きくして反応速度や溶解速度などを高めてプロセスの効率をよくする，多成分からなる鉱石を微細化して有用成分の分離をよくする，混合度を高め均一にしやすくする，などの目的で，化学工業，製錬工業などに広く行われている．粉砕には，衝撃，せん断，摩擦などが外力として用いられ，粉砕機としては，ボールミルやクラッシャーなどが代表的なものである．

出典　森北出版「化学辞典（第2版）」

百科事典マイペディア

粉砕【ふんさい】

固体物質の粒子を砕いて細かくする操作。粉砕の目的は，固体物質を所要の大きさにする（砂利，石炭など），表面積を増大させる（反応速度や溶解速度を高める），同一固体中の諸成分の分離を容易にする，各種固体原料の均一混合など。→粉砕機

出典　株式会社平凡社

栄養・生化学辞典

粉砕

　破砕と同じ意味に用いられる．物体をより小さな部分に分割すること．生成物が粉のように細かい場合，粉砕という．破砕は，水分含量の多いものなどに使う場合が多い．

出典　朝倉書店

普及版 字通

【粉砕】ふんさい

こなごなに砕く。

字通「粉」の項目を見る。

出典　平凡社「普及版 字通」

ブリタニカ国際大百科事典 小項目事典

粉砕
ふんさい

「破砕」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典