翻訳|random walk
改訂新版 世界大百科事典 「ランダムウオーク」の意味・わかりやすい解説
ランダムウォーク
random walk
乱歩または酔歩ともいう。酔っぱらいのふらふら歩きのように,左右どちらに進むか定まらない運動の確率論的モデルがランダムウォークXn(n=0,1,2,……)で,次のように定義される。ξn(n=1,2,……)をP(ξn=1)=p,P(ξn=-1)=1-pとなる独立確率変数とし,X0=a(aは整数),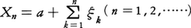 である。ランダムウォークはマルコフ系列の特殊なものであるが,賭の問題とも関連して古くからよく研究されてきた。
である。ランダムウォークはマルコフ系列の特殊なものであるが,賭の問題とも関連して古くからよく研究されてきた。
(1)l=(n+k)/2が整数のとき,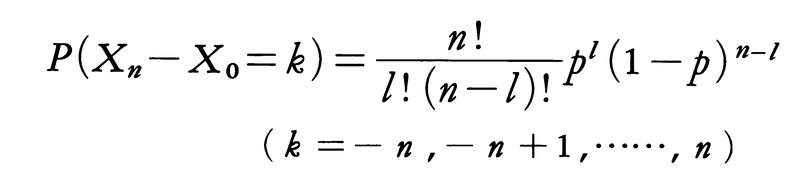
その他の場合,
P=(Xn-X0=k)=0
(2)ランダムウォークの出発点aを正の整数とし,τを0への到達時間とする。
q<pのとき,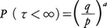
q≧pのとき,
P(τ<∞)=1
すなわち,負の偏りのあるランダムウォークは確実にいつか0に到達する。
(3)a=0,p=1/2の場合,
はn→∞のとき,一次元ブラウン運動に収束する。ここで[ ]はガウス記号でnt以下の最大整数を表す。
執筆者:西尾 真喜子
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「ランダムウオーク」の意味・わかりやすい解説
ランダム・ウォーク
らんだむうぉーく
random walk
無規則に動く粒子の運動のモデルで、乱歩、彷徨運動(ほうこううんどう)などとよばれることもある。例として、賭(か)けの問題での所持金の変動状況を表すもの、拡散粒子の運動の近似としての離散的記述などがよく知られている。これらのほかにも多種多様なモデルがあり、この考えは非常に広い応用範囲をもっている。ここでは、もっとも簡単な形の、以下のような例をあげる。
数直線上の整数の点だけを動く粒子を考え、初めにある点に位置する粒子が単位時間後に確率1/2で隣接する点(これは2個ある)へ移るものとする。この場合、粒子がいつかは初めの位置へ戻る確率は1であることが示される。
次に、同じ形の問題を二次元で考える。すなわち、平面上に座標を定め、二つの座標が整数であるような点だけを動く粒子を考え、初めにある点に位置する粒子が、単位時間後に確率1/4で隣接する点(これは4個ある)へ移るものとする。この場合、粒子がいつかは初めの位置へ戻る確率は一次元の場合と同じで1であることが示される。
次に同じ形の問題を三次元で考える。すなわち、空間に座標系を定め、三つの座標が整数であるような点だけを動く粒子を考え、初めにある点に位置する粒子は単位時間後に確率1/6で隣接する点(これは6個ある)へ移るものとする。この場合、粒子がいつかは初めの位置へ戻る確率は、一次元、二次元の場合と異なり、約0.35であることが示される。
以上の例では、どの隣接点へ移る確率も同じと考えたが、一般的には、各点pに対してその隣接点に移る確率(各隣接点ごとに異なってもよい)と点pにとどまる確率が与えられていて、しかもこれらの確率の値は点pによって異なってもよい、とするのである。このような一般の場合には一次元の場合でも「粒子がいつかはもとの位置に戻る確率は1」という性質は一般には成り立たない。
[古屋 茂]
『W・フェラー著、国沢清典監訳『確率論とその応用』(1970・紀伊國屋書店)』
世界大百科事典(旧版)内のランダムウオークの言及
【ブラウン運動】より
…時間tだけたつと微粒子がはじめの位置からrだけ離れたとして,r2の値をいろいろな微粒子について平均してみると,その値〈r2〉はtに比例していることが見いだされた。これはブラウン運動が数学上random walkと呼ばれる問題に帰着する証拠である。random walkはまた酔歩とも呼ばれ,これはまさに酔いすぎた男の足どりである。…
【確率過程】より
…ωを固定すると,Xt(ω)はtだけの関数になるが,これを見本関数とか標本関数などという。 例1 硬貨を次々と投げて,表が出たら1だけ右に進み,裏なら1だけ左に進む直線上の不規則運動をランダムウォークという。t回投げたとき,Xt(ω)=(表の出た回数)-(裏の出た回数)とおき,またX0=0とする。…
※「ランダムウオーク」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
今日のキーワード
イチロー
[1973~ ]プロ野球選手。愛知の生まれ。本名、鈴木一朗。平成3年(1991)オリックスに入団。平成6年(1994)、当時のプロ野球新記録となる1シーズン210安打を放ち首位打者となる。平成13年(...
お知らせ
12/17 日本大百科全書(ニッポニカ)を更新
11/21 日本大百科全書(ニッポニカ)を更新
10/29 小学館の図鑑NEO[新版]動物を追加
10/22 デジタル大辞泉を更新
10/22 デジタル大辞泉プラスを更新
