一般的にいえば判断とは〈何事かに関して真(または偽)と判ずるところの人間の心的作用〉を意味する。一方,命題propositionは論理学において通常〈その真偽に関して論じうる文(たとえば感嘆文や命令文は命題でない)〉と規定されており,したがって,命題は判断の言語表現であるといえる。ここでは論理学の用語としての〈判断〉について述べるが,論理学の対象として見るかぎりでは,判断と命題はとくに区別する必要はない。
(1)伝統的論理学においては,判断(命題)とは〈二つの概念の結合または分離(の叙述)〉である。すなわち,S,Pを概念(名辞)とするとき,もっとも基本的な判断(命題)は下記のものであるが,(1)においてはSにPが結合されており,(2)においてはSからPが分離されている。
(1) S is P SはPである
(2) S is not P SはPでない
したがって判断(命題)は概念(名辞)と推理(推論)とのいわば中間に位置する。なぜなら,概念(名辞の対象)と概念(名辞の対象)の関係の把握(叙述)が判断(命題)であり,かつ,判断(命題)と判断(命題)の関係の把握(叙述)が推理(推論)であるといえるからである。さて(1)ではSに対してPが肯定されているといわれ,(2)ではSに対してPが否定されているといわれる。そして(1)の型の命題(判断)は肯定命題(肯定判断),(2)は否定命題(否定判断)と呼ばれる。(1)においてSは主語subject,Pは述語predicateと呼ばれ,〈is(である)〉は二つの名辞(概念)をつなぐものとして繫(けい)辞またはコプラcopulaと呼ばれている。さて,まず主語Sが個体のとき,(1),(2)は単称命題といわれる。例えば〈ソクラテスは人間である〉は単称命題である。次に,主語Sが〈人間〉〈動物〉など事物の集り(集合)である場合,その範囲を明確にするため〈すべての〉〈或る〉などの限定詞がSに付加されることになる。したがって,これらの限定詞と肯定・否定の組合せから,次の4種類の命題の型が得られる。
(3) すべてのSはPである ……(A命題)
(4) 或るSはPである ……(I 命題)
(5) いかなるSもPでない ……(E命題)
(6) 或るSはPでない ……(O命題)
(3)と(5)は全称命題,(4)と(6)は特称命題と呼ばれる。したがって(3)は全称肯定命題と呼ばれるが,これはA命題と略称されている。同様に(4)は特称肯定命題=I命題,(5)は全称否定命題=E命題,(6)は特称否定命題=O命題と呼ばれている。略称のAとIはラテン語の FF
FF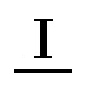 RMO(肯定する)から,EとOはN
RMO(肯定する)から,EとOはN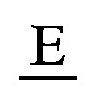 G
G (否定する)から由来する。以上,単称命題とA,I,E,Oの命題は,定言命題と総称されているが,伝統的論理学ではそのほかに次の命題の型が取り上げられている。p,qを任意の命題とするとき,(a)〈pならばq〉という命題は仮言命題と呼ばれ,(b)〈pまたはq〉は選言命題と呼ばれる。そしてこの両者(a)(b)は条件命題と総称されている。
(否定する)から由来する。以上,単称命題とA,I,E,Oの命題は,定言命題と総称されているが,伝統的論理学ではそのほかに次の命題の型が取り上げられている。p,qを任意の命題とするとき,(a)〈pならばq〉という命題は仮言命題と呼ばれ,(b)〈pまたはq〉は選言命題と呼ばれる。そしてこの両者(a)(b)は条件命題と総称されている。
→三段論法
(2)現代論理学では次の命題の型がもっとも基本的とされている(下記において,a,b,cとa1,a2,……,anは個体を,R1,R2,……,Rnは個体の集合または個体間のなんらかの関係を表すものとする)。
(1)ソクラテス(a)は人間(R1)である
(1′)aはR1に属する
(2)太郎(a)は花子(b)を愛する(R2)
(2′)aとbはR2という関係にある
(3)一郎(a)の両親(R3)は太郎(b)と花子(c)である
(3′)a,b,cはR3という関係にある
(4)a1,……,anはRnという関係にある
(n≧1)
(1)は(1′)の一例であり,同様に(2)は(2′)の,(3)は(3′)の一例である。したがって上のすべては(4)の例であると考えられる。(4)のRnはn項述語(またはn項関係)と呼ばれる。さて(4)の型の命題は単純命題と呼ばれるが,われわれはいくつかの単純命題をもとに〈……でない〉〈……または--〉〈……かつ--〉〈……ならば--〉〈すべての個体xについて……〉〈或る個体xについて……〉などの語句(これらは論理語と呼ばれる)を用いて,別の命題を合成することができる。合成によって生み出された命題は複合命題と呼ばれる。例えば次の(5)(6)は複合命題であり,おのおの(5′)(6′)の一例である。
(5)或る男性(R1)は花子(a)を愛する(R2)
(5′)或る個体xについて(xはR1に属し,かつ,xとaはR2の関係にある)
(6)すべての人間(R1)は動物(R1′)である
(6′)すべての個体xについて(xがR1に属するならば,xはR1′に属する)
以上から明らかなように,現代論理学での命題の定式化は伝統的論理学の命題形式をすべて含むことになる。例えば,上の(6′)は伝統的論理学でのA命題に相当する。
執筆者:岡部 満


 FF
FF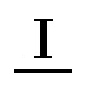 RMO(肯定する)から,EとOはN
RMO(肯定する)から,EとOはN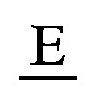 G
G (否定する)から由来する。以上,単称命題とA,I,E,Oの命題は,
(否定する)から由来する。以上,単称命題とA,I,E,Oの命題は,
 、~司徒
、~司徒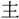
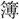 に任ぜられ、能く
に任ぜられ、能く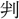 斷するを以て、時人に知らる。號して入鐵
斷するを以て、時人に知らる。號して入鐵