翻訳|matrix
精選版 日本国語大辞典 「行列」の意味・読み・例文・類語
ぎょう‐れつギャウ‥【行列】
日本大百科全書(ニッポニカ) 「行列」の意味・わかりやすい解説
行列
ぎょうれつ
matrix
m、nを自然数としてmn個の数aij(i=1, 2,……, m ; j=1, 2,……, n)を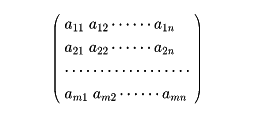
と並べたものをm×n型行列という。この型の行列の全体をMと記すことにする。たとえば、すべてのaijがゼロである行列はMの元であるが、とくに零行列とよばれてOと表される。
A、BをMの元、すなわちm×n型行列とする。AとBとの和A+Bを成分ごとの和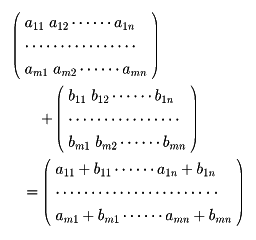
で定義する。
するとMはこの演算で閉じており、加群をなすことが、ごく簡単に示される。単位元はOである。次にcを数(スカラー)とし、cとAとの積cAを(i, j)成分がcaijなる行列として定義する。すなわち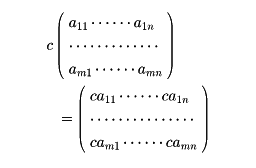
である。
最後に行列の積を定義するが、簡単のためmとnとが等しい場合、すなわちn次正方行列に限定する。AとBとの積ABの(i, j)成分を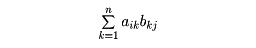
とする。すなわち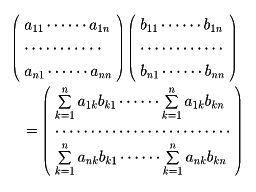
である。たとえばnが2のときを例にとると、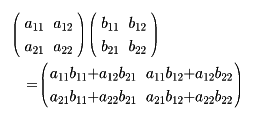
となる()。
A、B、Cをn次正方行列とすると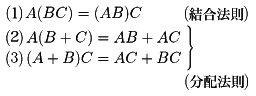
が成り立つ。なお一般には積に関しては可換法則AB=BAは成り立たないことは注意を要する。ただEを単位行列
とすると、AE=EA=Aが任意のn次正方行列Aに対して成り立つ。
以上を総合して、代数学の用語を使うならば、n次正方行列の全体は、単位元を有する非可換な環をなすことがわかる。
なお、m≠nの場合でも、Aがm×n型行列、Bがn×l型行列の場合、積ABが定義される。その方法は正方行列の場合に準ずる。
[足立恒雄]
連立一次方程式
行列の例として連立一次方程式を考える。次の連立一次方程式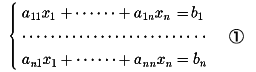
は、また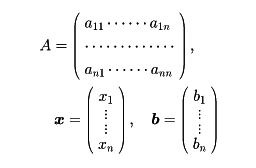
と置くとき
Ax=b ②
と表せる。このように行列を用いると、連立一次方程式の表示がきわめて簡単になる。
さて、ある正方行列Bが存在してBA=Eが成り立つものとすると(Eは単位行列)、②の両辺に左からBを掛けることによって
x=Bb
と解xが求められることになる。このようなBのことをAの逆行列といい、A-1と表す。逆行列はあるとしてもただ一つで、このときAA-1=A-1A=Eが成り立つ。逆行列の存在する正方行列を正則であるという。行列Aが正則である条件は、Aの行列式|A|がゼロでないことである。以上により、Aが正則なときは②、したがって①はただ1組の解をもち、それはA-1bと表される。
[足立恒雄]
掃き出し法
ここでは数値的に連立方程式を解く方法を述べる()。例として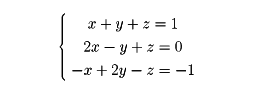
をとる。未知数と等号を略してのように記す。方程式の順序を入れ換えても解は変わらないから、の行列の行を入れ換えてもよい。また一つの方程式に一定の数を掛けて他の方程式に加えても解は変わらないから、一つの行を何倍かして他の行に加えてもよい。また一つの行にゼロでない数を掛けてもよいことが同様にわかる。列に関しては、最後の列以外の2列を入れ換えてもよいこと以外は許されない。これらの操作を繰り返して単純な形へと変形した過程がである。結果としてx=-1, y=0, z=2という解を得る。以上の解法が掃き出し法である。興味深いのは、行に関する三つの基本変形(行の入れ換え、一つの数を掛けて他の行に加える、ゼロでない数を一つの行に掛ける)が、特殊な正則行列を左から掛けることで表現できることである。で2×2行列の場合を例示してあるが、一般でも同様である。
[足立恒雄]
行列の階数
Aをm×n型行列とする。いま、行基本変形とともに列基本変形も許すとする。列基本変形は、行基本変形の行列をAに右から掛けることによって得られる。Aに行と列の基本変形を何回か行って、主対角線上に1が、他は0がくるようにする。最後に残った1の数をAの階数(ランク)という。Aがn次正方行列のとき、Aが正則である条件は、Aの階数がnとなることである。
[足立恒雄]
逆行列の求め方
n次正方行列Aが正則のときは、前項で記したように階数はnである。したがって施した行基本変形を掛け合わせてB、列基本変形を掛け合わせてCとするとBAC=Eとなる。両辺に左からC、右からC-1を掛けると
C(BAC)C-1=CEC-1=CC-1=E
ゆえに(CB)A=Eを得る。CBは行基本変形を何回か行う行列であるから、結局、行基本変形だけでAをEに変えることができる。またこのCBが逆行列である。いまXA=EとすればXE=Xだから、AをEに変える行変形をEに施せば、逆行列Xが得られることになる。これがの逆行列を求める原理である。
[足立恒雄]
行列と線形写像
V、Wをベクトル空間、TをVからWへの線形写像とする。すなわち、Vの任意の二つのベクトルx、yとスカラー(数)λに対して
T(x+y)=T(x)+T(y),
T(λx)=λT(x)
が満たされるとする。Tが上への一対一写像であるとき、Tは同形写像であるといわれる。同形写像が存在するとき、VとWは同形であるといわれる。また、V=Wのときは線形写像は線形変換といわれる。
n項縦ベクトルの全体Rnは代表的なベクトル空間である。いま、VがRnで、WがRmである場合を考える。Aを一つのm×n型行列とする。Vの縦ベクトルxに対して
Tx=Ax ③
でもって写像T : V―→Wを定義すれば、Tは線形写像である。ところが逆にTをVからWへの線形写像とすれば、③を満たすような行列Aがとれる。すなわち、縦ベクトルのなすベクトル空間の間の線形写像とは行列のことである。AをTに対応する行列という。RmとRnとはm=nのときに限り同形である。また正方行列Aが同形写像を与える条件は、Aの行列式|A|が0でないことである。このことは連立一次方程式②の解の存在の条件からもわかる。有限次元のベクトル空間は同一次元の縦ベクトルの空間に同形であるので、有限次元のベクトル空間の間の線形写像は、縦ベクトルのなす空間に移してみれば行列で表現される。これにより有限次元のベクトル空間の理論は行列の理論そのものであることになる。これが行列の概念を重要なものとする最大の理由である。
[足立恒雄]
一般の連立一次方程式
未知数の数と方程式の数とが一致するとは限らない場合を考える。
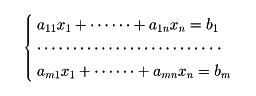
という連立一次方程式は、Aを係数のなすm×n型行列、xを未知数のなすn項縦ベクトル、bをb1、……、bmのなすm項縦ベクトルとすると
Ax=b ④
と表せる。ÃでもってAの右にbを並べたm×(n+1)型行列を表すことにする。
Ãに行基本変形とn+1列目以外の列の入れ換えとを行って得られる標準形が
であるとする(こういう形にかならず変形できる)。rはAの階数である。この行列を入れ換えた列の変数を付け換えて連立一次方程式に直してみると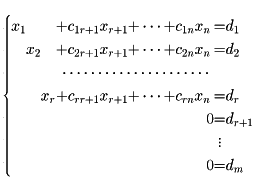
となる。したがって④が解をもつ条件は
dr+1=……=dm=0
すなわち、Aの階数とÃの階数が一致することである。そしてこの条件が満たされるとき、上の方程式の解は、ベクトルで表すと
x=λ1c1+……+λn-rcn-r+d
(λ1,……,λn-rは任意の数)
の形である。b1、……、bnがすべて0の場合、自明でない解、すなわちx1、……、xnがすべては0ではない解を有する条件はn>rである。とくにn>mつまり未知数の数が方程式の数より大きいならば(m≧rだから)つねに自明でない解を有することになる。
[足立恒雄]
『田島一郎著『新しい数学へのアプローチ4 線形代数』(1970・共立出版)』
改訂新版 世界大百科事典 「行列」の意味・わかりやすい解説
行列 (ぎょうれつ)
matrix
数や関数などを,長方形の形にまとめて括弧をつけたものを行列という。シルベスターJ.J.Sylvesterが1850年ごろ使い始めたもので,マトリックスmatrixと命名された。しかし,1845年のケーリーA.Cayleyの一次変換についての論文にすでにこの概念の萌芽があった。日本語訳は,母式,方列などを経て,高木貞治の命名による行列になった。括弧( )のほか,/ /,[ ]の記号が使われる。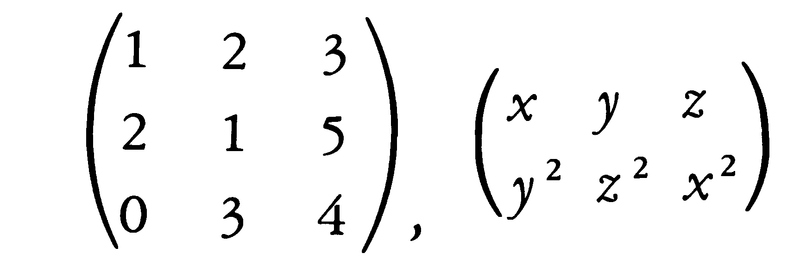
横向きの各列を行といい,上のほうから順次第1行,第2行,……と呼ぶ。縦向きの各列を列と呼び,左のほうから順次第1列,第2列,……と呼ぶ。行の数がm,列の数がnの行列をm行n列の行列,または(m,n)行列という。(n,n)行列をn次正方行列という。
並べられている数や関数を行列の成分という。(i,j)成分というときは,第i行の左からj番目の成分を指す。
成分がすべて実数であるとき実行列といい,成分がすべて複素数であるとき複素行列という。成分がすべて関数であっても関数行列とはいわない。すべての成分が0の行列をゼロ行列といい,0で表すのがふつうである。m,nが変われば別の行列であるが,同じ0で表しているので,取扱いには注意を要する。
行列の演算
行列には一次変換を対応させて考えることが多い。例えば,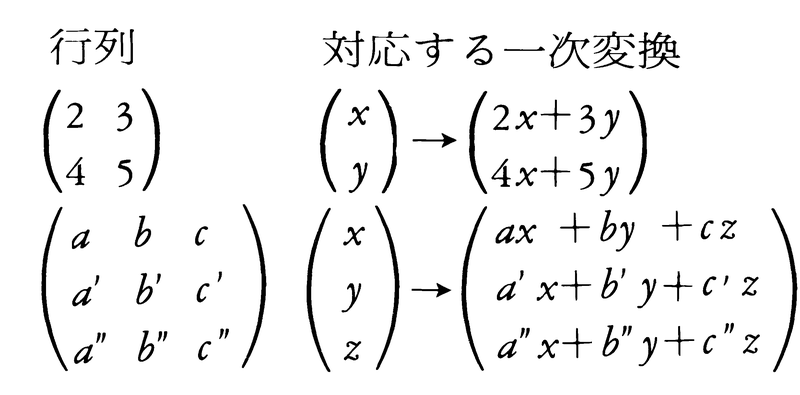
この対応がうまくいくように(例えば,一次変換の合成と行列の乗法とが対応するように),行列の演算を定めるのが便利であるという理由で,次のような3種の演算が定義されている。
(1)行列の加法 ベクトルと同様に,二つの(m,n)行列について,その和は対応する成分の和を成分とする行列と定める。例えば,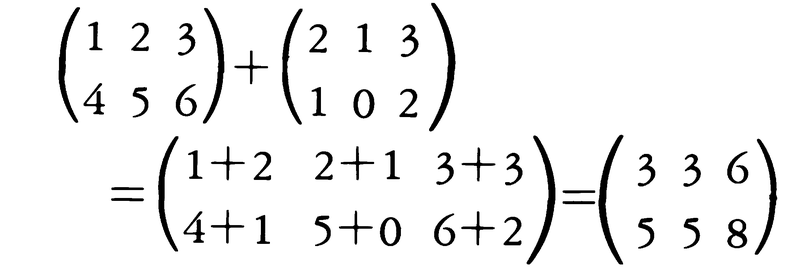
行数または列数の異なる行列の和は考えない。
(2)行列の積 二つの行列A,Bについて,Aの列の数とBの行の数とが等しいときに,積ABを定義する。まず,(Aの行の数)=(Bの列の数)=1のときは,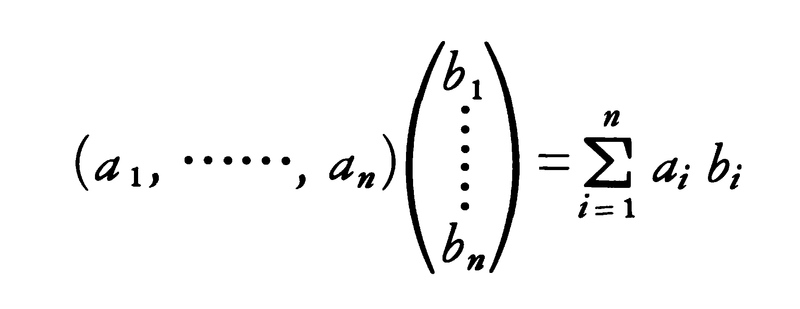
と定め,一般の場合は,ABの(i,j)成分は(Aの第i行)と(Bの第j列)の積と定める。例えば,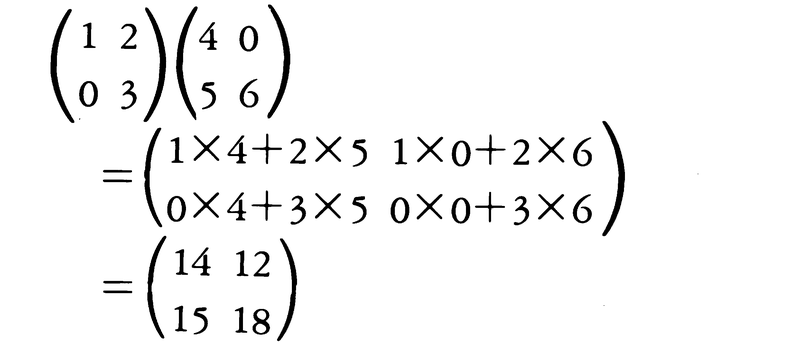
(m,n)行列Aと(n,k)行列Bとの積ABは(m,k)行列になる。n次正方行列についてのこの乗法において,群の乗法のときの単位元と同様の性質をもつのは各(i,i)成分が1で,他の成分がすべて0のもので,これをn次の単位行列という。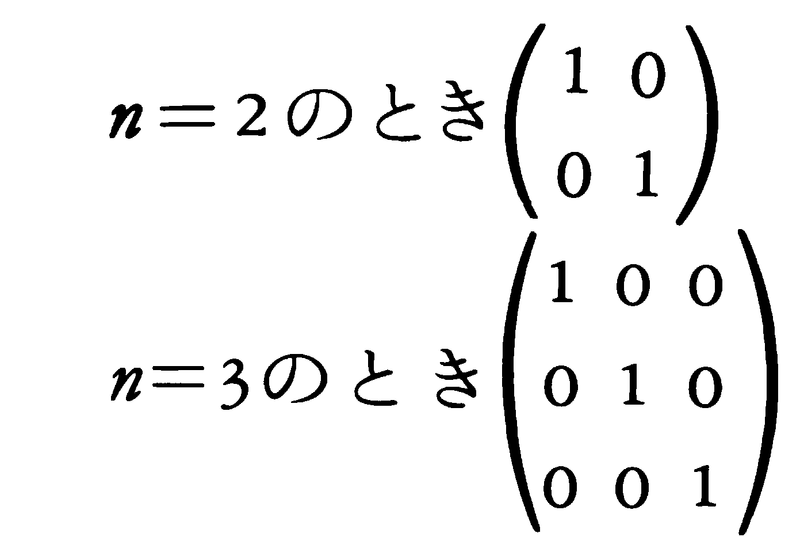
(3)行列のスカラー倍 行列に対して,数や関数をスカラーという。行列Aにスカラーcをかけた積は,Aのすべての成分にcをかけたものと定める。例えば,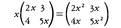 単位行列のスカラー倍,すなわち,(i,i)成分が一定で,他の成分が全部0のものをスカラー行列という。
単位行列のスカラー倍,すなわち,(i,i)成分が一定で,他の成分が全部0のものをスカラー行列という。
上の(2)で定めた乗法によれば,例えば,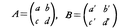 による一次変換は,
による一次変換は,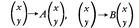 と書いてよく,この二つの合成(Aの分が先)は,
と書いてよく,この二つの合成(Aの分が先)は,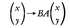 となって,行列の積BAに対応する。
となって,行列の積BAに対応する。
転置行列
Aが(m,n)行列であるとき,Aの(i,j)成分を(j,i)成分とすることによって得られる(n,m)行列をAの転置行列という。tAで表すのがふつうである。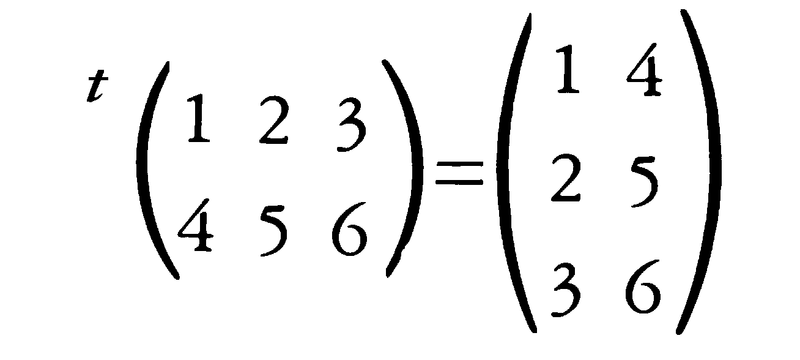
A,Bが同じ型の行列ならば,
t(A+B)=tA+tB
A,Cの積が定義される場合は,
t(AC)=(tC)(tA) (順序に注意)
逆行列
n次正方行列A,Bについて,ABが単位行列Iになるときは,BAもIになる。このとき,BはAの逆行列であるといい,A⁻1で表す。正方行列Aは必ずしも逆行列をもつとは限らない。Aが逆行列をもつとき,Aは正則行列であるといい,このとき逆行列はただ一つ定まる。また(A⁻1)⁻1=Aである。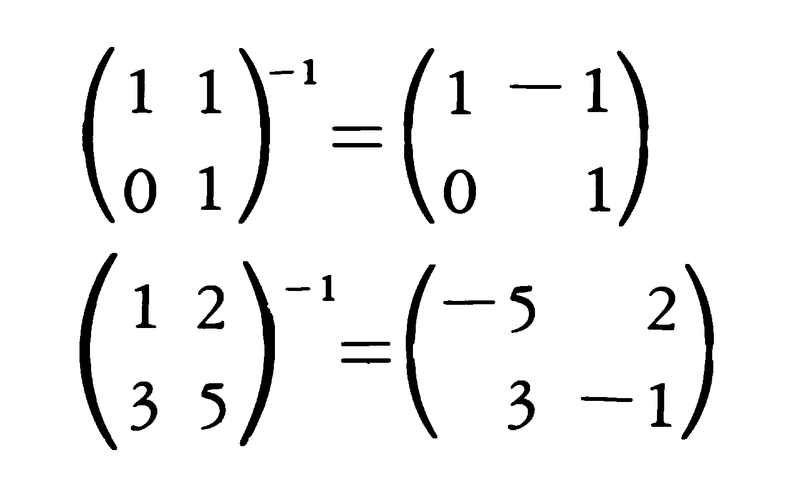
行列式を利用すれば次のことがいえる。n次正方行列Aが逆行列をもてば,Aの行列式|A|は0ではない。逆に|A|が0でないときは,逆行列は次のようにして得られる。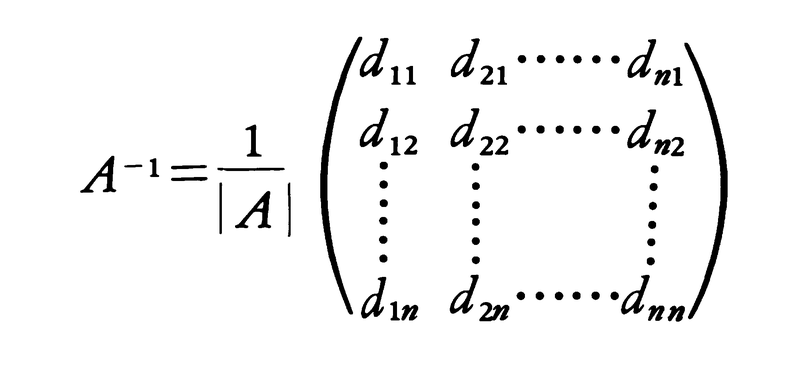
ただし,dijは行列Aから第i行と第j列を除いて得られたn-1次正方行列Aijの行列式の(-1)i⁺j倍である。このdijを(j,i)成分とする行列をAの余因子行列という。これをDで表せば,
DA=AD=|A|I (Iはn次単位行列)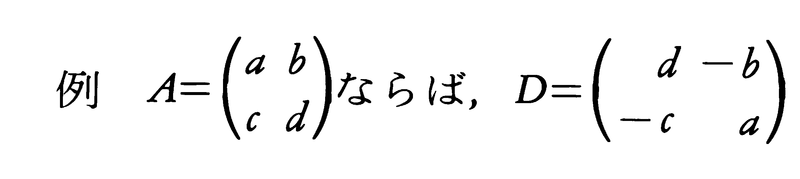
行列の階数
ここで述べることは,一つの(m,n)行列Aに対して,その成分を含む体Kをどうとっても結果が同じであることにまず注意しておく。Aで定まる一次変換,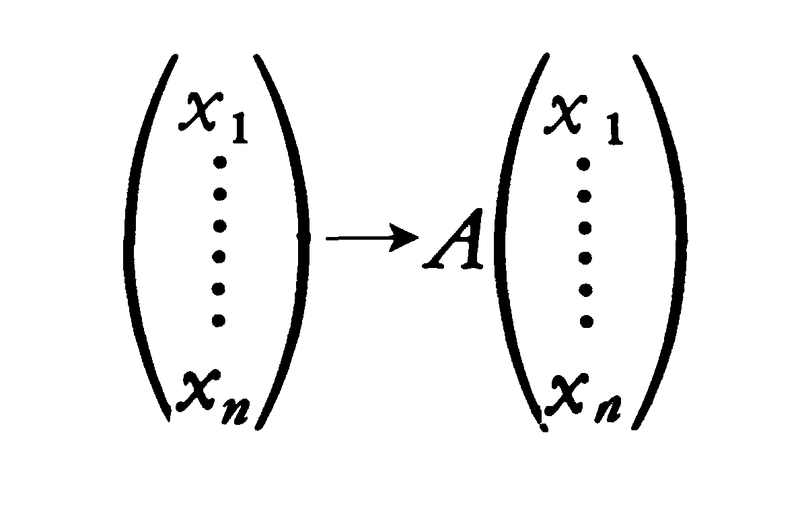
はK上のn次元ベクトル空間からm次元ベクトル空間の中への写像を与え,像全体Wは部分ベクトル空間になる。Wの次元をAの階数という。
(1)Aのm個の行ベクトルのうち一次独立なものの最大数,Aのn個の列ベクトルのうち一次独立なものの最大数は,いずれも階数に等しい。Aの階数はtAの階数と等しい。
(2)m,nどちらよりも大きくないような自然数rに対して,Aの行,列をr個ずつ選んでできるr次正方行列を総称してAのr次の小行列という。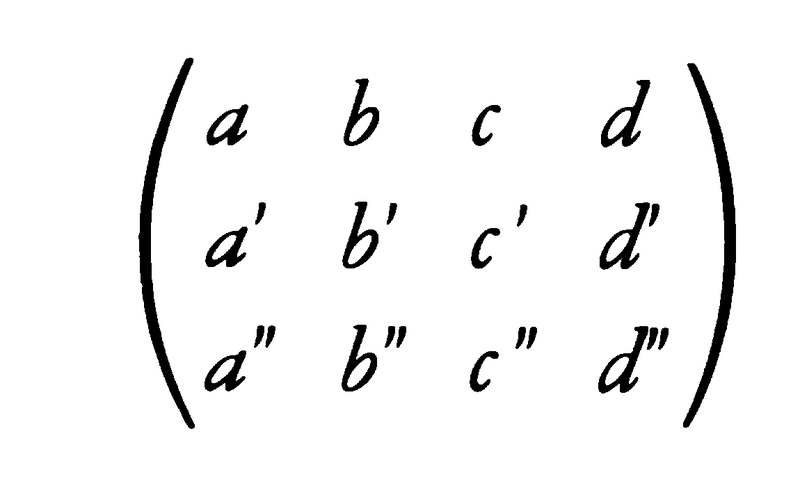
の二次の小行列は,
のように,合計3C2×4C2=18個できる。
Aの階数rは,〈Aのr次小行列のうちにその行列式が0でないものがあり〉〈r+1次の小行列でその行列式が0でないものは存在しない〉ということでも特徴づけられる。
固有多項式
Aがn次正方行列であるとき,n次の単位行列Iと変数xを考えて,行列xI-Aの行列式を作ると,これは,xn+c1xn⁻1+……+cnの形になる。この多項式をAの固有多項式という。このとき,
An+c1An⁻1+……+cn-1A+cnI=0
(零行列)となる。この結論は,ケーリー=ハミルトンの定理Cayley-Hamilton's theoremと呼ばれる。cn=(-1)n×(Aの行列式)であり,Aの(i,j)成分をaijとすると,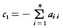 である。
である。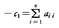 をAのトレースtraceという。
をAのトレースtraceという。
Aが正則なのは,cn≠0のときで,このとき,
A⁻1=-cn⁻1(An⁻1+c1An⁻2+……+cn-2A+cn-1I)
であるから,上の結果は逆行列の計算にも利用できる。
正方行列においては,(i,i)成分の位置を総称して対角線という。対角線以外の場所の成分が全部0の正方行列を対角型の行列という。対角線より下(または上)の場所の成分が0の正方行列を上半(下半)三角行列,総称して単に三角行列という。tA=Aとなるとき,Aは対称行列であるという。実行列で,tA=A⁻1であるものを直交行列という。二次の直交行列は,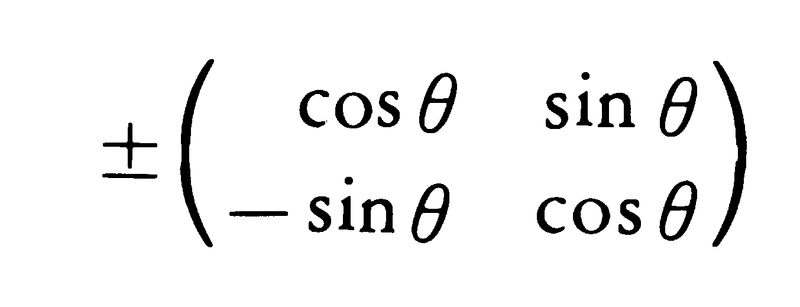
であり,+のほうは平面における原点のまわりの回転を表す。
Aが複素行列であるとき,各成分をその複素共役に置き換えた行列を,行列Aの複素共役といい,Āで示すことにしよう。Āの転置行列A*=tĀがAの逆行列になるとき,Aはユニタリ行列であるという。A*=AのときAはエルミート行列であるという。
執筆者:永田 雅宜
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「行列」の意味・わかりやすい解説
行列
ぎょうれつ
matrix
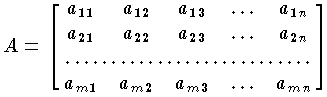 を mn 行列,または m×n 行列,あるいは m 行 n 列の行列という。すなわち,要素の横の並びを行 row,縦の並びを列 columnという。この行列 A を簡単に (aij)(i=1,2,…,m;j=1,2,…,n) と書く。線形写像
を mn 行列,または m×n 行列,あるいは m 行 n 列の行列という。すなわち,要素の横の並びを行 row,縦の並びを列 columnという。この行列 A を簡単に (aij)(i=1,2,…,m;j=1,2,…,n) と書く。線形写像 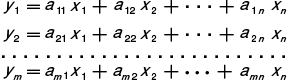 を,ベクトルでまとめて
を,ベクトルでまとめて 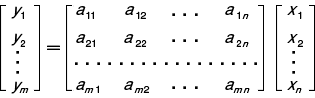 さらには y=Ax と書くのに用い,それに合せて和や積を定義する。 aij をこの行列の ij 要素という。特に m=n の場合を n 次の行列 (正方行列) という。2つの行列の和と積に関して,結合および分配の法則は成り立つが,交換の法則は和については成り立ち,積については成り立たない。
さらには y=Ax と書くのに用い,それに合せて和や積を定義する。 aij をこの行列の ij 要素という。特に m=n の場合を n 次の行列 (正方行列) という。2つの行列の和と積に関して,結合および分配の法則は成り立つが,交換の法則は和については成り立ち,積については成り立たない。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「行列」の意味・わかりやすい解説
行列【ぎょうれつ】
→関連項目代数学|マトリックス力学
出典 株式会社平凡社百科事典マイペディアについて 情報
普及版 字通 「行列」の読み・字形・画数・意味
【行列】こうれつ・ぎようれつ
字通「行」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
世界大百科事典(旧版)内の行列の言及
【行列式】より
…英語ではdeterminantといい,これは決定因子という意味の言葉であり,一次連立方程式の解を決めるのに重要なものということで名付けられたという。明治の日本では当初デテルミナントといったが,後にdeterminantの訳を行列式,matrixの訳を行列とするのが定着した。
[定義]
行列式は正方行列に対して定義され,|A|,det Aなどの記号が用いられる。…
【金属組織】より
…したがって亜共析鋼の標準組織は初析フェライトとパーライトの二つの要素を含んでいるとみなしてもよい。 合金の体積の大部分を占める組織構成要素をマトリックスmatrixといい,マトリックスを構成している相をマトリックス相という。マトリックスの中に分散している組織構成要素は介在物あるいは分散物と呼ばれ,これを構成している相を分散相あるいは第2相と呼んでいる。…
【紙型】より
…一つの活版組版と同じもの(鉛版)を多数作るとき用いる紙製の雌型。通常,紙型用紙といわれる材料を組版の上にのせて圧力を加えて作る。湿式紙型(ウェットマットwet mat)と乾式紙型(ドライマットdry mat)とがあり,前者は乾燥しないように保存された紙型用紙を活版組版の上にのせ剛毛の打ち刷毛(はけ)でたたいて作るので〈たたき〉とも呼ばれる。現在,乾式紙型が多用される。乾式紙型は数十層を抄き合わせた特殊なドライマット原紙という厚紙をあらかじめ湿して軟らかくし,プレスで活版組版に押しつけて成形する。…
※「行列」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
[名](スル)1 人から受けた礼・贈り物に対して行為や品物で報いること。また、その行為や品物。「地酒を贈って返礼する」2 仕返しをすること。また、その仕返し。意趣返し。返報。[補説]書名別項。→返礼[...