世界大百科事典（旧版）内のウィーナー規範の言及
【フィルター】より
…言い換えると，過去に得られた測定データy(t)(τ≦t)からの線形でかつ因果的な作用素として積分，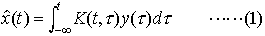
を考えるのだが，誤差の2乗平均e2(t)＝(
(t)－x(t))2の平均値を最小にするような核関数K(t，τ)を決めることを考えた。このように，誤差の2乗平均を最小にすることをr.m.s.規範あるいはウィーナー規範ともいい，このこととx(t)とn(t)の定常ガウス性を仮定することにより，この最適フィルターの問題が周波数領域できれいに解けることを示した。すなわち，定常性から核関数はK(t，τ)＝K(t－τ)のように1個のパラメーターで表現でき，これを利用して，(1)式のスペクトル表現を導き，最適フィルターの核関数のラプラス変換，
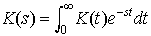がx(t)とn(t)のスペクトル関数表現から求められることを示した。…
※「ウィーナー規範」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponsored by 