世界大百科事典（旧版）内のコーシーの平均値の定理の言及
【微分】より
…例えばf(x)＝x3についてはf′(0)＝0であるがy＝f(x)のグラフは図4のようになり，f(0)は極大でも極小でもない。 次の定理は平均値の定理の一般化で，コーシーの平均値の定理と呼ばれている。f(x)，g(x)が閉区間[a,b]で連続，開区間(a,b)で微分可能でg′(x)≠0ならば，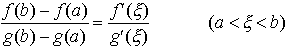
を満たすξが存在する。…
【平均値の定理】より
…微積分学において有用な定理の一群。
［微分法における平均値の定理］
(1)関数f(x)がa≦x≦bで連続，a＜x＜bで微分可能ならば，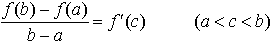
となるcが存在する。(2)f(x)，g(x)が上記(1)のfと同じ仮定を満たし，さらにa＜x＜bにおいてg′(x)≠0ならば，
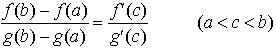となるcが存在する。(1)，(2)をそれぞれラグランジュの平均値定理，コーシーの平均値定理というが，単に平均値定理といえば(1)を指す。(2)でg(x)≡xの場合が(1)であり，(1)でさらにf(b)＝f(a)の場合はロルの定理と呼ばれる。…
※「コーシーの平均値の定理」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponserd by 