世界大百科事典（旧版）内のシャウダー,J.P.の言及
【関数解析学】より
…(b)(1)が0以外の解xをもつ場合は，その解の中で線形独立なものは有限個であり，そのとき(2)が解をもつための条件は，λf－T*f＝0なる任意のf∈X*に対してf(u)＝0なることである。これは，リース=シャウダーの択一定理と呼ばれ，積分方程式，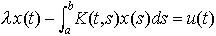
にあてはめると，すなわち，
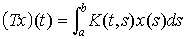なる作用素Tを考えると，フレドホルムの択一定理が得られる。
［非線形問題］
常微分方程式の初期値問題， x′＝f(t,x)，x(0)＝a ……(3) は，未知関数x(t)に関する積分方程式，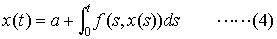
と同等である。…
【不動点定理】より
…〈Xがn次元ユークリッド空間の有界閉集合ならば，XからX自身へのどんな連続写像も不動点をもつ〉。この定理はS.レフシェッツによってXが有限多面体の場合に(1926)，また，J.P.シャウダーによってXがバナッハ空間の凸閉集合の場合に(1930)拡張された。とくに，レフシェッツは有限多面体からそれ自身への連続写像fに対し，ホモロジー群を用いて今日レフシェッツ数と呼ばれている整数を定義し，これがfの不動点の代数的個数と一致すること，したがってfのレフシェッツ数が0でなければfは不動点をもつことを示した。…
※「シャウダー,J.P.」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponserd by 