世界大百科事典（旧版）内のタウバー型定理の言及
【フーリエ解析】より
…(a)f(t)が(3′)の形に表されるためには，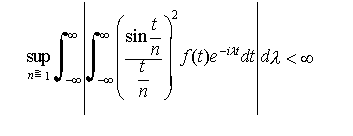
となることが必要かつ十分である。(b)(3′)のfに対し，任意のλ0において，
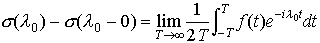とくにσ(λ)がλ＝λ0－δおよびλ＝λ0＋δ(δ＞0)において連続ならば，
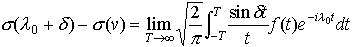(c)(3′)において有界変動関数σ(λ)の不連続点をλ1，λ2，……とし，σn＝σ(λn)－σ(λn－0)(n＝1,2，……)とすると，
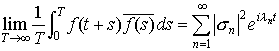フーリエ解析はN.ウィーナーによってタウバー型定理にも応用された。タウバー型定理とは，べき級数に関するアーベルの定理の逆に当たるもので，収束半径が1のべき級数
anznにおいて，an＝0(1/n)であって，
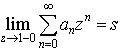が存在するならば，
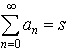となるという定理である。…
※「タウバー型定理」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponsored by 