ハンケルの公式（読み）はんけるのこうしき

世界大百科事典（旧版）内のハンケルの公式の言及

【ベッセル関数】より

…νを任意の複素数とするとき，2階の線形常微分方程式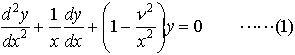，をベッセルの微分方程式という。νが整数(0，±1，±2，……)でないときは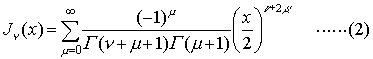，は0＜｜x｜＜∞で収束し，(1)の解となる(Γ(ν)はΓ関数)。これを第1種ベッセル関数または円柱関数という。ここでJ_ν(x)とJ_－ν(x)とは一次独立である。νが0または正の整数nのときも(2)は(1)の解であり，(2)の右辺の級数は｜x｜＜∞で収束する。この場合，(2)のνを－νでおきかえてから形式的にν→nとして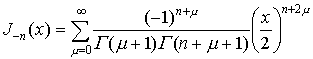，と定義するが，J_n(x)＝(－1)ⁿJ_－n(x)なる関係があるから，J_n(x)とJ_－n(x)とは一次独立でない。…

※「ハンケルの公式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」