世界大百科事典（旧版）内のブラドワディーンの関数の言及
【ブラドワディーン】より
…また科学史上の貢献は，《運動における速さの比について》(1328)によって不滅である。中世数学の比例論とくに比の合成の概念に依拠して，アリストテレスの運動規則をより整合的に定式化する試みをなし，現代的に記号化すれば，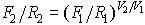
なる関係を提示した(〈ブラドワディーンの関数〉と称される。ただし，Fは力，Rは抵抗，Vは速さ)。…
※「ブラドワディーンの関数」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponserd by 