世界大百科事典（旧版）内のヘルグロッツの定理の言及
【フーリエ解析】より
…数列｛an｜－∞＜n＜∞｝において，任意のnと任意の複素数α1，α2，……，αnに対して，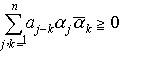
となるとき，｛an｝を正の定符号数列または正型数列という。正の定符号数列｛an｝は，[－π，π]上の単調増加右連続関数σ(λ)でσ(－π)＝0なるものにより，
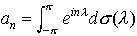と一意的に表される(ヘルグロッツの定理)。逆にこの式で与えられる数列｛an｝は正の定符号数列である。…
※「ヘルグロッツの定理」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponsored by 