世界大百科事典（旧版）内のボルテラ型積分方程式の言及
【積分方程式】より
…しかし積分方程式を系統的に論じたのは，ボルテラV.Volterra(1860‐1940)とフレドホルムE.I.Fredholm(1866‐1927)である。 一般的な形として，f(x)，K(x,y)を既知関数，φ(x)を未知関数とするとき，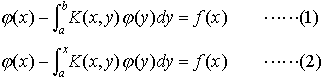
はそれぞれフレドホルム型積分方程式，ボルテラ型積分方程式と呼ばれ，K(x,y)をこれらの方程式の核という。K1(x,y)＝K(x,y)とおき，
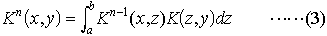n＞1で定義したKn(x,y)を反復核という。…
【逐次近似法】より
…方程式を解くに当たって，最初一つの近似解を推定し，次にこの近似解を用いてさらに精度のよい近似解を求め，逐次この操作を繰り返して近似の精度を高める方法を逐次近似法という。この操作を無限に繰り返したとき近似解が一つの極限に収束するならば，それは実際の解になる。したがってこの方法を用いて解の存在を証明することができるし，また数値解法の手段としても利用できる。 常微分方程式x′＝f(t,x)において，t＝aでx＝bとなる解をx(t)とすれば，これは積分方程式，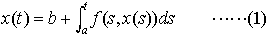
を満足する。…
※「ボルテラ型積分方程式」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」