ヤコビの行列式（読み）やこびのぎょうれつしき

世界大百科事典（旧版）内のヤコビの行列式の言及

【座標】より

…　より一般な(必ずしも一次ではない)座標変換(1)においても上に述べた群の性質が備わっている。その場合，(3)のdetAに相当するものは変換関数x_i(x′)から作られるヤコビの行列式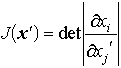，であり，これが0でなければ逆変換x_i′＝x_i′(x)が求められる。J(x′)は座標変数x_iでの積分をx_i′での積分で表すための体積要素間の関係dx₁……dx_n＝J(x′)dx₁′……dx_n′にしばしば現れる。…

【積分】より

…x＝φ(u,v)，y＝ψ(u,v)により，uv平面上の点集合Bからxy平面上の点集合Aへの1対1の写像が与えられていて，φ，ψはu,vに関して連続偏微分可能とする。このとき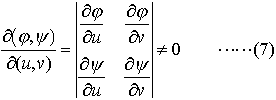，とすると，A,Bのうち一方が面積確定なら他方も面積確定で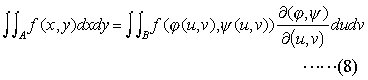，(7)の行列式を関数行列式，またはヤコビの行列式(ヤコビアンJacobian)という。とくに，x＝rcosθ,y＝rsinθ(二次元の極座標)とすると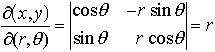，であるから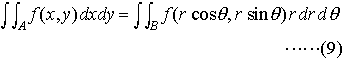，　三次元の場合にはx＝φ(u,v,w)，y＝ψ(u,v,w)，z＝χ(u,v,w)について上と同様な仮定のもとに，関数行列式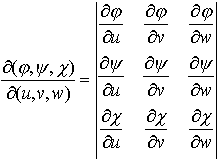，を用いて(8)と同様な公式を書くことができる。…

【置換積分法】より

…定積分の場合は，φ(t)が区間α≦t≦βで微分可能な増加関数であって，φ′(t)がこの区間で積分可能ならば，a＝φ(α)，b＝φ(β)とするとき，a≦x≦bで積分可能な関数f(x)に対して次の公式が成立する。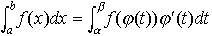　2変数の関数の場合は，適当な滑らかさの条件を満たす関数x＝φ(u,v)，y＝ψ(u,v)によって，(x,y)平面の領域Aと(u,v)平面の領域Bとが1対1に対応するならば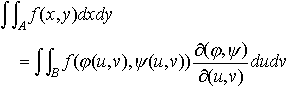，ここに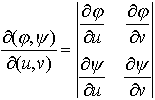，であって，この行列式はφ，ψのu,vに関する関数行列式，またはヤコビの行列式と呼ばれる。例えばA＝｛(x,y)｜x²＋y²＜a²｝のとき，x＝rcosθ,y＝rsinθによって直交座標(x,y)を極座標(r，θ)で置換すると，AはB＝｛(r，θ)｜0≦r≦a,0≦θ＜2π｝に1対1に写され，関数行列式＝rとなり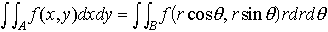，となる。…

※「ヤコビの行列式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」