ルベーグ測度（読み）るべーぐそくど

世界大百科事典（旧版）内のルベーグ測度の言及

【実関数論】より

…彼は直線上の図形の長さ，平面図形の面積，空間図形の体積の概念を，できるだけ一般な図形の範囲に拡張することを考え，測度という概念を導入し，それをもとにして積分の理論を展開した。この測度が彼の名を冠して呼ばれるルベーグ測度であり，ルベーグ測度をもとにして構成される積分がルベーグ積分である。ルベーグ積分はリーマン積分の拡張であるばかりでなく，リーマン積分と比べて多くの利点がある。…

【ルベーグ積分】より

…集合E⊂Rⁿを区間の可算無限列｛I_ν｝でおおい，そのようなあらゆるおおい方に対する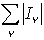の下限をm^*(E)と書いて，Eの外測度という。任意の集合A⊂Rⁿに対して，　m^*(A)＝m^*(A∩E)＋m^*(A╲E)となるときEは可測(ルベーグ可測)であるといい，m^*(E)を単にm(E)と書いてEの測度，またはルベーグ測度という。可算無限個の集合E₁,E₂，……，E_n，……が可測ならばそれらの和集合も可測であり，とくに｛E_ν｝がどの二つも互いに交わらないならば，可算加法性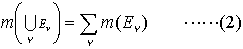，が成り立つ。…

※「ルベーグ測度」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」