コーシー＝シュワルツの不等式（読み）コーシーシュワルツのふとうしき

ブリタニカ国際大百科事典 小項目事典

コーシー＝シュワルツの不等式
コーシーシュワルツのふとうしき

「シュワルツの不等式」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のコーシー＝シュワルツの不等式の言及

【絶対不等式】より

…平面上の二つのベクトルa＝(a₁,a₂)，b＝(b₁,b₂)のなす角をθとすると，cosθ＝(a，b)/｜a｜･｜b｜(分子はベクトルの内積，分母はベクトルの長さの積)だから，｜cosθ｜≦1なることにより次の不等式が得られる。　(a₁b₁＋a₂b₂)²≦(a₁²＋a₂²)(b₁²＋b₂²)n次元のベクトルについても，同様にして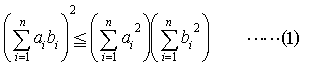，これをコーシー=シュワルツの不等式という。また，ベクトルの長さに関してよく知られた関係｜a＋b｜≦｜a｜＋｜b｜を成分で表したものをn次元のベクトルについて書けば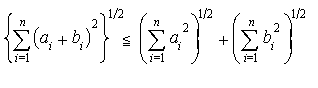，さらに一般に，任意のp≧1に対して，不等式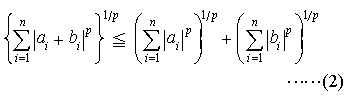，が成立する。…

※「コーシー＝シュワルツの不等式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」