ブリタニカ国際大百科事典 小項目事典 の解説
コーシー=シュワルツの不等式
コーシーシュワルツのふとうしき
「シュワルツの不等式」のページをご覧ください。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
「シュワルツの不等式」のページをご覧ください。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
…平面上の二つのベクトルa=(a1,a2),b=(b1,b2)のなす角をθとすると,cosθ=(a,b)/|a|・|b|(分子はベクトルの内積,分母はベクトルの長さの積)だから,|cosθ|≦1なることにより次の不等式が得られる。 (a1b1+a2b2)2≦(a12+a22)(b12+b22)n次元のベクトルについても,同様にして,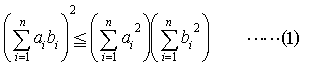 これをコーシー=シュワルツの不等式という。また,ベクトルの長さに関してよく知られた関係|a+b|≦|a|+|b|を成分で表したものをn次元のベクトルについて書けば,
これをコーシー=シュワルツの不等式という。また,ベクトルの長さに関してよく知られた関係|a+b|≦|a|+|b|を成分で表したものをn次元のベクトルについて書けば,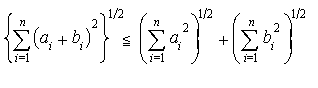 さらに一般に,任意のp≧1に対して,不等式,
さらに一般に,任意のp≧1に対して,不等式,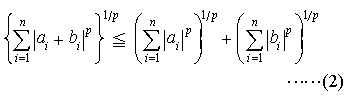 が成立する。…
が成立する。…
※「コーシー=シュワルツの不等式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
目次 飼養文化 北アメリカ 北方ユーラシア偶蹄目シカ科の哺乳類。北アメリカでは野生種はカリブーcaribouと呼ばれる。角が雄だけでなく雌にもふつうある。体長130~220cm,尾長7~20cm,...