世界大百科事典(旧版)内のパーセバルの等式の言及
【フーリエ解析】より
…一般に(2)が成立するとき,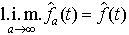 と書いて
と書いて![]() aは
aは![]() に平均収束するという(記号l.i.m.はlimit in meanと読む)。またこのとき,もとの関数fが
に平均収束するという(記号l.i.m.はlimit in meanと読む)。またこのとき,もとの関数fが![]() を使って,
を使って,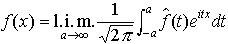 と表され(プランシュレルの定理),パーセバルの等式,
と表され(プランシュレルの定理),パーセバルの等式,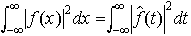 が成立する。fが有限区間(-π,π)上で2乗可積分な関数のとき,上の事実に対応して次のことがいえる。…
が成立する。fが有限区間(-π,π)上で2乗可積分な関数のとき,上の事実に対応して次のことがいえる。…
【フーリエ級数】より
…フーリエ級数がどのような意味でもとのf(x)を表しているかが問題である。f(x)が(-π,π)で2乗可積分であれば,(1)で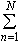 とした部分和,または(2)で
とした部分和,または(2)で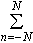 とした部分和をsN(x)とすると,
とした部分和をsN(x)とすると,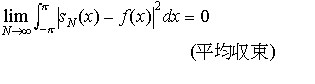 という意味でsn(x)はf(x)に近づき,このときパーセバルの等式,
という意味でsn(x)はf(x)に近づき,このときパーセバルの等式,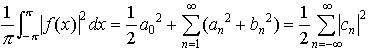 が成立する。f(x)が(-π,π)で有界変動ならば,そのフーリエ級数は,
が成立する。f(x)が(-π,π)で有界変動ならば,そのフーリエ級数は,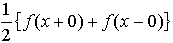 に収束する。…
に収束する。…
【フーリエ積分】より
…この事実をプランシュレルの定理という。さらにパーセバルの等式,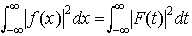 が成立する。fとその導関数f′が可積分のとき,fのフーリエ変換をF(t)とすると,f′のフーリエ変換は-itF(t)になる。…
が成立する。fとその導関数f′が可積分のとき,fのフーリエ変換をF(t)とすると,f′のフーリエ変換は-itF(t)になる。…
※「パーセバルの等式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」

