世界大百科事典（旧版）内のルジャンドル多項式の言及
【球関数】より
…それらはまた球面上のラプラシアン，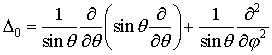
の固有関数として， Δ0Yn(θ，φ)＝－n(n＋1)Yn(θ，φ)のように特徴づけられる。 ルジャンドル多項式Pn(x)(n≧0，｜x｜≦1)も特殊関数の一種で，次の式で定められる。
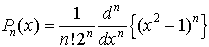これはn次多項式で微分方程式，
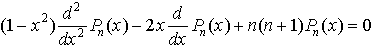を満たす。…
【ルジャンドル関数】より
…nを0または正の整数とするとき，2階の線形微分方程式，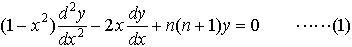
をルジャンドルの微分方程式といい，その解を一般にn次のルジャンドル関数という。また，mを正の整数とするとき，(1)を拡張して得られる常微分方程式，
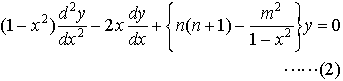をルジャンドルの陪微分方程式といい，その解をルジャンドルの陪関数という(上の各微分方程式およびそれぞれの解となる関数は，nとmを任意の複素数としても定義されているが，本項目では，nとmは整数でn≧0,m＞0として述べる)。…
※「ルジャンドル多項式」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」