世界大百科事典(旧版)内の一般化座標の言及
【解析力学】より
…18世紀後半から19世紀にかけてJ.ラグランジュ,W.ハミルトン,K.ヤコービらによって展開,確立され,相対性理論,統計力学,量子力学に対しそれらの理論構成に基本的な寄与を果たした。
[力学系の自由度と一般化座標]
簡単な例として,質量m,電荷eの1個の荷電粒子に対する運動方程式,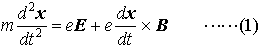 を考えると(xは粒子の位置ベクトル,tは時間,Eは電場,Bは磁場),これは粒子が電磁場(E,B)の力を受けて一定の初期条件のもとに空間の中で描く軌道を決定する。この場合,この力学系の自由度fは空間の次元数3である。…
を考えると(xは粒子の位置ベクトル,tは時間,Eは電場,Bは磁場),これは粒子が電磁場(E,B)の力を受けて一定の初期条件のもとに空間の中で描く軌道を決定する。この場合,この力学系の自由度fは空間の次元数3である。…
【座標】より
…回転系でみたときの速度d′x/dtに関係する力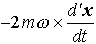 がコリオリの力と呼ばれるものであり,また-mω×(ω×x)は遠心力である。
がコリオリの力と呼ばれるものであり,また-mω×(ω×x)は遠心力である。
[解析力学における一般化座標]
質点の運動を記述するのには,その位置を表す変数と同時に速度または運動量が独立な変数として必要であるが,これは運動方程式が時間に関する2階の常微分方程式であることに起因している。前述のような座標変換を行った場合,当然ながら運動量も変換を受けることになり,変換の形式は両方を総合的に扱うことによりもっとも一般的となる。…
【自由度】より
…二つの原子A,Bが結合した2原子分子なら,xA,yA,zA,xB,yB,zBを用いてもよいし,重心の座標X,Y,ZとABの距離l,分子軸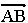 の方向を示す二つの角θ,φの計6個を用いてもよい。このような,力学系の配置や運動状態を示すのに必要な座標あるいは変数(一般化座標という)の数を自由度という。したがって2原子分子の自由度は6,平面運動する質点の自由度は2である。…
の方向を示す二つの角θ,φの計6個を用いてもよい。このような,力学系の配置や運動状態を示すのに必要な座標あるいは変数(一般化座標という)の数を自由度という。したがって2原子分子の自由度は6,平面運動する質点の自由度は2である。…
※「一般化座標」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」

