世界大百科事典（旧版）内の伊藤公式の言及
【確率微分方程式】より
…
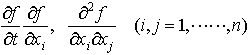がすべて有界連続関数となる有界なfに対し，X(t)が上記方程式の解であるとき，f(X(t)，t)は次の確率微分方程式を満たす。
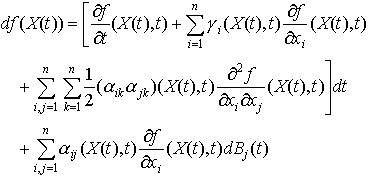これはfを形式的にテーラー展開して，dBi(t)dBj(t)＝dt(i＝jのとき)，dBi(t)dBj(t)＝0(i≠jのとき)として得られるが，伊藤公式と呼ばれ基本公式になっている。【西尾 真喜子】。…
※「伊藤公式」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponsored by 