原始帰納的関数（読み）げんしきのうてきかんすう

世界大百科事典（旧版）内の原始帰納的関数の言及

【帰納的関数】より

…〈実際effectiveに計算可能な関数〉に関する数学的概念であるリカーシブ関数recursive functionに対して，日本で定着している術語。1931年，K.ゲーデルが原始帰納的関数として初めて定式化し，これを用いて不完全性定理の証明を得た。自然数｛0,1,2，……｝の上で定義され，自然数を値とする関数f(x₁，……，x_n)が，　f(x)＝x＋1　　……(1)　　f(x₁，……，x_n)＝q　(qは定数)　　……(2)　　f(x₁，……，x_n)＝x_i　(1≦i≦n)　　……(3)　　f(x₁，……，x_n)＝g(h₁(x₁，……，x_n)，……，　　h_m(x₁，……，x_n))　　……(4)　　(ここで，gはm変数の関数で，g,h₁，……，　　h_mはすでに与えられた関数)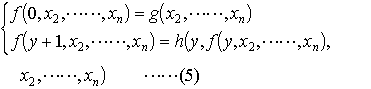　(ここで，g,hはすでに与えられた関数で，　　n＝1のときg(　)は定数を表すものとする)を有限回適用して定義されるとき，原始帰納的関数primitive recursive functionという。…

※「原始帰納的関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」