世界大百科事典(旧版)内の局所リプシッツ条件の言及
【微分方程式】より
… f1,……,fnが(t,x1,……,xn)を座標とするn+1次元空間内の開集合Gにおいて定義され,そこで連続なときには,任意の(t0,x10,……,xn0)∈Gに対し(2)を満たす解x1=x1(t),x2=x2(t),……,xn=xn(t)はつねに存在する。さらにf1,……,fnがGにおいて局所リプシッツ条件,すなわち〈KをG内の任意の有界閉集合とするとき,定数LK>0が存在して(t,x1,……,xn)∈K,(t,x1′,……,xn′)∈Kならば,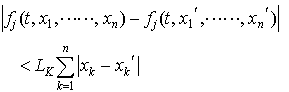 が成り立つならばそのような解はただ一つに限る。解は開区間(α,ω)で定義されるが,その定義域は一般に初期条件に依存する。…
が成り立つならばそのような解はただ一つに限る。解は開区間(α,ω)で定義されるが,その定義域は一般に初期条件に依存する。…
※「局所リプシッツ条件」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」

