正準交換関係（読み）せいじゅんこうかんかんけい

世界大百科事典（旧版）内の正準交換関係の言及

【交換関係】より

…交換子が0であるとき，AとBは交換可能であるという。もっとも重要な交換関係は，座標と運動量との間の正準交換関係であり，粒子の座標を(x,y,z)，運動量を(p_x,p_y,p_z)としたとき，[x,p_x]＝iħ/2π，[y,p_y]＝iħ/2π，……，[x,y]＝0，[p_x,p_y]＝0，……が成立する(ただしħはプランク定数をhとしてh/2πである)。これらの関係式によって種々の物理量の関係が規定される。…

【量子力学】より

…(1)その演算子の固有値がすべて実数になる，(2)その演算子の固有関数が任意のψ_tを展開できるだけ十分にたくさんある(完全系をつくる)こと。
［正準交換関係］
　一般に二つの演算子の積はその順序によって働きが違う。たとえば，位置座標と運動量の演算子の場合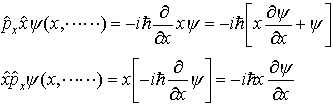，となり，演算の結果に，　(_x－_x)ψ＝－iħψだけの差がでる。…

※「正準交換関係」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」