正準運動方程式（読み）せいじゅんうんどうほうていしき

世界大百科事典（旧版）内の正準運動方程式の言及

【解析力学】より

…このq₁,q₂，……，q_fを一般化座標と呼び，一般化座標を用いて論ぜられるのが解析力学の特徴である。座標
［正準運動方程式］
　現代の物理でいう力学系とは広義概念の運動方程式　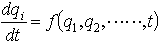に従う体系を指すことが多いが，解析力学ではその特別な場合，すなわち時間の2階常微分方程式を備えている場合に限定される。(1)において右辺の電磁場が時間変数tを座標を通して以外直接含まぬ場合(このとき(1)の力学系は自律系と呼ばれる)，tを－tに，Bを－Bに変えても方程式は不変である。…

【ハミルトン関数】より

…通常正準座標q₁,q₂，……，q_fとそれに対する正準運動量p₁,p₂，……，p_fおよび時間tの2f＋1個の独立変数の関数としてH(p₁……p_f,q₁……q_f,t)のように表されるものをハミルトン関数という。運動法則はこれを用いることにより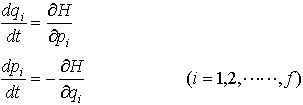，と書き表される(この方程式を正準運動方程式，あるいは単に正準方程式という)。例えば質点mの一方向の運動方程式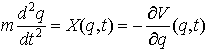，は，ハミルトン関数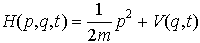，から正準方程式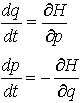，によって導かれることを見るのは容易である。…

※「正準運動方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」