世界大百科事典（旧版）内の集合算の言及
【集合】より
…(1)交換法則 A∩B＝B∩A A∪B＝B∪A(2)結合法則 (A∩B)∩C＝A∩(B∩C)＝A∩B∩C (A∪B)∪C＝A∪(B∪C)＝A∪B∪C(3)分配法則 A∩(B∪C)＝(A∩B)∪(A∩C) A∪(B∩C)＝(A∪B)∩(A∪C)(4)吸収法則 A∪(A∩B)＝A A∩(A∪B)＝A(5)ド･モルガンの法則 (A∩B)c＝Ac∪Bc (A∪B)c＝Ac∩Bcもっと一般に，Sで番号づけられた部分集合Nσについて，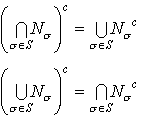
ド･モルガンの法則は，一つの集合の部分集合についての⊆，⊇，＝，∩，∪を使った関係式は，各部分集合をその補集合に置きかえ，＝はそのままにして，⊆と⊇とを取りかえ，∩と∪とを取りかえたものと同値であることを示している。これを集合算の双対性という。ここで，集合算というのは，∩，∪を集合間の演算と考えたことをいうのである。…
※「集合算」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponsored by 