世界大百科事典（旧版）内のforcingの言及
【数学基礎論】より
…ゲーデルによる簡潔にして完全な証明が《選択公理と一般連続体仮説の集合論からの無矛盾性》(1940)で与えられている。 1963年，コーエンは強制法forcingという新しい手法を発見して，V＝L，連続体仮説や選択公理がそれぞれZFC(あるいはZF)から独立であることを示す画期的な仕事を行った。実際に，コーエンは，ZFが無矛盾ならば，(1)ωの部分集合で構成可能でない集合a，すなわち，a⊂ωでa∉Lとなるような集合aが存在し，しかも一般連続体仮説(もちろんACも)が成り立つようなZFのモデルが存在する(ゲーデルの結果と合わせ考えれば，V＝LはZFに一般連続体仮説をつけ加えたものから独立)(2)選択公理は成り立つが，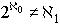
であるようなZFのモデルが存在する(したがって連続体仮説はZFCから独立)(3)ωのべき集合P(ω)がいかなる順序をつけても整列集合にはならないようなZFのモデルが存在する(したがって選択公理はZFから独立)ことなどを証明した。…
※「forcing」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」