世界大百科事典（旧版）内のHarn-Banachextensiontheoremの言及
【関数解析学】より
…線形作用素は有次元ベクトル空間に作用する行列に相当するものであり，TからT*を作る操作は，行列(aij)から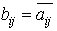
なる行列(bij)を作り出す操作に相当する。
［ハーン=バナッハの拡張定理Harn‐Banach extension theorem］
Xの線形部分空間Mがあって，ノルムから定義される距離に関して閉集合であるとする。このとき，Mで定義された有界線形汎関数f0は，X全体で定義された有界線形汎関数fに拡張され，∥f∥＝∥f0∥となる。…
※「Harn-Banachextensiontheorem」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」